คณิตศาสตร์-พื้นที่ผิวและปริมาตร

พื้นที่ผิวและปริมาตร

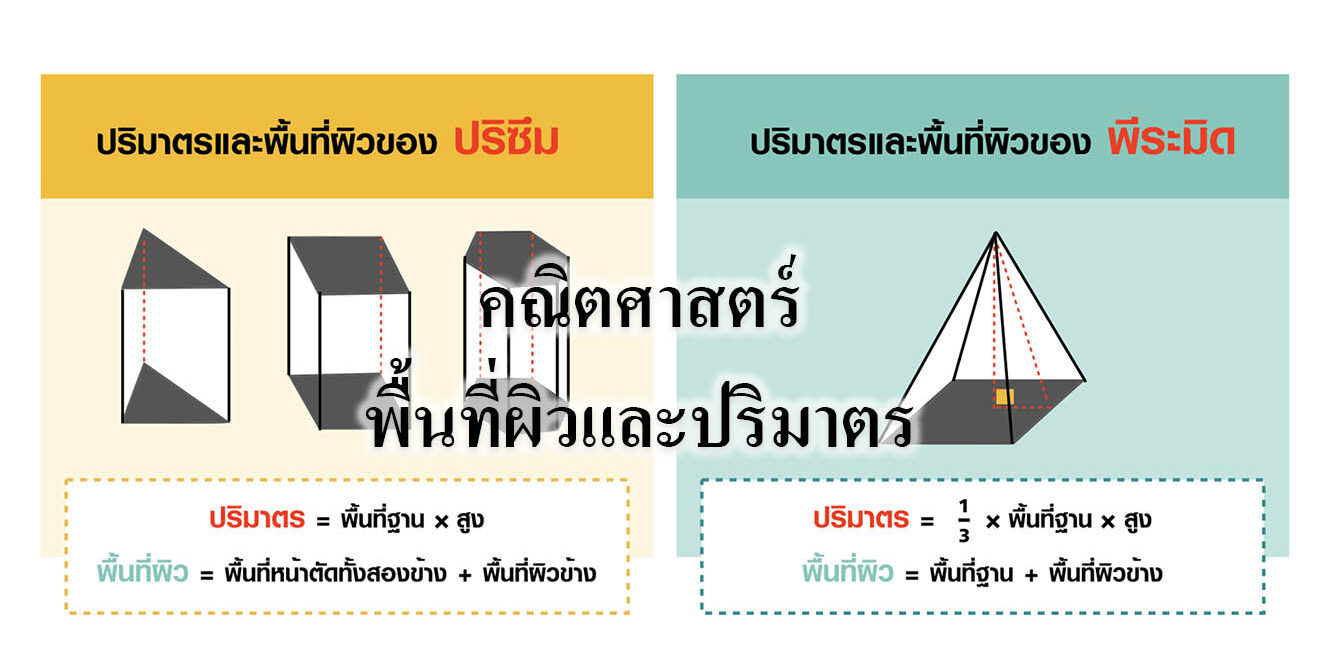
สูตรการหาพื้นที่และปริมาตร มีดังนี้

ปริซึม

   ในทางคณิตศาสตร์ ให้ความหมายคำว่า ปริซึม ดังนี้

       รูปเรขาคณิตสามมิติที่มีฐานทั้งสองเป็นรูปเหลี่ยมที่เท่ากันทุกประการ ฐานทั้งสองอยู่บนระนาบเดียวกัน และด้านข้างแต่ละด้านเป็นรูปสี่เหลี่ยมด้านขนาน หรือเรียกง่ายๆว่า แท่งเหลี่ยมตัน

   สูตรคำนวณต่างๆที่เกี่ยวกับปริซึม
ปริมาตรของปริซึม = พื้นที่ฐาน X ความสูง
พื้นที่ผิวทั้งหมดของปริซึม = พื้นที่ผิวข้าง X พื้นที่หน้าตัดหัวท้าย
พื้นที่ผิวข้างของปริซึม = ความยาวเส้นรอบฐาน X ความสูง

พีระมิด

       ในทางคณิตศาสตร์ ให้ความหมายคำว่า พีระมิด ดังนี้
รูปเรขาคณิตสามมิติที่มีฐานเป็นรูปเหลี่ยมใดๆ มียอดแหลมที่ไม่อยู่บนระนาบเดียวกันกับฐาน และหน้าทุกหน้าเป็นรูปสามเหลี่ยมที่มีจุดยอดร่วมกันที่ยอดแหลมนั้น เรียกว่า พีระมิด

สูตรคำนวณต่างๆที่เกี่ยวกับพีระมิด
พื้นที่ผิวข้างของพีระมิด = 1/2 X ความยาวรอบฐาน X สูงเอียง
= พื้นที่ของหน้าทุกหน้ารวมกัน
พื้นที่ผิวของพีระมิด = พื้นที่ผิวข้างของพีระมิด X พื้นที่ฐานของพีระมิด

ทรงกระบอก

        ในทางคณิตศาสตร์ให้ความหมายคำว่า ทรงกระบอก ดังนี้
รูปเรขาคณิตสามมิติที่มีฐานสองฐานเป็นรูปวงกลมที่เท่ากันทุกประการและอยุ่บนระนาบที่ขนานกัน และเมื่อตัดรูปเรขาคณิตสามมิตินั้นด้วยระนาบที่ขนานกับฐานแล้ว จะได้หน้าตัดเป็นวงกลมที่เท่ากันทุกประการกันฐานเสมอ เรียกรูปเรขาคณิตสามมิตินั้นว่า ทรงกระบอก

สูตรคำนวณต่างๆที่เกี่ยวกับทรงกระบอก
ปริมาตรทรงกระบอก = (22/7 หรือ 3.14) X รัศมียกกำลัง 2 X สูงตรง
พื้นที่ผิวข้างของทรงกระบอก = 2(22/7 หรือ 3.14) X รัศมี X สูงตรง + 2(22/7 หรือ 3.14) X รัศมียกกำลัง 2

ในทางคณิตศาสตร์ให้ความหมายคำว่า กรวย ดังนี้
รูปเรขาคณิตสามมิติที่มีฐานเป็นรูปวงกลม มียอดแหลมที่ไม่อยู่ในระนาบเดียวกันกับฐาน และเส้นที่ต่อระหว่างจุดยอดกับจุดใดๆ บนขอบของฐานเป็นส่วนของเส้นตรง เรียกรูปเรขาคณิตสามมิตนั้นว่า กรวย

สูตรคำนวณต่างๆที่เกี่ยวข้องกับกรวย
ปริมาตรของกรวย = 1/3 X (22/7 หรือ 3.14) X รัศมียกกำลังสอง X สูงตรง
พื้นที่ผิวของกรวย = (22/7 หรือ 3.14) X รัศมี X สูงเอียง + (22/7 หรือ 3.14) X รัศมียกกำลังสอง

ทรงกลม

       ในทางคณิตศาสตร์ให้ความหมายคำว่า ทรงกลม ดังนี้
รูปเรขาคณิตสามมิติที่มีผิวโค้งเรียบ และจุดทุกจุดบนผิวโค้งอยู่ห่างจากจุดจุดหนึ่งเป็นระยะเท่ากัน เรียกว่า ทรงกลม
จุดคงที่นั้นเรียกว่า จุดศูนย์กลางของทรงกลม
ระยะที่เท่ากันนั้นเรียกว่า รัศมีของทรงกลม

สูตรคำนวณต่างๆที่เกี่ยวข้องกับทรงกลม

ปริมาตรของทรงกลม = 4/3 X (22/7 หรือ 3.14) X รัศมียกกำลัง 3
พื้นที่ผิวของทรงกลม = 4 X (22/7 หรือ 3.14) X รัศมียกกำลัง 2

ปริซึมและพีระมิด

ทรงสามมิติ (Solid) ในที่นี้มีความหมายอย่างเดียวกับรูปทรงที่มีความกว้าง ความยาว และความสูง ทรงสามมิติที่กล่าวถึง ได้แก่
ทรงสี่เหลี่ยมมุมฉาก ปริซึม ทรงกระบอก กรวย ทรงกลม เป็นต้น

พื้นที่ผิว คือ ผลรวมของพื้นที่ผิวข้างทุกด้านของรูปทรง เช่น พื้นที่ผิวของรูปทรงสี่เหลี่ยมมุมฉากจะมีพื้นที่ผิวข้าง 6 ด้านรวมกัน
ปริมาตร คือ ปริมาณที่วัดเพื่อแสดงบริเวณที่ว่าง (ความจุ) ภายในรูปทรงสามมิติ การวัดปริมาตรของรูปทรงสามมิติใช้หน่วยวัดเป็น
ลูกบาศก์หน่วย

ปริมาตร 1 ลูกบาศก์หน่วย คือ รูปทรงสี่เหลี่ยมมุมฉากที่มีความกว้าง 1 หน่วย ความยาว 1 หน่วย และความสูง 1 หน่วย

ลูกบาศก์ A มีปริมาตร 1 ลูกบาศก์หน่วย
ลกบาศก์ B มีปริมาตร 1 ลูกบาศก์หน่วย

พื้นที่ผิวและปริมาตรรูปทรงสี่เหลี่ยมมุมฉาก 

 ทรงสี่เหลี่ยมมุมฉาก คือ รูปทรงสามมิติที่ทุกด้านเป็นรูปเหลี่ยมมุมฉาก และด้านตรงข้ามเท่ากันทุกประการและขนานกัน

สูตร พื้นที่ผิวของทรงสี่เหลี่ยมมุมฉาก = ผลรวมของด้านทั้ง 6 ด้าน
ปริมาตรของทรงสี่เหลี่ยมมุมฉาก = ความกว้าง x ความยาว x ความสูง
หรือ ปริมาตรของทรงสี่เหลี่ยมมุมฉาก = พื้นที่ฐาน x สูง

พื้นที่รูปสามเหลี่ยม เมื่อกำหนดด้านให้ 3 ด้าน 

พื้นที่รูปสามเหลี่ยมด้านเท่า

1. ปริซึม 
ปริซึม คือ ทรงสามมิติที่มีฐานทั้งสองเป็นรูปสี่เหลี่ยมที่เท่ากันทุกประการ ฐานทั้งคู่อยู่ในระนาบที่ขนานกัน และด้านข้างแต่ละด้านเป็น

 รูปสี่เหลี่ยมด้านขนาน

สูตร พื้นที่ผิวของปริซึม = พื้นที่ผิวข้าง + พื้นที่ผิวหน้าตัด
ปริมาตรปริซึม = พื้นที่ฐาน x สูง

 พื้นที่ผิวของปริซึม เมื่อคลี่ผิวข้างของปริซึมใด ๆ พบว่า จะเกิดเป็นรูปสี่เหลี่ยมผืนผ้าที่มีความยาวเท่ากับเส้นรอบฐานและส่วน

กว้างเท่ากับความสูง ดังรูป

สูตร พื้นที่ผิวข้าง = เส้นรอบฐาน x สูง

2.พีระมิด

 พีระมิด คือ ทรงสามมิติที่มีฐานเป็นรูปเหลี่ยมใด ๆ มียอดแหลม ซึ่งไม่อยู่ในระนาบเดียวกับฐานและหน้าทุกหน้าเป็นรูปสามเหลี่ยม
ที่มีจุดยอดร่วมกันที่ยอดแหลม

ลักษณะของพีระมิดตรง 
1. หน้าของพีระมิดตรงเป็นรูปสามเหลี่ยมหน้าจั่ว และเท่ากันทุกรูป
2. สันของพีระมิดตรงจะยาวเท่ากันทุกเส้น
3. ความสูงเอียงของพีระมิดตรงด้านเท่า มุมเท่า จะยาวเท่ากันทุกเส้น
4. ปริมาตรของพีระมิด เป็นหนึ่งในสามของปริมาตร ปริซึมที่มีฐานเท่ากันกับพีระมิดและมีส่วนสูงเท่ากับพีระมิด

การหาส่วนต่าง ๆ ของพีระมิด 

1. โจทย์ พีระมิดฐานสี่เหลี่ยมผืนผ้า กว้าง 10 เซนติเมตร ยาว 18 เซนติเมตร และความสูงของพีระมิดเป็น 12 เซนติเมตร จงหาความสูงเอียงทั้ง 2 ด้าน พีระมิดเป็น 12 เซนติเมตร จงหาความสูงเอียงทั้ง 2 ด้าน

(1) ความสูงเอียงด้านกว้าง

(2) ความสูงเอียงขนานด้านยาว

2. โจทย์ พีระมิดสี่เหลี่ยมผืนผ้า

กว้าง 6 เซนติเมตร ยาว 8 เซนติเมตร มีสันยาว 13 เซนติเมตร จงหาส่วนสูง

ตัวอย่าง พีระมิดแห่งหนึ่งมีฐานเป็นรูปสี่เหลี่ยมจัตุรัส ยาวด้านละ 6 เมตร สูงเอียง 5 เมตร และสูงตรง 4 เมตร จงหาพื้นที่ผิวและปริมาตรของพีระมิด

3. กรวย

ในทางคณิตศาสตร์ให้ความหมายคำว่า กรวย ดังนี้
รูปเรขาคณิตสามมิติที่มีฐานเป็นรูปวงกลม มียอดแหลมที่ไม่อยู่ในระนาบเดียวกันกับฐาน และเส้นที่ต่อระหว่างจุดยอดกับจุดใดๆ บนขอบของฐานเป็นส่วนของเส้นตรง เรียกรูปเรขาคณิตสามมิตนั้นว่า กรวย

สูตรคำนวณต่างๆที่เกี่ยวข้องกับกรวย
ปริมาตรของกรวย = 1/3 X (22/7 หรือ 3.14) X รัศมียกกำลังสอง X สูงตรง
พื้นที่ผิวของกรวย = (22/7 หรือ 3.14) X รัศมี X สูงเอียง + (22/7 หรือ 3.14) X รัศมียกกำลังสอง

กรวย (cone) คือ ทรงสามมิติใด ๆ ที่มีฐานเป็นวงกลม มียอดแหลมที่ไม่อยู่บนระแนบเดียวกันกับฐาน และเส้นที่ต่อระหว่างจุดยอดและจุดใด ๆ บนขอบของฐานเป็นส่วนของเส้นตรง

4.ทรงกระบอก

ทรงกระบอก (Cylinder) คือ ทรงสามมิติใด ๆ ที่มีฐานเป็นรูปวงกลมที่เท่ากันทุกประการกับหน้าตัด และอยู่ในระนาบที่ขนานกัน เมื่อตัดทรงสามมิตินี้ด้วยระนาบที่ขนานกับฐานแล้ว จะได้รอยตัดเป็นวงกลมที่เท่ากันทุกประการกับฐานเสมอ