รูปหลายเหลี่ยมคล้าย

รูปหลายเหลี่ยมสองรูปคล้ายกัน ก็ต่อเมื่อ รูปหลายเหลี่ยมสองรูปนั้นมี

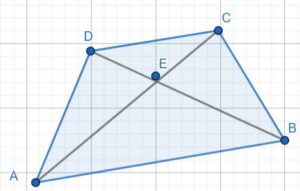
1. สี่เหลี่ยม ABCD เป็นสี่เหลี่ยมคางหมู เส้นตรง AC และ เส้นตรง BD ตัดกันที่จุด E มีสามเหลี่ยมคู่ใดบ้างที่คล้ายกัน

วิธีทำ

ให้พิจารณา สามเหลี่ยม DEC และสามเหลี่ยม AEB

1 มุม DEC = มุม AEB (มุมตรงข้าม)

2 มุม DCE = มุม EAB (มุมแย้ง)

3 มุม CDE = มุม EBA (มุมแย้ง)

ดังนั้น สามเหลี่ยม DEC คล้ายกับสามเหลี่ยม AEB เพราะมีมุมที่มีขนาดเท่ากันเป็นคู่ๆครบ 3 คู่

2. สามเหลี่ยม ABC เป็นสามเหลี่ยมมุมฉากที่มี เส้นตรง AD ตั้งฉากกับ เส้นตรง BC ที่จุด D

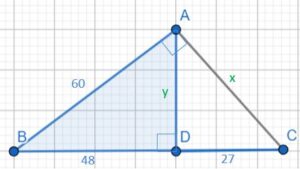
พิสูจน์ว่าแต่ละรูปสามเหลี่ยม 2 รูปคล้ายกัน คือ จะต้องมีมุทเท่ากันทั้ง 3 คู่

ΔDBA ∼ ΔABC เพราะ

1 มุม BDA = มุม BAC ( มุมฉาก 90 องศา)

2 มุม DBA = มุม ABC (มุมร่วม)

3 มุม DAB = มุม ACB (มุมภายในสามเหลี่ยมเท่ากับ 180 องศา)

ΔDAC ∼ ΔABC เพราะ

1 มุม CDA = CAB

2 มุม DCA = ACB

DAC = ABC

ΔDBA ∼ ΔDAC เพราะ

1 มุม BDA = ADC

2 มุม DAB = DCA

3 มุม ABD = CAD

ต่อมาจะหาค่า x และ y เนื่องจาก ΔDAC ∼ ΔABC

ดังนั้น AC/BC = AD/BA = CD/CA

x/75 = y/60 = 27/x

หาค่า x

x/75 = 27/x

x^2 = 75*27

x^2 = 2025

x = 45

แทน x ด้วย 45 จะได้

x/75 = y/60

45/75 = y/60

y = ( 45 * 60 ) /75

y = 36

3. ΔCAT ∼ ΔFOX ถ้า CA:AT = 2:5 และ เส้นตรง OX = 12 cm. จงหาความยาวของเส้นตรง FO

ΔCAT ∼ ΔFOX
จะได้ CA/AT = FO/OX
แต่ CA : AT = 2 : 5 และ OX = 12
จะได้ว่า
2/5 = FO/12

FO = (12 *2) /5 = 24/5
ดังนั้น FO = 4.8 cm.

-ขอบคุณข้อมูล https://www.outputmath.com/