คณิตศาสตร์เรื่อง ภาคตัดกรวย วงรี

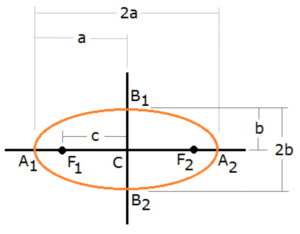
แกนที่แบ่งครึ่งรูปวงรี ได้แก่ แกนเอก (ยาว=2a) ซึ่งแสดงความยาวของวงรี
ส่วนอีกแกนเรียกว่า แกนโท (ยาว=2b) แสดงถึงความกว้างของวงรี ซึ่ง a>b เสมอ

จากรูปข้างบน ถ้าจุดกำเนิดอยู่ที่ C(h, k) จะได้พิกัดของจุดปลายแกนทั้ง 4 จุด ดังนี้

พิกัดของจุดปลายแกนเอก A1 คือ (h-a, k)

พิกัดของจุดปลายแกนเอก A2 คือ (h+a, k)

พิกัดของจุดปลายแกนโท B1 คือ (h, k+b)

พิกัดของจุดปลายแกนโท B2 คือ (h, k-b)

ข้อสังเกตวงรี:

1. สมการวงรีจะคล้ายกับวงกลม วิธีสังเกตว่าสมการนี้ใช่วงรีหรือไม่ ให้สังเกตโดย
– จัดรูปให้เป็น x² และ y² สัมประสิทธิ์หน้าทั้งสองเทอมนี้เป็นค่าบวกแต่มีค่าไม่เท่ากัน
(ตัวส่วนไม่เท่ากัน ซึ่งเป็นการขยายระยะแกนเอกและแกนโท)
– ด้านขวาของสมการเป็น 1

2. วงรีวางตัวแบบไหน ให้ดูจากแกนเอก แกนโท เพราะแกนเอกยาวกว่าแกนโทเสมอ นั่นคือ a>b เสมอ
สำหรับตัวส่วน a, b จะเป็นความยาวครึ่งหนึ่งของแกนเอก และแกนโทตามลำดับ

– ถ้า a อยู่กับ x และ b อยู่กับ y แสดงว่าแกนเอกของวงรีวางนอนขนานไปกับแกน x เหมือนในรูปตัวอย่างข้างบน

– ถ้า a อยู่กับ y และ b อยู่กับ x แสดงว่าแกนเอกของวงรีวางตั้งขึ้นขนานไปกับแกน y ดังรูปในตัวอย่างข้างล่างนี้

2) วงรีที่วางตัวในแนวแกน y (แนวตั้ง)

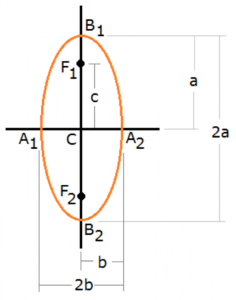
สมการวงรี: 

ระยะโฟกัส (F): 
จากรูป ถ้าจุดกำเนิดอยู่ที่ C(h, k) จะได้พิกัดของจุดปลายแกนทั้ง 4 จุด ดังนี้

พิกัดของจุดปลายแกนเอก B1 คือ (h, k+a)
พิกัดของจุดปลายแกนเอก B2 คือ (h, k-a)
พิกัดของจุดปลายแกนโท A1 คือ (h-b, k)
พิกัดของจุดปลายแกนโท A2 คือ (h+b, k)