กราฟของฟังก์ชันกำลังสอง
5.1 แนะนำฟังก์ชัน
5.2 กราฟของฟังก์ชันกำลังสอง
ฟังก์ชันกำลังสอง
ฟังก์ชันกำลังสอง (Quadratic function)
ฟังก์ชันกำลังสองเป็นฟังก์ชันที่อยู่ในรูป y = ax2 + bx + c เมื่อ a, b, c เป็นจำนวนจริงใด ๆ และ a ¹ 0 ซึ่งกราฟของฟังก์ชันกำลังสอง เรียกว่า พาราโบลา
1) y = 2x2 + 3x – 10 เมื่อ a = 2 , b = 3 และ c = -1
2) y = x2 + 1 เมื่อ a = 1 , b = 0 และ c = 1
3) y = -x2 + 2x + 1 เมื่อ a = -1 , b = 2 และ c = 1
1) กราฟของฟังก์ชันกำลังสอง ที่กำหนดด้วยสมการ y = ax2 เมื่อ a ¹ 0
กราฟของฟังก์ชันกำลังสอง มีชื่อเรียกว่า พาราโบลา ซึ่งลักษณะของกราฟของฟังก์ชันขึ้นอยู่กับค่าของ a , b และ c และเมื่อ a เป็นบวกหรือลบ จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ และกราฟของฟังก์ชันกำลังสองที่กำหนดด้วยสมการ y = ax2 เมื่อ a ¹ 0 เมื่อ a > 0 และชนิดคว่ำ เมื่อ a < 0
สรุป ลักษณะของกราฟที่กำหนดด้วยสมการ y = ax2 เมื่อ a ¹ 0
! เมื่อ a > 0 ได้พาราโบลาหงาย จุดต่ำสุดอยู่ที่ (0, 0)
เมื่อ a < 0 ได้พาราโบลาคว่ำ จุดสูงสุดอยู่ที่ (0, 0)
! แกนสมมาตรคือ แกน Y หรือเส้นตรง X = 0 ,
สมการแกนสมมาตรคือ X = 0
! เมื่อ a > 0 ค่าต่ำสุดคือ 0 และ เมื่อ a < 0 ค่าสูงสุดคือ 0
! | a | ยิ่งมากกราฟยิ่งแคบ
2) กราฟที่กำหนดด้วยสมการ y = ax2 + k เมื่อ a ¹ 0 และ k ¹ 0
กราฟที่กำหนดด้วยสมการ y = ax2 + k เมื่อ a ¹ 0 และ k ¹ 0 จะเป็นกราฟพาราโบลาที่มีจุดวกกลับหรือจุดสูงสุดหรือจุดต่ำสุด อยู่ที่ (0, k) และแกนสมมาตรคือ แกน Y
สรุป ลักษณะของกราฟที่กำหนดด้วยสมการ y = ax2 + k
! ถ้า a > 0 ได้พาราโบลาหงาย จุดต่ำสุดอยู่ที่ (0, k) ค่าต่ำสุด = k
ถ้า a < 0 ได้พาราโบลาคว่ำ จุดสูงสุดอยู่ที่ (0, k) ค่าสูงสุด = k
! แกนสมมาตรคือ แกน y หรือเส้นตรง x = 0 สมการแกนสมมาตรคือ x = 0
! ถ้า k > 0 จุดวกกลับอยู่เหนือแกน X
ถ้า k < 0 จุดวกกลับอยู่ใต้แกน X
! ถ้า a, k มีเครื่องหมายเหมือนกัน กราฟไม่ตัดแกน X
ถ้า a, k มีเครื่องหมายต่างกัน กราฟจะตัดแกน X
3. กราฟของ y = a(x – h)2 เมื่อ a ¹ 0 และ h > 0
3.1) กราฟที่กำหนดด้วยสมการ y = a(x – h)2 เมื่อ a ¹ 0 และ h ¹ 0 จะเป็นกราฟ
พาราโบลาที่มีจุดวกกลับหรือจุดสูงสุดหรือจุดต่ำสุดอยู่ที่ (h, 0) และแกนสมมาตรคือเส้นตรง x = h
3.2) กราฟของ y = a(x – h)2 เมื่อ a ¹ 0 และ h < 0
ถ้า h < 0 จะได้สมการใหม่เป็น y = a(x – (-h))2
= a(x + h)2
สรุป ลักษณะของกราฟที่กำหนดด้วยสมการ y = a(x – h)2
! ถ้า a > 0 ได้พาราโบลาหงาย จุดต่ำสุดอยู่ที่ (h, 0) ค่าต่ำสุด = 0
ถ้า a < 0 ได้พาราโบลาคว่ำ จุดสูงสุดอยู่ที่ (h, 0) ค่าสูงสุด = 0
! แกนสมมาตรคือ เส้นตรง x = h สมการแกนสมมาตรคือ x = h
! h > 0 แกนสมมาตรอยู่ทางซ้ายของแกน Y
h < 0 แกนสมมาตรอยู่ทางขวาของแกน Y
4. กราฟของฟังก์ชันกำลังสองที่กำหนดด้วยสมการ y = a(x – h)2 + k เมื่อ a ¹ 0 , h ¹ 0
และ k ¹ 0 จะเป็นพาราโบลาที่มีจุดวกกลับหรือจุดสูงสุดหรือจุดต่ำสุดอยู่ที่ (h, k) และมีแกนสมมาตรคือ เส้นตรง x = h
สรุป ลักษณะของกราฟที่กำหนดด้วยสมการ y = a(x – h)2 + k
! เมื่อ a > 0 ได้พาราโบลาหงาย จุดต่ำสุดอยู่ที่ (h, k) ค่าต่ำสุด = k
เมื่อ a < 0 ได้พาราโบลาคว่ำ จุดสูงสุดอยู่ที่ (h, k) ค่าสูงสุด = k
! ถ้า k > 0 จุดวกกลับอยู่เหนือแกน X
ถ้า k < 0 จุดวกกลับอยู่ใต้แกน X
! แกนสมมาตร คือ เส้นตรง x = h สมการแกนสมมาตรคือ x = h
! ถ้า h > 0 แกนสมมาตรอยู่ทางซ้ายมือของแกน Y
ถ้า h < 0 แกนสมมาตรอยู่ทางขวามือของแกน Y
! ถ้า a และ k มีเครื่องหมายเหมือนกันกราฟไม่ตัดแกน X
ถ้า a และ k มีเครื่องหมายต่างกันกราฟตัดแกน X
5. กราฟที่กำหนดด้วยสมการ y = ax2 + bx + c เมื่อ a ¹ 0 การเขียนกราฟควรจัดสมการให้อยู่ในรูป
y = a(x – h)2 + k จะทำให้เขียนกราฟได้ง่ายขึ้น
จากสมการ y = ax2 + bx + c สามารถเปลี่ยนให้อยู่ในรูป y = a(x – h)2 + k ได้โดยใช้ความรู้เรื่องกำลังสองสมบูรณ์
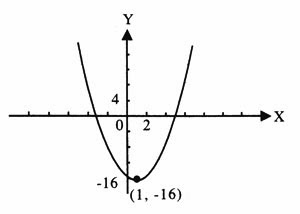
ตัวอย่าง จงหาจุดวกกลับของกราฟของฟังก์ชัน y = 2x2 + 4x – 16
วิธีทำ จาก y = 2x2 + 4x – 16
= 2(x2 + 2x – 8)
= 2{(x2 + 2x + 1) – 8 – 1}
= 2{(x + 1)2 – 9}
= 2(x + 1)2 – 18
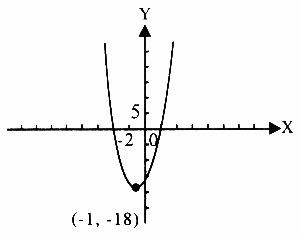
จะได้ h = -1 , k = -18
\ จุดวกกลับคือ (-1, -18)
ฟังก์ชันกำลังสอง
ฟังก์ชันกำลังสอง คือ ฟังก์ชันที่อยู่ในรูป y = ax2 + bx + c เมื่อ a,b,c เป็นจำนวนจริงใดๆ และ a ≠ 0 ลักษณะของกราฟของฟังก์ชันนี้ขึ้นอยู่กับค่าของ a , b และ c และเมื่อค่าของ a เป็นบวกหรือลบ จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ
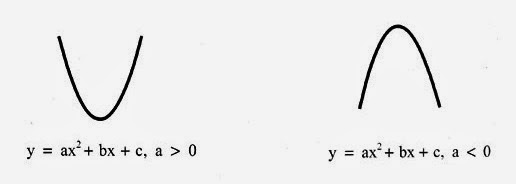
จากรูปจะเห็นว่า ถ้า a > 0 กราฟเป็นเส้นโค้งหงายขึ้น
a < 0 กราฟเป็นเส้นโค้งคว่ำลง
กราฟของฟังก์ชันกำลังสองในรูปนี้มีชื่อว่า พาราโบลา
ในกรณีทั่วไป กราฟของ y = a(x-h)2 + k , a ≠ 0 จะมีจุดที่กราฟวกกลับดังนี้
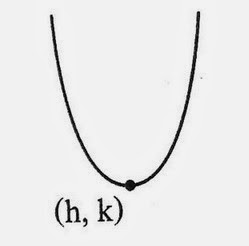
f(x) = a(x-h)2 + k , a > 0
จากรูปกราฟของ f มีจุดวกกลับที่จุด (h,k) ซึ่งเป็นจุดที่ f(x) มีค่าต่ำสุด และ f(h) = k เป็นค่าต่ำสุดของ f
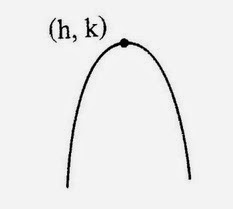
f(x) = a(x-h)2 + k , a < 0
จากรูปกราฟของ f มีจุดวกกลับที่จุด (h,k) ซึ่งเป็นจุดที่ f(x) มีค่าสูงสุด และ f(h) = k เป็นค่าสูงสุดของ f