เนื้อหาคณิต ม.1 เรื่อง ทศนิยมและเศษส่วน และ รูปเรขาคณิตสองมิติและสามมิติ

เนื้อหาคณิต ม.1 เทอม 1 ประกอบด้วย 

• จำนวนเต็ม
• การสร้างทางเรขาคณิต
• เลขยกกำลัง
• ทศนิยมและเศษส่วน
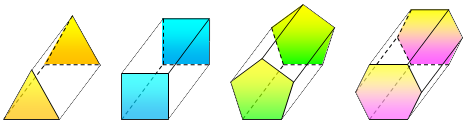
• รูปเรขาคณิตสองมิติและสามมิติ

เนื้อหาคณิต ม.1 เรื่อง ทศนิยมและเศษส่วน และ รูปเรขาคณิตสองมิติและสามมิติ

ทศนิยม(Decimals)
1) ทศนิยมและการเปรียบเทียบทศนิยม
1.1) ความหมายและรูปของทศนิยม
ทศนิยม เป็นสัญลักษณ์ที่ใช้แทนจำ นวนรูปแบบหนึ่ง ซึ่งเกิดจำกกำรหำรจำ นวนที่อยู่ในรูปเศษส่วนโดยนำ
ตัวส่วนไปหำรตัวเศษแล้วได้ผลลัพธ์ที่ไม่ลงตัว หรือเป็นกำรบอกปริมำณของสิ่งต่ำงๆที่ไม่เต็มหน่วย

รูปทศนิยม

จำนวนที่เขียนในรูปทศนิยมจะมี ( . ) เป็นส่วนประกอบตัวเลขที่อยู่หน้ำจุดจะเป็นจำนวนเต็มส่วนตัวเลขที่อยู่หลังจุดเรียกว่าทศนิยม

การอ่านทศนิยม

ทศนิยมประกอบด้วย 2 ส่วน ส่วนที่อยู่หน้ำจุดเป็นจำนวนเต็มอ่านเช่นเดียวกันกับจำนวนเต็มหรือจำนวนนับโดยทั่วไป ส่วนที่อยู่หลังจุดจะอ่านทีละตัวเป็นเลขโดดตามตัวเลขที่มีเช่น 0.35 อ่ำนว่ำ ศูนย์จุดสามห้า

1.2) ค่าประจาหลักและการเขียนในรูปการกระจายการเขียนทศนิยมในรูปการกระจาย เขียนได้ในรูปผลบวกของผลคูณระหว่างเลขในแต่ละหลักกับค่าประจำหลักที่เลขโดดนั้นๆตั้งอยู่ค่าประจาหลักของทศนิยมUntitled

1.3) ค่าสัมบูรณ์ของทศนิยมค่าสัมบูรณ์ของจำนวนใดๆทำได้จากระยะที่จำนวนนั้นๆอยู่ห่างจาก 0 บนเส้นจำนวน

1.4) การเปรียบเทียบทศนิยมเราสามารถเปรียบเทียบทศนิยมสองจำนวนใดๆโดยใช้หลักเกณฑ์ดังต่อไปนี้

1) การเปรียบเทียบทศนิยมที่เป็นบวกสองจำนวนใดๆให้พิจารณาเลขโดดคู่แรกในตำแหน่งเดียวกันที่ไม่เท่ากันจำนวนที่มีเลขโดดในตำแหน่งนั้นมากกว่าจะเป็นจำนวนที่มากกว่า เช่น 2.35 ……. 3.26 3.14 …… 3.32
12.135 ……. 12.134 5.832 ……… 5.831
2) การเปรียบเทียบทศนิยมที่เป็นลบสองจำนวนใดๆ ให้หาค่าสัมบูรณ์ของทั้งสองจำนวน จำนวนที่มีค่าสัมบูรณ์น้อยกว่าจะเป็นจำนวนที่มากกว่า
เช่น -1.83 ……. -2.85 -3.425 ……… -3.321
-5.143 ……… -5.137 -0.157 ………. -0.125
3) การเปรียบเทียบทศนิยมที่เป็นบวกและทศนิยมที่เป็นลบ เนื่องจากทศนิยมที่เป็นบวกอยู่ทางขวาของ 0 ดังนั้นทศนิยมที่เป็นบวกจะมากกว่าทศนิยมที่เป็นลบเสมอ

2 ) การบวกและการลบทศนิยม
เราสามารถสรุปหลักเกณฑ์การบวกทศนิยมได้ดังนี้
1. การหาผลบวกระหว่างทศนิยมที่เป็นบวก ให้นำค่าสัมบูรณ์มาบวกกันแล้วตอบเป็นจำนวนบวก
2. การหาผลบวกระหว่างทศนิยมที่เป็นลบ ให้นำค่าสัมบูรณ์มาบวกกันแล้วตอบเป็นจำนวนลบ
3. การหาผลบวกระหว่างทศนิยมที่เป็นบวกกับทศนิยมที่เป็นลบ ให้นำค่าสัมบูรณ์มาลบกันแล้วตอบเป็นจำนวนบวกหรือลบตามจำนวนที่มีค่าสัมบูรณ์มากกว่า
นอกจากนี้ เรายังสามารถใช้หลักเกณฑ์เดียวกันนี้ในการหาผลลบของทศนิยม โดยการเปลี่ยนรูปการลบให้อยู่ในรูปการบวกดังนี้
ตัวตั้ง – ตัวลบ = ตัวตั้ง + จำนวนตรงข้ำมของตัวลบ
เช่น 2.13 – 1.12 = 2.13 + (-1.12 )

3) การคูณและการหารทศนิยม

การคูณทศนิยม มีหลักการเช่นเดียวกับการคูณจำนวนเต็มโดยกำรเปลี่ยนทศนิยมทั้งตัวตั้งและตัวคูณให้เป็นจำนวนเต็มแต่จำนวนตำแหน่งของทศนิยมของผลลัพธ์จะเท่ากับผลบวกของจำนวนตำแหน่งของทศนิยมตัวตั้งและตัวคูณ

การหารทศนิยม มีหลักการดังนี้
1. ต้องทำ ตัวหารให้เป็นจำนวนเต็มโดยการนำ 10 , 100 , 1000 , . . . มาคูณทั้งตัวตั้งและตัวหาร
2. ถ้าตัวตั้งและตัวหารเป็นทศนิยมที่เป็นบวกให้นำค่าสัมบูรณ์มาหารกันแล้วตอบเป็นจำนวนบวก
3. ถ้าตัวตั้งและตัวหารเป็นทศนิยมที่เป็นลบให้นำค่าสัมบูรณ์มาหารกันแล้วตอบเป็นจำนวนบวก
4. ถ้าตัวตั้งเป็นจำนวนบวกและตัวหารเป็นจำนวนลบหรือตัวตั้งเป็นจำนวนลบและตัวหารเป็นจำนวนบวก
ให้นำค่าสัมบูรณ์ของตัวตั้งและตัวหารมาหารกันแล้วตอบเป็นจำนวนลบ

เศษส่วน (Fraction)
เศษส่วน หมายถึง จำนวนที่ใช้บอกปริมาณที่ไม่เป็นจำนวนเต็มซึ่งจะเขียนในรูป a b เมื่อ a และ b เป็นจำ นวนเต็ม โดยที่ b # 0
ชนิดของเศษส่วน แบ่งออกเป็นดังนี้
1) เศษส่วนแท้ หรือเศษส่วนสามัญ หมายถึงเศษส่วนที่มีตัวเศษน้อยกว่าตัวส่วน
2) เศษส่วนเกิน หมำยถึง เศษส่วนที่มีตัวเศษมากกว่าตัวส่วน
3) เศษส่วนจานวนคละ หมำยถึง เศษส่วนที่มีจำ นวนเต็มและเศษส่วนแท้รวมอยู่ด้วยกันข้อสังเกตเกี่ยวกับเศษส่วนจานวนคละ

3.1) เศษส่วนจำนวนคละสามารถเขียนในรูปผลบวกได้

3.2) เศษส่วนจำนวนคละสามารถเขียนในรูปเศษส่วนเกินได

การคูณและการหารเศษส่วน
การคูณเศษส่วน เป็นเศษส่วนที่ b และ d ไม่เท่ำกับศูนย์ ผลคูณของ a

หลักเกณฑ์กำรคูณจำ นวนเต็มและข้อตกลง
การหารเศษส่วน มีหลักกำรดังนี้
1) ถ้ำเป็นเศษส่วนจำ นวนคละให้เปลี่ยนเป็นเศษส่วนเกิน
2) เปลี่ยนเครื่องหมำยหำรเป็นเครื่องหมำยคูณ แล้วเปลี่ยนตัวหำรโดยกลับเศษเป็นส่วน กลับส่วนเป็นเศษ

เรขาคณิตสองมิติและสามมิติ

สูตรคำนวณเรขาคณิตสองมิติ
สูตรรูปสามเหลี่ยม
สูตรรูปสี่เหลี่ยม
สูตรรูปหลายเหลี่ยม
เรขาคณิตสามมิติ
สูตรคำนวณเรขาคณิตสามมิติ
สูตรรูปทรงปริซึม
สูตรลูกบาศก์
สูตรรูปทรงกระบอกตัน
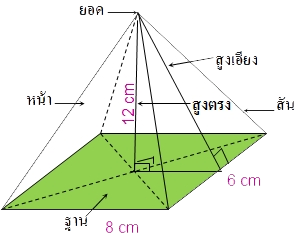
สูตรรูปทรงพีระมิด
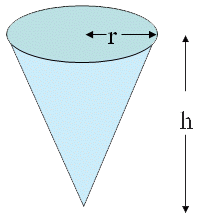
สูตรรูปทรงกรวย
สูตรรูปทรงกลม
สูตรรูปทรงกระบอกที่มีหน้าตัดรูปวงแหวน (รูปทรงกระบอกกรวย)