คณิตศาสตร์ ม. 3 เรื่อง พื้นที่ผิวและปริมาตร
– ภาคตัดกรวย
– ปริมาตรทรงกรวย (animation)
ภาคตัดกรวย
ในทางคณิตศาสตร์ หมายถึง เส้นโค้งที่ได้จากการตัดพื้นผิวกรวยกลม ด้วยระนาบแบน ภาคตัดกรวยนี้ถูกตั้งเป็นหัวข้อศึกษาตั้งแต่สมัย 200 ปีก่อนคริสต์ศักราชโดย อพอลโลเนียส แห่ง เพอร์กา ผู้ซึ่งศึกษาภาคตัดกรวยและค้นพบสมบัติหลายประการของภาคตัดกรวย ต่อมากรณีการศึกษาภาคตัดกรวยถูกนำไปใช้ประโยชน์หลายแบบ ได้แก่ ในปี พ.ศ. 2133 (ค.ศ. 1590) กาลิเลโอ กาลิเลอี พบว่าขีปนาวุธที่ยิงขึ้นไปในมุมที่กำหนดมีวิถีการเคลื่อนที่โค้งแบบพาราโบลา, ใน พ.ศ. 2152 (ค.ศ. 1609) โยฮันส์ เคปเลอร์ พบว่าวงโคจรของดาวเคราะห์รอบนอกเป็นรูปวงรี เป็นต้น ในกรณี ดีเจนเนอเรต ระนาบจะตัดผ่านจุดยอดของกรวย และได้ผลของการตัดเป็น จุด เส้นตรง หรือ เส้นตรงสองเส้นตัดกัน กรณีเหล่านี้ไม่ได้ถูกรวมไว้ในภาคตัดกรวย ในเรขาคณิตเชิงภาพฉาย (projective geometry) นั้น ภาพฉายบนระนาบ ของภาคตัดกรวยแต่ละชนิดนั้นจะเหมือนกัน ขึ้นอยู่กับลักษณะการฉาย หรือที่เรียกว่า การแปลงเชิงภาพฉาย (projective transformation)
ชนิดภาคตัดกรวย (Conic Section)
วงกลม และ วงรี คือ เส้นโค้งซึ่งได้จากการตัดกรวย ด้วยระนาบ ให้ได้เส้นโค้งปิด (เป็นวง) วงกลมนั้นถือเป็นกรณีพิเศษของวงรี โดยแนวของระนาบในการตัดนั้น ตั้งฉากกับแกนกลางของกรวย หากระนาบตัดกรวยในแนวขนานกับเส้นขอบของกรวย หรือเรียก เส้นกำเนิดกรวย (generator line) จะได้เส้นโค้งเรียกว่า พาราโบลา หากระนาบไม่อยู่ในแนวขนานเส้นขอบ และตัดกรวยได้เส้นโค้งเปิดไม่เป็นวง จะเรียกเส้นโค้งนี้ว่า ไฮเพอร์โบลา จะเห็นได้ว่าในกรณีนี้ระนาบจะตัดกรวยทั้งครึ่งบน และครึ่งล่าง ได้เป็นเส้นโค้งที่ขาดจากกันสองเส้น
ในกรณีที่เรียกว่าในภาษาอังกฤษว่า ดีเจนเนอเรต ระนาบจะตัดผ่านจุดยอดของกรวย และได้ผลของการตัดเป็น จุด เส้นตรง หรือ เส้นตรงสองเส้นตัดกัน กรณีเหล่านี้ไม่ได้ถูกรวมไว้ในภาคตัดกรวย
เส้นโค้งที่เกิดจาการตัดกรวย ประกอบด้วย
- วงกลม (Circle)
- วงรี (Ellipse)
- พาราโบลา (Parabola)
- ไฮเพอร์โบลา (Hyperbola)1. หากระนาบขนานไปกับฐานกรวย ขอบหน้าตัดจะเป็นรูปวงกลม
2. หากระนาบเอียง แต่ยังไม่เอียงจนตัดไปถึงฐานกรวย ขอบหน้าตัดจะเป็นรูปวงรี
3.หากระนาบเอียงจนตัดฐานกรวยหนึ่ง ขอบหน้าตัดจะเป็นโค้งที่มีชื่อว่า พาราโบลา
4.หากระนาบเอียงจนไปตัดกรวยอีกฟาก ขอบหน้าตัดจะเกิดเป็นโค้งที่มีชื่อว่า ไฮเปอร์โบลา
กราฟและสมการของภาคตัดกรวยแต่ละชนิด โดยอาศัยหลักการเลื่อนกราฟ ได้ดังตารางต่อไปนี้
| ภาคตัดกรวย | กราฟ | สมการรูปแบบมาตรฐานและข้อเท็จจริงที่สำคัญ |
| วงกลม | 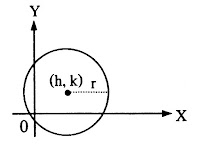 |
สมการ
จุดศูนย์กลาง (h, k) รัศมียาว r หน่วย |
| วงรี | 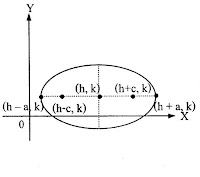 |
สมการ
แกนเอกอยู่ในแนวนอน จุดศูนย์กลาง (h, k) จุดยอด (h-a, k), (h+a, k) โฟกัส (h-c, k), (h+c, k); c2= a2 – b2 แกนเอกยาว 2a หน่วย แกนโทยาว 2b หน่วย |
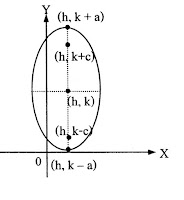 |
สมการ
แกนเอกอยู่ในแนวตั้ง จุดศูนย์กลาง (h, k) จุดยอด (h, k-a), (h, k+a) โฟกัส (h, k-c), (h, k+c); c2= a2 – b2 แกนเอกยาว 2a หน่วย แกนโทยาว 2b หน่วย |
|
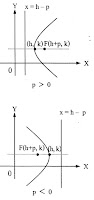
| พาราโบลา | 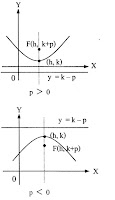 |
สมการ
แกนสมมาตรอยู่ในแนวตั้ง จุดยอด (h, k) โฟกัส (h, k+p) P > 0 เส้นโค้งหงายขึ้น P < 0 เส้นโค้งคว่ำลง ไดเรกตริกซ์ y = k – p |
 |
สมการ
แกนสมมาตรอยู่ในแนวตั้ง จุดยอด (h, k) โฟกัส (h+p, k) P > 0 เส้นโค้งเปิดด้านขวา P < 0 เส้นโค้งเปิดด้านซ้าย ไดเรกตริกซ์ x = h – p |
|
| ไฮเพอร์โบลา | 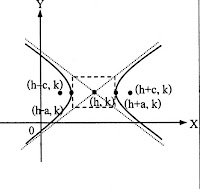 |
สมการ
แกนตามขวางอยู่ในแนวนอน จุดศูนย์กลาง (h, k) จุดยอด (h-a, k), (h+a, k) โฟกัส (h-c, k), (h+c, k); c2= a2 + b2 แกนตามขวางยาว 2a หน่วย แกนสังยุคยาว 2b หน่วย |
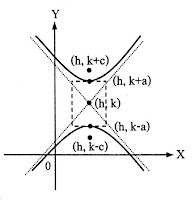 |
สมการ
แกนเอกอยู่ในแนวตั้ง จุดศูนย์กลาง (h, k) จุดยอด (h, k-a), (h, k+a) โฟกัส (h, k-c), (h, k+c); c2= a2 + b2 แกนตามขวางยาว 2a หน่วย แกนสังยุคยาว 2b หน่วย |
สมการทั่วไปของภาคตัดกรวย
กราฟของสมการ เมื่อ A และ C ไม่เป็นศูนย์พร้อมกันเป็นภาคตัดกรวยหรือภาคตัดกรวยลดรูป ในกรณีที่ไม่ใช่ภาคตัดกรวยลดรูป กราฟของสมการเป็น
- วงกลม ถ้า A = C
- วงรี ถ้า AC > 0
- พาราโบลา ถ้า AC = 0
- ไฮเพอร์โบลา ถ้า AC < 0
ปริมาตรทรงกรวย
กรวย คือ รูปเรขาคณิตสามมิติ มีฐานเป็นวงกลม มียอดแหลมที่ไม่อยู่บนระนาบเดียวกันกับฐานและเส้นที่ต่อระหว่างจุดยอดและจุดใดๆ บนขอบของฐานเป็นส่วนของเส้นตรง
รูปเรขาคณิตสามมิติ
รูปเรขาคณิตสามมิติ
ระดับชั้นมัธยมต้นนี้ นักเรียนควรมีพื้นฐานเกี่ยวกับ พื้นที่ผิวและปริมาตรที่ควรทราบ ดังนี้
ปริซึม
ปริซึม เป็นรูปเรขาคณิตสามมิติที่มีหน้าตัด(ฐาน) ทั้งสองข้างเป็นรูปหลายเหลี่ยมที่เท่ากันทุกประการหน้าตัด (ฐาน) ทั้งสองอยู่ในระนาบที่ขนานกัน มีหน้าข้างเป็นรูปสี่เหลี่ยมมุมฉาก การเรียกชื่อปริซึมจะเรียกตามรูปหน้าตัดของปริซึมส่วนต่างๆของปริซึมมีชื่อเรียก
ดังนี้
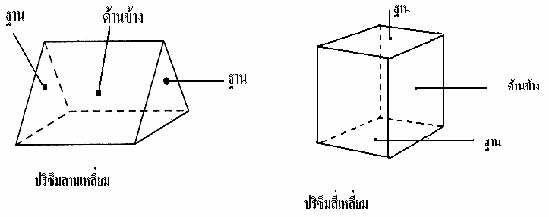
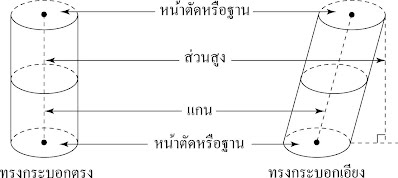
ทรงกระบอก เป็นรูปเรขาคณิตสามมิติที่มีฐานสองฐานเป็นรูปวงกลมที่เท่ากันทุกประการและอยู่บนระนาบที่ขนานกัน และเมื่อตัดรูปเรขาคณิตสามมิตินั้นด้วยระนาบที่ขนานกับฐานแล้ว จะได้หน้าตัดเป็นวงกลมที่เท่ากันทุกประการกันฐานเสมอ ด้านข้างเป็นผิวเรียบโค้งส่วนต่างๆของทรงกระบอก
ข้อแตกต่างของปริซึมกับทรงกระบอก คือ
– ฐาน ปริซึมเป็นรูปหลายเหลี่ยมทรงกระบอกเป็นวงกลม- ด้านข้าง ปริซึมเป็นรูปสี่เหลี่ยมผืนผ้าทรงกระบอกเป็นผิวเรียบโค้ง
พีระมิด
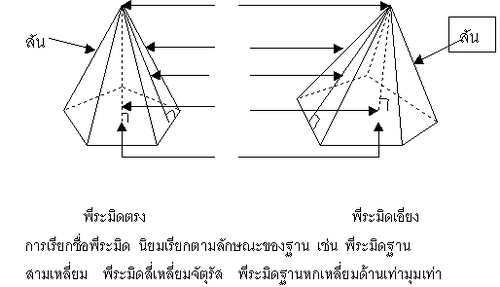
พีระมิด เป็นรูปเรขาคณิตสามมิติที่มีฐานเป็นรูปเหลี่ยมใดๆ มียอดแหลมที่ไม่อยุ่บนระนาบเดียวกันกับฐาน และหน้าทุกหน้าเป็นรูปสามเหลี่ยมที่มีจุดยอดร่วมกันที่ยอดแหลมนั้น การเรียกชื่อพีระมิดจะเรียกตามรูปฐานของพีระมิด ส่วนต่างๆของพีระมิด
กรวย
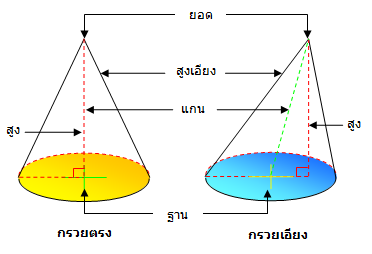
กรวย เป็นรูปเรขาคณิตสามมิติที่มีฐานเป็นรูปวงกลม มียอดแหลมที่ไม่อยู่ในระนาบเดียวกันกับฐาน และเส้นที่ต่อระหว่างจุดยอดกับจุดใดๆ บนขอบของฐานเป็นส่วนของเส้นตรงดด้านข้างเป็นผิวโค้งเรียบระมิ ส่วนต่างๆของกรวย
ข้อแตกต่างของพีระมิดกับกรวย คือ- ฐาน พีระมิดฐานรูปหลายเหลี่ยมกรวยฐานรูปวงกลม
– ด้านข้าง พีระมิดเป็นรูปสามเหลี่ยมผืนผ้ากรวยเป็นผิวเรียบโค้ง
ทรงกลม
ทรงกลม เป็น รูปเรขาคณิตสามมิติที่มีด้านข้างเป็นผิวโค้งเรียบ และจุดทุกจุดบนผิวโค้งอยู่ห่างจากจุดคงที่จุดหนึ่งเป็นระยะเท่ากัน เรียกจุดคงที่ว่า จุดศูนย์กลางของทรงกลมเรียกระยะที่เท่ากันว่า รัศมีของทรงกลม ส่วนต่างๆของทรงกลม






