สรุปสูตรกฎของลอการิทึม ( Logarithm function )

เรื่อง ฟังก์ชัน ลอการิทึม ( Logarithm function ) เป็นเนื้อหาในวิชาคณิตศาสตร์ เพิ่มเติม ระดับม.5

กฎของลอการิทึม

นิยาม ถ้า a>0, a≠1และ m,n เป็นจำนวนเต็มบวก
1. log_a MN= log_a M+ log_a N
2. log_a = log_a M- log_a N
3. log_a m^p = P log_a M
4. a ^log_a^M = M
5. log_a M =
6. log_a a = 1
7. log_a 1= 0. 8. Log_b a =

สมบัติที่สำคัญของลอการิทึมมีดังต่อไปนี้

logaMN=logaM+logaN ลอกคูณเท่ากับลอกบวก
logaMN=logaM−logaN ลอกหารเท่ากับลอกลบ
logaMk=klogaM.
logaa=1.
loga1=0.
logakM=1klogaM.
logba=1logab.
logba=logalogb ข้อนี้เป็นการเปลี่ยนฐานล็อก

ฟังก์ชันเอ็กโปเนนเชียลและลอการิทึม
กฎของเลขยกกำลัง
ถ้า a,b เป็นจำนวนจริงใดๆจะได้
1. a^m+ aⁿ = a^m+n
2. (ab)ⁿ = aⁿbⁿ
3. (a^m)ⁿ = a^mn
f = { (x,y) | R x R⁺ | y = a^x ; a > 0 และ a น 1 } เรียกว่า ฟังก์ชันเอกซ์โปเนนเชียล จาก y = a^x , a > 0, a น 1 จะได้ x ฮ R และ y ฮ R⁺ นั่นคือ โดเมนเป็นเซตของจำนวนจริง และเรนจ์เป็นเซตของจำนวนจริงบวก

1. ถ้า a > 1 ฟังก์ชันเอกโพเนนเชียลเป็นฟังก์ชันเพิ่ม
2. ถ้า 0 < a < 1 ฟังก์ชันเอกโพเนนเชียลเป็นฟังก์ชันลด
3. สมบัติที่สำคัญคือ e^x = e^y ก็ต่อเมื่อ x = y ส่วนสมบัติอื่นๆมีเช่นเดียวกับเลขยกกำลัง

การแก้สมการเอ็กโปเนนเชียล
การแก้สมการเอกโพเนนเชียลที่มักพบอยู่บ่อยๆมี 4 วิธี คือ
1. ทำให้ฐานเท่ากัน คือทำให้ a^p(x) = a^q(x) แล้วสรุปว่า p(x) = q(x)
2. ทำให้กำลังเหมือนกันแต่ฐานต่างกัน คือ a^p(x) = b^q(x) แล้วสรุปได้ว่า p(x) = 0
3.ทำให้เป็นเลขจำนวนเดียวยกกำลังแล้วมีค่าเท่ากับ 1 คือทำเป็น (abc)^u = 1 แล้วสรุปว่า u = 0

การแก้อสมการเอกซ์โพเนนเชียล

กลุ่มที่ 1 ฐานเหมือนกันเลขชี้กำลังต่างกัน

1. เมื่อ	a > 1	จะได้ว่า อสมการของเลขชี้กำลังจะคล้อยตามอสมการของเลขยกกำลัง
เช่น	a^x > a^y	จะได้ว่า x > y
	a^x < a^y	จะได้ว่า x < y
2. เมื่อ	0 < a < 1	จะได้ว่า อสมการของเลขชี้กำลังจะตรงข้ามกับอสมการของเลขชี้กำลัง
เช่น	a^x > a^y	จะได้ว่า x < y
	a^x < a^y	จะได้ว่า x > y

กลุ่มที่ 2 ฐานต่างกันเลขชี้กำลังเหมือนกัน

1.	ถ้าอสมการของเลขยกกำลังคล้อยตามอสมการของเลขฐานจะได้ว่าเลขชี้กำลัง < 0
	เช่น a < b , a^x < b^x จะได้ว่า x > 0
	a > b , a^x > b^x จะได้ว่า x > 0
2.	ถ้าอสมการของเลขยกกำลังตรงข้ามกับอสมการของเลขฐานจะได้ว่าเลขชี้กำลัง < 0
	เช่น a > b , a^x < b^x จะได้ว่า x < 0
	a < b , a^x > b^x จะได้ว่า x < 0
	y = log_a x มีความหมายว่า x = a^y
	ถ้า a = 10 เรียกว่า ลอการิทึมสามัญ เขียนแทนด้วย log x ถ้า a = e ป 2.71828 เรียกว่า ลอการิทึมธรรมชาติ เขียนแทนด้วยสัญลักษณ์ ln x ( คือ log_e x ) โดเมนของฟังก์ชันลอการิทึมเป็นเซตของจำนวนจริงบวก เรนจ์ของฟังก์ชันลอการิทึมเป็นเซตของจำนวนจริง

สมบัติที่สำคัญ
1. 2.	log_a x log_a xy	= =	log_a y ก็ต่อเมื่อ x = y log_a x + log_a y
3. 4.	log_a(x/y) log_a x^y	= =	log_a x + log_a y ylog_a x + log_a
5.	log_aa	=	1
6.	log_a1	=	0
7.	ln 1	=	log 1 = 0
8.	ln e	=	1, log 10 =1
9.	e^{ln x}	=	x , 10^{log x} = x
10.	ln e^x	=	x , log 10^x = x
13.	a^x	=	e^{x ln a}

การหาค่า log x เขียน x = A ด 10ⁿ เมื่อ 1 < A < 10 หาค่าของ log A จากตาราง แล้วจะได้
log x = n + log A

ตัวอย่าง log 5710

= log (5.71 ด 103)
= 3 + log 5.71
= 3 + 0.7566 = 3.7566

การหาค่า x เมื่อทราบค่า log x เช่น log x = 7.8341 ค่า x ทำได้โดยการใช้เครื่องคิดเลขและการเปิดตาราง
1. เขียน log x = n + B เมื่อ 0 < B < 1 และ n เป็นจำนวนเต็ม
2. หาค่า y เมื่อ log y = B จากตารางแอนติลอการิทึมหรือตารางลอการิทึม (โดยดูย้อนกลับ) ได้ค่า y
แล้วจะได้ x = y ด 10ⁿ

การแก้สมการลอการิทึม การแก้สมการลอการิทึมมีรูปแบบที่พบกันบ่อยๆอยู่ 4 วิธี คือ
1. แยกตัวประกอบ เช่น (log 4 x)³-(log 4 x)² – 2log 4 x = log 4 x (log 4 x – 2)( log 4 x + 1 ) = 0
2. เปลี่ยนรูป y = log_ax เป็น x = a^y
3. ทำให้เป็นลอการิทึมฐานเดียวกันมีค่าเท่ากันคือทำให้ log _a u = log _a v แล้วสรุปว่า u = v
4. แปลงรูปสมการโดยใช้สมบัติของลอการิทึม

การแก้อสมการลอการิทึม อสมการลอการิทึมสามารถแก้ได้โดยใช้สมบัติต่อไปนี้คือ
1. กรณีที่ a > 0 จะได้ว่า log_au > log_a v ก็ต่อเมื่อ u > v
2. กรณีที่ 0 < a < 1 จะได้ว่า log_a u > log_a v ก็ต่อเมื่อ u < v
3. แปลงอสมการลอการิทึมให้อยู่ในรูปอสมการเอกซ์โพเนนเชียล เช่น
log₃( x + 2 ) < 4 = x + 2 < 3⁴

ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม

จากเรื่องฟังก์ชันเอกซ์โปเนนเชียล ถ้าให้ƒ แทนฟังก์ชันเอกซ์โปเนนเชียล ƒ จะมีลักษณะดังนี้

1. ƒ : R→R⁺

2. ƒ = {(x,y) : y = a^x , a > 0 , a≠1 }

เนื่องจากว่าฟังก์ชันเอกซ์โปเนนเชียลเป็นฟังก์ชันแบบหนึ่งต่อหนึ่ง (ค่า x หนึ่งค่า ให้ค่า y หนึ่งค่า)

ดังนั้น อินเวอร์สของฟังก์ชันเอกซ์โปเนนเชียลจึงเป็นฟังก์ชันหนึ่งต่อหนึ่งด้วย

ดังนี้

1. ƒ^-1 : R⁺→R

2. ƒ^-1 = {(x,y) : x = a^y , a > 0 , a≠1 }

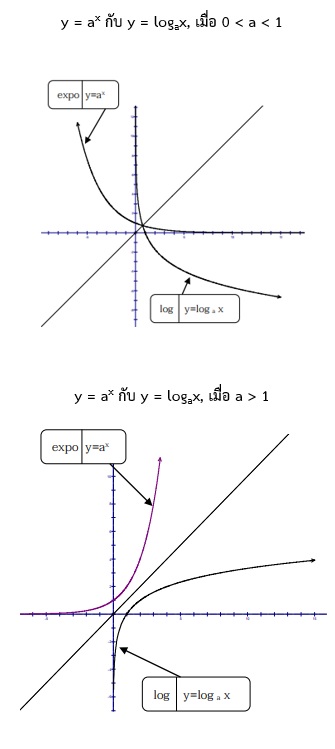
จาก x = a^yสามารถเขียนได้ในรูปของ y =ƒ^-1(x) โดยเราจะกำหนดสัญลักษณ์ได้เป็นy = log_ax (อ่านว่าลอการิทึมเอกซ์ฐานเอ หรือ ล็อกเอกซ์ฐานเอ)ดังนั้นฟังก์ชันอินเวอร์สของฟังก์ชันเอกซ์โปเนนเชียลจึงเขียนได้เป็น ƒ^-1 = {(x,y) : x = a^y , a > 0 , a≠1 }

ข้อสังเกตของกราฟในกรณี y = log_ax ; a > 0, a ≠1

1. กราฟของฟังก์ชันลอการิทึม จะตัดแกน y ที่คู่อันดับ(1, 0)

2. โดเมนของฟังก์ชันลอการิทึม คือเซตของจำนวนจริงบวก เรนจ์ของฟังก์ชันลอการิทึม คือเซตของจำนวนจริง

3. กรณีที่ a อยู่ในช่วง (1, ∞) แล้ว y = log_ax จะเป็นฟังก์ชันลด

กรณีที่ a อยู่ในช่วง(0, 1) แล้ว y = log_ax จะเป็นฟังก์ชันเพิ่ม

4.ฟังก์ชันลอการิทึม เป็นฟังก์ชัน 1-1 จาก R⁺ไปทั่วถึง R

นั่นคือ log_ax = log_ay ก็ต่อเมื่อ x = y

5. การเปรียบเทียบฟังก์ชันลอการิทึม

กรณี a อยู่ในช่วง(0, 1) เป็นฟังก์ชันลด จะได้ว่า

x > y ก็ต่อเมื่อ log_ax < log_ay

x < y ก็ต่อเมื่อ log_ax > log_ay

กรณี a อยู่ในช่วง(1,∞) เป็นฟังก์ชันเพิ่ม จะได้ว่า

x > y ก็ต่อเมื่อ log_ax > log_ay

x < y ก็ต่อเมื่อ log_ax < log_ay

การหาค่าลอการิทึมสามัญโดยใช้ตาราง

เนื่องจากในตารางระบุเพียงค่า
log 1 จนถึง log
9.99 เท่านั้น
หากต้องการหาค่า log N เราจะต้องเขียนจำนวน N เป็นรูป N₀×10ⁿเมื่อ 1≤ N₀ < 10 และใช้กฎของลอการิทึมว่า log N = log(N₀×10ⁿ) = log N₀ + n