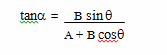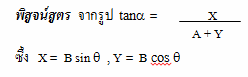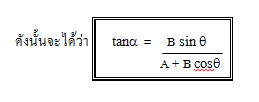ใช้กฎของ cosθ หรือ กฎของโคไซน์
กฎของไซน์ (The Law of Sines)
เดินทางมาถึงเรื่องสุดท้ายท้ายสุดในตรีโกณมิติ ม.5 ซึ่ง เป็นเรื่องที่สูตรไม่เยอะ และค่อนข้างง่าย ดังนั้นไปเริ่มกันเลยครับ
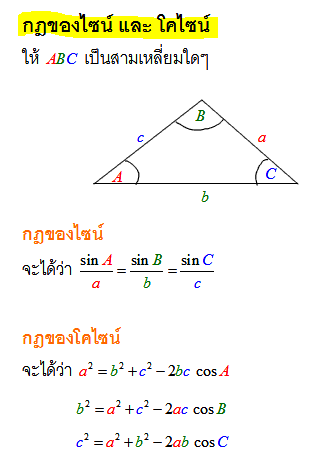
กฎของไซน์กับกฎของโคไซน์นั้นให้น้องจำไว้เลยว่า เกี่ยวกับสามเหลี่ยม ซึ่งใน ม.3 เราเรียนเรื่องสามเหลี่ยมมุมฉาก กันไปแล้วในตรีโกณมิติ ม.3 พอมา ม.5
จากกฎของ cos สามารถหาขนาดหรือความยาวของ R ได้เท่านั้น
ถ้านำแรง 2 แรงมาเขียนรูปตามทฤษฎีสี่เหลี่ยมด้านขนานจะได้ดังรูป
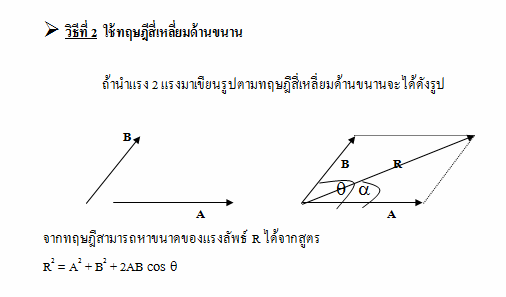
การใช้กฎของ cos เราใช้ด้านตรงข้ามมุม และใช้สูตรเป็น –
ซึ่งจะใช้สูตร R2 = A2 + B2 – 2AB cos q ( q คือมุมภายในสามเหลี่ยมและอยู่ตรงข้ามกับ R)
พิสูจน์สูตร จากรูป X = B sin q
Y = B cos q
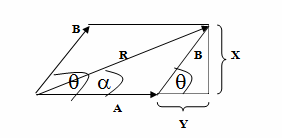
ตามรูป และ Pythagorus ( รูปสามเหลี่ยมมุมฉาก , รูปใหญ่ )
R2 = (A + Y)2 + X2
= (A + B cos q)2 + (B sin q)2
= A2 + 2AB cos q + B2 cos2 q + B2 sin2 q
= A2 + 2AB cos q + B2 ( sin2 q + cos2 q )
จากตรีโกณ sin2 q + cos2 q = 1 ดังนั้นจะได้ว่า
และหาทิศของ R หรือมุม a ได้จากสูตร