คณิตศาสตร์เรื่อง-ความสัมพันธ์(Relation)

บทนิยาม    r  เป็นความสัมพันธ์จาก   A  ไป  B  ก็ต่อเมื่อ r เป็นสับเซตของ  A x B

นั่นคือ  ความสัมพันธ์เป็นเซตของคู่อันดับ

ตัวอย่างที่ 4   กำหนดให้   A  = {1,2,3,4}  ,  B  =  {0,2,4,6}

ให้   r₁  แทนความสัมพันธ์  “ น้อยกว่า”  จาก A ไป B      จะได้

r₁   =  {(a,b)∊  AxB | a < b} ……[แบบเงื่อนไข]

และ         r₁  =  {(1,2),(1,4),(1,6),(2,4),(2,6),(3,4),(3,6),(4,6)}  ……… [แบบแจกแจง]

ให้  r₂   แทนความสัมพันธ์  “ หารลงตัว “  จาก B  ไป  A   จะได้

r₂  =  {(b,a) ∊ B x A | b|a }

r₂  =  {(2,2),(2,4),(4,4)}

 ตัวอย่างที่ 5    กำหนด   A  =  {x | x เป็นจำนวนเต็ม}

ฺฺB   =  {x |x เป็นจำนวนเต็มบวก}

     ถ้า         r₁  =   {(x,y) ∊ A x B | y = x² }  เขียน  r₁ แบบแจกแจงสมาชิกได้ดังนี้

r₁  =  {(1,1),(-1,1),(2,4),(-2,4),… }

ถ้า           r₂  =  {(x,y) ∊ A x B | y =  }  เขียน  r _2­ แบบแจกแจงสมาชิกได้ดังนี้

r_2­   =   {(2,1),(4,2),(6,3),(8,4) ,…}

คู่อันดับ
คู่อันดับประกอบด้วยสมาชิกสองตัว เขียนแทนคู่อันดับในรูป (a,b) โดยที่ a เป็นสมาชิกตัว
หน้า และ b เป็นสมาชิกตัวหลัง
การสลับที่กันของคู่อันดับระหว่างสมาชิกตัวหน้ากับสมาชิกตัวหลัง (a,b) (b,a) จะท าให้
ความหมายของคู่อันดับเกิดการเปลี่ยนทันที ดังนั้น จึงสามารถสรุปหลักการของคู่อันดับได้ ดังนี้
1. ถ้า (a,b) = (b,a) ก็ต่อเมื่อ a=b
2. ถ้า (a,b) = (c,d) ก็ต่อเมื่อ a=c และ b=d
3. ถ้า (a,b) (c,d) ก็ต่อเมื่อ a c หรือ b d
ผลค ูณคาร์ทีเชียน
ผลคูณคาร์ทีเชียนของเซต A และ B คือ เซตของคู่อันดับ (a,b) ที่มีสมาชิกตัวหน้าเป็น
เซตของ A และสมาชิกตัวหลังเป็นเซตของ B กล่าวคือ
AxB = {(a,b) | a∊A, b∊B}

ความสัมพันธ์ (Relations) ใน นิยาม 1 ให้ A และ B เป็นเซต จะเรียก r ว่าเป็นความสัมพันธ์จาก A ไป B ถ้า r เป็นเซตย่อยของA  X B

ความสัมพันธ์ทวิภาค(Binary Relation ) จาก A ไป B คือ เซตของคู่ลำดับโดยที่สมาชิกคู่อันดับตัวแรกมาจาก A และคู่ลำดับที่สองมาจาก B
เราใช้สัญลักษณ์ a R b แทน (a,b) ฮ R และ a ~R b แทน (a,b) ฯ R
นอกจากนั้นเมื่อ (a,b) เป็นสมาชิกใน R จะบอกว่า a สัมพันธ์กับ b โดย R

ความสัมพันธ์ทวิภาค(Binary Relation) เป็นการแสดงความสัมพันธ์ระหว่างสมาชิกของ 2 เซต
สำหรับความสัมพันธ์ระหว่าง สมาชิกในเซตที่มากกว่า 2 เซตขึ้นไปจะกล่าวทีหลัง

ในบทนี้เราจะใช้คำว่า ความสัมพันธ์ แทน ความสัมพันธ์ทวิภาค

ตัวอย่างของความสัมพันธ์ดังนี้

ตัวอย่างที่ 1 ให้ A เป็นเซตของนักเรียนในโรงเรียน และ B เป็นเซตของวิชา
ให้ R เป็นความสัมพันธ์ที่ประกอบด้วยคู่ลำดับ (a,b) โดยที่ a เป็นนักเรียนที่ลงทะเบียนเรียนในวิชา b
ตัวอย่างเช่น ถ้าJason Goodfriend และ Deborah Sherman ลงทะเบียนเรียนใน CS518 นั่นคือ วิชา Discrete Mathematics คู่ลำดับที่ได้ (Jason Goodfriend, CS518) และ
(Deborah Sherman, CS518) เป็นสมาชิกของความสัมพันธ์ R ถ้า Jason Goodfriend ลงทะเบียนเรียนใน CS510 นั่นคือ วิชา Data Structure แล้ว คู่ลำดับ (Jason Goodfriend, CS510) และยังเป็นความสัมพันธ์บน R
อย่างไรตาม ถ้า Deborah Sherman ไม่ได้ลงทะเบียนเรียนใน CS510 แล้วคู่ลำดับ(Deborah Sherman, CS510) ไม่อยู่บนความสัมพันธ์ R

ตัวอย่างที่ 2 ให้ A เป็นเซตของ ประชากรทั้งหมด และ B เป็นเซตของรัฐ 50 รัฐในประเทศอเมริกา กำหนดให้ความสัมพันธ์ R โดยมีรายละเอียดดังนี้ คู่ลำดับ (a,b) เป็นสมาชิกของความสัมพันธ์ R ถ้าเมือง a อยู่ใน รัฐ b
ตัวอย่างเช่น (Boulder,Colorado),(Bangor,Maine),(Ann Arbor,Michigan),(Cupertino,California) และ (Red Bank,New Jersey) อยู่บนความสัมพันธ์ R

ตัวอย่างที่ 3 ให้ A = {0,1,2,} และ B = { a,b} แล้ว{ (0,a) , (0,b) , (1,a) , (2,b) } เป็นความสัมพันธ์จาก A ไป B

และได้ว่า 0 R a แต่ 1 ~R b
ความสัมพันธ์สามารถเขียนแทนด้วยกราฟได้ดังรูปที่ 1 (a)
หรือแทนด้วยตาราง ดังรูปที่ 1 (b)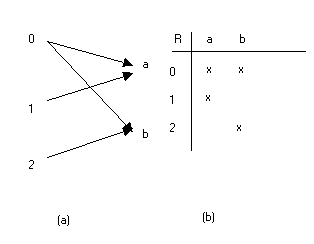

รูปที่ 1 แสดงการจัดระเบียบแบบคู่ ในความสัมพันธ์ R จากตัวอย่างที่ 3

นิยาม 2 ความสัมพันธ์บนเซต A คือ ความสัมพันธ์จาก A ไป A

หรือความสัมพันธ์บนเซต A คือซับเซตของ A ด A

ตัวอย่างที่ 4 ให้ A เป็นเซต {1, 2, 3,4} R เป็นความสัมพันธ์บน A กำหนดโดย

R = {(a,b) | a / b } จงเขียนความสัมพันธ์ R แบบแจกแจงสมาชิก

วิธีทำ (a,b) อยู่ใน R ก็ต่อเมื่อ a และ b เป็นจำนวนเต็มบวกที่มีค่าไม่เกิน 4 และ a / b

ดังนั้น R = {(1,1), (1,2), (1,3), (1,4), (2,2), (2,4), (3,3), (4,4)}

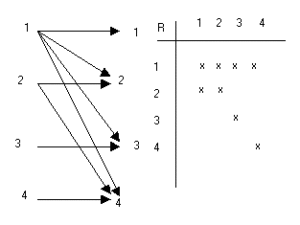
รูปที่ 2 เป็นกราพ และ ตาราง แสดงความสัมพันธ์ R จากตัวอย่างที่ 4

ตัวอย่างที่ 5 พิจารณาความสัมพันธ์บนเซตของจำนวนเต็ม ต่อไปนี้

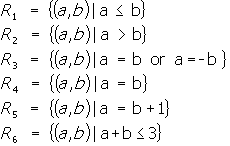
อยากทราบว่าคู่อันดับต่อไปนี้อยู่ในความสัมพันธ์ใดบ้าง
(1,1), (1,2), (2,1), (1, -1) และ (2,2)

วิธีทำ

คู่ลำดับ (1,1) อยู่ใน R₁ ,R₃ , R₄ และ R₆
คู่ลำดับ (1,2) อยู่ใน R₁ และ R₆
คู่ลำดับ (2,1) อยู่ใน R₂, R₅ และ R₆
คู่ลำดับ (1,-1) อยู่ใน R₂ ,R₃ และ R₆
ท้ายสุดคู่ลำดับ (2,2) อยู่ใน R₁ ,R₃ และ R₄ตัวอย่างที่ 6 จงหาจำนวนความสัมพันธ์ บนเซตที่มีสมาชิก n ตัว

วิธีทำ

จากความสัมพันธ์บนเซต A เป็นสับเซตของ A X A
และจากสมาชิกของ A XA มีค่าเท่ากับ n² เมื่อ A มีค่า เท่ากับ n ดังนั้นจำนวนเซตที่
เป็นเซตย่อยของ มีค่าเป็น 
นั่นคือ จำนวนความสัมพันธ์บนเซต A จึงมีทั้งหมด ความสัมพันธ์