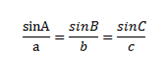ฟังก์ชั่นไซน์และโคไซน์
ฟังก์ชันไซน์และโคไซน์
การกำหนดค่าของฟังก์ชันตรีโกณมิตินั้น สามารถทำได้โดยการใช้วงกลมรัศมี 1 หน่วย มีจุดศูนย์กลางอยู่ที่จุดกำเนิด และเราจะเรียกวงกลมดังกล่าวว่า วงกลมหนึ่งหน่วย (The unit circle)
เมื่อเรากำหนดจำนวนจริง θ (ทีตา) จาก (1,0) วัดระยะไปตามส่วนโค้งของวงกลม โดยมีข้อตกลงดังนี้ว่า :
ถ้า θ > 0 จะวัดส่วนโค้งจากจุด (1,0) ไปในทิศทางทวนเข็มนาฬิกา
ถ้า θ < 0 จะวัดส่วนโค้งจากจุด (1,0) ไปในทิศทางตามเข็มนาฬิกา
ถ้า θ = 0 จุดปลายส่วนโค้งคือจุด (1,0)
จะได้ว่า เมื่อเรากำหนดจำนวนจริง θ ให้ เราสามรารถหาจุด (x,y) ซึ่งเป็นจุดปลายส่วนโค้งได้เพียงจุดเดียวเท่านั้น
ถ้า |θ| > 2π แสดงว่า วัดส่วนโค้งเกิน 1 รอบ เพราะเส้นรองวงของวงกลมยาว 2π หน่วย
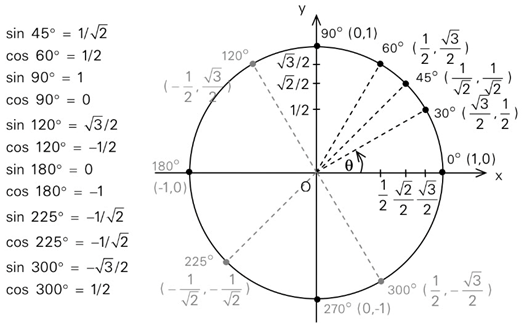
เมื่อ (x,y) เป็นจุดปลายส่วนโค้งของวงกลมข้างต้น
y = sin θ (อ่านว่า วาย เท่ากับ ไซน์ทีตา)
x = cos θ (อ่านว่า เอกซ์ เท่ากับ คอสทีตา)
ฟังก์ชันไซน์และฟังก์ชันโคไซน์นั้น เป็นจำนวนจริง ตั้งแต่ –1 ถึง 1
นั่นคือ เรนจ์ของฟังก์ชันไซน์และโคไซน์ คือ เซตของจำนวนจริง ตั้งแต่ –1 ถึง 1 และโดเมนของฟังก์ชันทั้งสองคือเซตของจำนวนจริง
จากสมการ x2 + y2 = 1 , y = sin θ , x = cos θ จะได้ความสัมพันธ์ของ sin θ และ cos θ ดังนี้
(cos θ)2 + (sin θ)2 = 1 เมื่อ θ เป็นจำนวนจริง
หรือเขียนได้เป็น
cos2 θ + sin2 θ = 1 เมื่อ θ เป็นจำนวนจริง
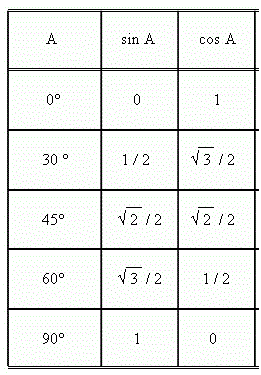
ค่าของฟังก์ชันไซน์และโคไซน์
ค่าของฟังก์ชันไซน์และโคไซน์ เป็นดังตารางนี้
พิจารณาจำนวนจริง θ > 0 และ (x,y) เป็นจุดปลายส่วนโค้งของวงกลมหนึ่งหน่วยที่วัดจากจุด (1,0) ไปในทิศทางทวนเข็มนาฬิกา ยาว θหน่วย (เนื่องจาก θ > 0 จึงได้ |θ| = θ ) จากการให้จุด (x,-y) เป็นภาพสะท้อนที่เกิดจากการสะท้อนจุด (x,y) โดยมีแกน X เป็นเส้นสะท้อนจึงได้จุด (x,-y) เป็นจุดปลายส่วนโค้งของวงกลมดังกล่าวที่วัดจากจุด (1,0) ไปในทิศทางตามเข็มนาฬิกายาว θ หน่วย หรือกล่าวได้ว่า (x,-y) เป็นจุดปลายของส่วนโค้งที่เกิดจากจำนวนจริง -θ
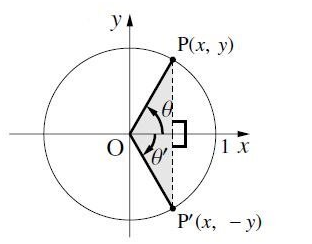
จากจุด (x,y) และ (x,-y) ทำให้สรุปได้ว่า
x = cos θ , y = sin θ
และ x = cos (-θ) , -y = sin (-θ)
ดังนั้น
sin (-θ) = -sin θ
cos (-θ) = cos θ
กฎของโคไซน์ และไซน์
กฎของโคไซน์ ในรูปสามเหลี่ยม ABC ใดๆ ถ้า a, b และ c เป็นความยาวของด้านตรงข้ามมุม A, B และ C ตามลำดับ
จะได้
a2 = b2 + c2 – 2bc cosA
b2 = c2 + a2 – 2ca cosB
c2 = a2 + b2 – 2ab cosC
กฎของไซน์ ในรูปสามเหลี่ยม ABC ใดๆ ถ้า a,b และ c เป็นความยาวของด้านตรงข้ามมุม A,B และ C ตามลำดับ
จะได้