ทฤษฏีกราฟเบื้องต้น
ดีกรีของจุดยอด
|
จุดยอด |
จำนวนครั้งทั้งหมดที่เส้นเชื่อมเกิดกับจุดยอด |
|
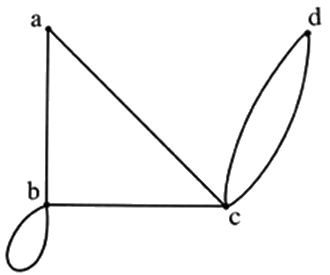
a b c d |
2 4 4 2 |
จะเห็นว่า เส้นเชื่อมที่เกิดกับจุดยอด a ได้แก่ เส้นเชื่อม ab และ ac ดังนั้น จำนวนครั้งทั้งหมดที่เส้นเชื่อมเกิดกับจุดยอด a
คือ 2 สำหรับจุดยอด b มีเส้นเชื่อมที่เกิดกับจุดยอด b ได้แก่ เส้นเชื่อม ba, bc และ bb เป็นวงวน เกิดกับจุดยอด b
กรณีที่มีเส้นเชื่อมเป็นวงวน จะกำหนดให้นับจำนวนเส้นเชื่อมที่เกิดกับจุดยอดนั้นเพิ่มขึ้น โดยให้นับเส้นเชื่อมที่เป็นวงวน 1 วง วงวนเป็น 2 ดังนั้นจำนวนครั้งทั้งหมดที่เส้นเชื่อมเกิดกับจุดยอด b จึงเป็น 4
|
ทฤษฎีบท 1
ผลรวมของดีกรีของจุดยอดทุดจุดในกราฟเท่ากับสองเท่าของจำนวนเส้นเชื่อมในกราฟ
|
เนื่องจากเส้นเชื่อมแต่ละเส้นในกราฟเกิดกับจุดยอดเป็นจำนวน 2 ครั้ง ดังนั้นเส้นเชื่อมแต่ละเส้นจะถูกนับ 2 ครั้งในผลรวมของดีกรีของจุดยอดทุกจุด
นั่นคือ ผลรวมของดีกรีของจุดยอดทุกจุดในกราฟเท่ากับสองเท่าของจำนวนเส้นเชื่อมในกราฟ
|
บทนิยาม
จุดยอดที่มีดีกรีเป็นจำนวนคู่ เรียกว่า จุดยอดคู่ (Even Vertex)
จุดยอดที่มีดีกรีเป็นจำนวนคี่ เรียกว่า จุดยอดคี่ (Odd Vertex)
|
|
ทฤษฎีบท 2 ทุกกราฟจะมีจุดยอดคี่เป็นจำนวนคู่
|
ดังนั้น ดีกรี (degree) ของจุดยอด v ในกราฟคือ จำนวนครั้งทั้งหมดที่เส้นเชื่อมเกิดกับจุดยอด v ใช้สัญลักษณ์ deg v แทนดีกรีของจุดยอด v
ดังนั้นจะได้ว่า
| deg | sub |
| deg a
deg b deg c deg d |
2
4 4 2 |
ขอขอบพระคุณข้อมูลบางส่วนจากเว็บไซต์ http://www.vcharkarn.com/






