การอธิบายปรากฏการณ์ธรรมชาติ
– ในสมัยโบราณ มนุษย์เชื่อว่าปรากฏการณ์ที่เกิดขึ้นในธรรมชาติเกิดขึ้นจาก เทพเจ้า หรือสิ่งศักดิ์สิทธิ์ การอธิบายปรากฏการณ์ต่างๆ ที่เกิดขึ้น ยังไม่มีความเป็นเหตุเป็นผล
– ยุคต่อมาเริ่มมีการสังเกตุและบันทึกข้อมูลเกี่ยวกับสิ่งที่ศึกษา เพื่ออธิบายปรากฏการณ์ธรรมชาติต่างๆ ทำให้เกิดการพัฒนาความรู้ของมนุษย์
– สรุปได้ว่า การพัฒนาความรู้ของมนุษย์ เกิดจากการสังเกตุ การบันทึกข้อมูล และการวิเคราะห์ข้อมูลที่ได้เพื่อสรุปเป็นความรู้และมองเห็นความสัมพันธ์ในเชิงคณิตศาสตร์ระหว่างสิ่งต่างๆและความสัมพันธ์ระหว่างเรื่อง
ลักษณะปรากฏการณ์ทางธรรมชาติที่สำคัญและการป้องกันอันตราย
ฟิสิกส์
– ฟิสิกส์ เป็นวิชาที่ศึกษาหากฏเกณฑ์ต่างๆ สำหรับอธิบายปรากฏการณ์ในธรรมชาติ ความสัมพันธ์ระหว่างสสารและพลังงาน
– นักฟิสิกส์จะนำข้อมูลที่ได้มาวิเคราะห์แปลความหมายลงข้อสรุปเป็นหลักการและกฏเกณฑ์ต่างๆ
– ความรู้ในวิชาฟิสิกส์ ส่วนหนึ่งได้มาจากข้อมูลจากการสังเกตุและการวัดโดยอาศัยเครื่องมือและอุปกรณ์ต่างๆ
– ความรู้อีกส่วนหนึ่งได้มาจากแบบจำลองทางความคิด ซึ่งนำมาสู่การสร้างทฤษฎีเพื่ออธิบายปรากฏการณ์ธรรมชาติ
– ความรู้ทางฟิสิกส์เกี่ยวข้องกับศาสตร์ต่างๆ มากมาย รวมทั้งเป็นพื้นฐานให้เกิดเทคโนโลยี
– ความรู้ที่เป็นพื้นฐานฟิสิกส์ได้แก่ กลศาสตร์ ความร้อน แสง เสียง ไฟฟ้า แม่เหล็ก ฟิสิกส์อะตอม และ ฟิสิกส์นิวเคลียร์
1.3 ปริมาณกายภาพ และ หน่วย
– ปริมาณกายภาพ เป็น ปริมาณที่สามารถวัดได้ด้วยเครื่องมือโดยตรงหรือโดยอ้อม
– เป็นปริมาณที่มีความหมายเฉพาะเจาะจง และ มีหน่วยกำกับจึงจะมีความหมายชัดเจน เช่น มวล หน่วยเป็น กิโลกรัม ความยาว หน่วยเป็น เมตร
– หน่วยมาตรฐานที่ใช้ในวงการวิทยาศาสตร์ทั่วโลก เรียกว่า “ระบบหน่วยระหว่างชาติ (The International System of Unit : SI Unit)
– หน่วยในระบบ เอสไอ ประกอบด้วย หน่วยฐาน และ หน่วยอนุพันธ์
-หน่วยฐาน มี 7 ปริมาณ ซึ่งมีหน่วยของปริมาณ และสัญญลักษณ์ของหน่วย ดังนี้
| ปริมาณ | หน่วย | สัญญลักษณ์ |
| ความยาว | เมตร | m |
| มวล | กิโลกรัม | kg |
| เวลา | วินาที | s |
| กระแสไฟฟ้า | แอมแปร์ | A |
| อุณหภูมิ | เคลวิน | K |
| ความเข้มของการส่องสว่าง | แคนเดลา | cd |
| ปริมาณของสาร | โมล | mol |
– หน่วยอนุพันธ์ เป็นหน่วยที่เกิดจากหน่วยฐานหลายหน่วย เช่นปริมาณ “แรง” มีหน่วยเป็น newton ใช้สัญญลักษณ์ N เกิดจากหน่วยฐาน ( Kg. m ) / s2
คำนำหน้าหน่วย
คำนำหน้าหน่วย เป็นคำที่เมื่อนำมาวางหน้าหน่วยแล้ว จะทำให้หน่วยใหญ่ขึ้น หรือ เล็กลง เช่น
K เมื่อนำมาวางหน่วย g —> จะทำให้หน่วย g เป็น Kg ซึ่งมีขนาดใหญ่ขึ้น 1000 เท่า ตามค่าของ K
m เมื่อนำมาวางหน่วย g —> จะทำให้หน่วย g เป็น mg ซึ่งมีขนาดเล็กลง 0.001 เท่าตามค่าของ m
คำนำหน้าหน่วย ที่สำคัญและใช้บ่อย มีดังนี้
| คำอุปสรรค | สัญลักษณ์ | ตัวคูณ |
| เทระ(tera) | T | 1012 |
| จิกะ(giga) | G | 109 |
| เมกะ(mega) | M | 106 |
| กิโล(kilo) | k | 103 |
| เฮกโต(hecto) | h | 102 |
| เดคา(deca) | da | 101 |
| เดซิ(deci) | d | 10-1 |
| เซนติ(centi) | c | 10-2 |
| มิลลิ(milli) | m | 10-3 |
| ไมโคร(micro) | μ | 10-6 |
| นาโน(nano) | n | 10-9 |
| พิโค(pico) | p | 10-12 |
1.4 การทดลองในวิชาฟิสิกส์
การทดลองในวิชาฟิสิกส์ที่มีในบทเรียน เป็นการทดลองเพื่อตอบคำถาม หรือหาความจริงบางอย่าง ซึ่งวิธีทดลองได้ออกแบบตามเครื่องมือหรืออุปกรณ์ มีการนำเสนอข้อมูลจากการทดลอง การวิเคราะห์ การแปลผล และลงข้อสรุป เพื่อให้เกิดความเข้าใจ และเรียนรู้ ตามจุดประสงค์ของการทดลองนั้นๆ
1.5 ความไม่แน่แน่นอนในการวัด
เพื่อให้ผลการวัด ได้ค่าที่เหมาะสมใกล้เคียงความเป็นจริงที่สุด ผู้วัดจะต้องใช้เครื่องมือที่เหมาะสมกับสิ่งที่ต้องการวัด นอกจากนี้ประสบการณ์และความสามารถของผู้วัดก็เป็นปัจจัยสำคัญที่จะทำให้ผลการวัดมีความคลาดเคลื่อนน้อยที่สุดด้วย
1.6 เลขนัยสำคัญ
ซึ่งขอขอบคุณ มา ณ ที่นี้
1.6.1 ผลของการวัดและเลขนัยสำคัญ
ผลของการวัดที่ได้จากเครื่องมือวัดโดยตรง ผู้วัดต้องอ่านค่าจากส่วนแสดงผลที่เครื่องวัด
ในการอ่านค่าเครื่องวัดที่เป็นขีดสเกล จะต้องทราบค่าละเอียดที่สุดที่เครื่องวัดนั้นสามารถอ่านค่าได้ แล้วประมาณค่าในตำแหน่งถัดไป เพื่อให้ได้ผลการวัดใกล้กับความเป็นจริงมากที่สุด เช่น การวัดค่าความยาวของแท่งโลหะด้วยไม้บรรทัด ดังรูป
![]()
จากรูปไม้บรรทัดมีสเกลเล็กที่สุดเท่ากับ 1 cm จึงสามารถอ่านค่าได้ละเอียดที่สุดเพียงหน่วยเซนติเมตรเท่านั้น จากนั้นประมาณค่าทศนิยมตำแหน่งที่ 1 นั่นคือการวัดความยาวของแท่งเหล็กได้ 2.2 cm

ไม้บรรทัดนี้มีสเกลเล็กสุดเท่ากับ 1 mm หรือ 0.1 cm ค่าละเอียดที่สุดที่สามารถอ่านได้คือทศนิยมตำแหน่งที่ 1 ของเซนติเมตร และประมาณค่าตัวเลขหลังทศนิยมตำแหน่งที่ 2 ดังนั้นวัดความยาวของแท่งโลหะได้ 2.27 cm
การแสดงความเที่ยงตรงของผลการวัดที่ได้จากการวัดโดยตรง หรือผลที่คำนวณมาจากผลการวัดจะใช้คำเรียกว่า “เลขนัยสำคัญ” (Significant Figure) ซึ่งประกอบด้วยตัวเลขที่แสดงความแน่นอนรวมกับตัวเลขที่แสดงความไม่แน่นอน
1.6.2 การนับเลขนัยสำคัญ
การนับจำนวนหรือตำแหน่งของเลขนัยสำคัญ แสดงในตาราง
| หลักการ | ตัวอย่าง | จำนวนเลขนัยสำคัญ |
| 1 ตัวเลขที่ไม่มีเลขศูนย์ ตัวเลขทั้งหมดนับเป็นเลขนัยสำคัญ | 5.78 | 3 ตำแหน่ง |
| 2 เลขศูนย์ที่อยู่หน้าตัวเลขอื่น ๆ ไม่นับเป็นเลขนัยสำคัญ | 0.45
0.000357 |
2 ตำแหน่ง
3 ตำแหน่ง |
| 3 เลขศูนย์ที่อยู่หลังหรือระหว่างตัวเลขอื่นที่ไม่ใช่เลขศูนย์ นับเป็นเลขนัยสำคัญ | 14000.00
0.1009 |
7 ตำแหน่ง
4 ตำแหน่ง |
| 4 สัญกรณ์ทางวิทยาศาสตร์ ให้นับเฉพาะส่วนที่เป็นตัวเลข ไม่นับเลขยกกำลังฐาน 10 | 5.83 x 10-6 | 3 ตำแหน่ง |
| 5 จำนวนที่มีค่าน้อยมาก ๆ หรือค่าใหญ่มาก ๆ นิยมเขียนในรูปสัญกรณ์ทางวิทยาศาสตร์ก่อน แล้วนับเลขนัยสำคัญ | 298000
2.98 x 105 |
3 ตำแหน่ง |
1.6.3 เลขนัยสำคัญที่ได้จากผลการวัดโดยตรง
เลขนัยสำคัญที่ได้จากผลของการวัดอาจเป็นเลขจำนวนเต็มหรือเป็นเลขทศนิยม ขึ้นอยู่กับความละเอียดของเครื่องมือที่ใช้วัด โดยจะประกอบด้วยตัวเลขที่ได้จากการอ่านค่าจากเครื่องมือ บวกกับตัวเลขที่ได้จากการประมาณค่า
เลขนัยสำคัญ = เลขจากการอ่านค่า + เลขจากการประมาณค่า เช่น
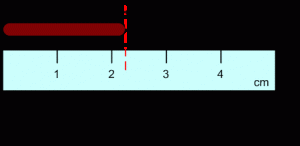
อ่านค่าได้เท่ากับ 2 + 0.2 = 2.2 cm
เลขนัยสำคัญ 2 ตำแหน่ง
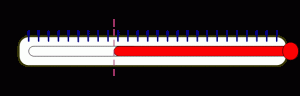
อ่านค่าได้เท่ากับ 32 + 0.2 = 32.2 °C
เลขนัยสำคัญ 3 ตำแหน่ง

อ่านค่าได้เท่ากับ 2.2 + 0.07 = 2.27 cm
เลขนัยสำคัญ 3 ตำแหน่ง
1.7 การระบุจำนวนเลขนัยสำคัญของผลลัพธ์ที่ได้จากการคำนวณ
มีวิธีการดังนี้
1) ผลลัพธ์จากการบวกและลบ ต้องมีจำนวนเลขทศนิยมเท่ากับข้อมูลที่มีเลขทศนิยมน้อยที่สุด
2) ผลลัพธ์จากการคูณและหาร ต้องมีจำนวนเลขนัยสำคัญเท่ากับข้อมูลที่เลขนัยสำคัญน้อยที่สุด
3) ข้อมูลที่มาจากการนับหรือการเทียบหน่วยในระบบเดียวกัน ไม่นำมาพิจารณาจำนวนเลขนัยสำคัญ
1.8 การปัดเศษ เลขนัยสำคัญที่ได้จากการคำนวณ
ในการคำนวณ ผลที่ได้จากการคำนวณมักมีตัวเลขทศนิยมหลายตำแหน่ง ทำให้มีจำนวนเลขนัยสำคัญมากกว่าที่ควรเป็น จึงต้องตัดตัวเลขทศนิยมตำแหน่งที่เกินออกไป
โดยใช้การปัดเศษ (rounding off)
ซึ่งเริ่มจากการหาตัวเลขตำแหน่งสุดท้ายของเลขนัยสำคัญที่ต้องการ แล้วปัดเศษตัวเลขทศนิยมตำแหน่งถัดไปทางขวา จากหลักการต่อไปนี้
1) ถ้าตัวเลขที่ต้องการปัดเศษต่ำกว่า 5 ให้ปัดลง โดยตัวตัวเลขนั้นออกไป ส่วนเลขสุดท้ายของตำแหน่งที่ต้องการยังคงเป็นตัวเลขเดิม
2) ถ้าตัวเลขที่ต้องการปัดเศษมากกว่ากว่า 5 ให้ปัดขึ้น โดยตัดตัวเลขนั้นออกไป แล้วเพิ่มค่าของตัวเลขตัวสุดท้ายของตำแหน่งที่ต้องการอีก 1
3) ถ้าตัวเลขที่ต้องการปัดเศษมีค่าเท่ากับ 5 ให้พิจารณาตัวเลขตัวสุดท้ายของตำแหน่งที่ต้องการ ถ้าเป็นเลขคี่ให้ปัดขึ้น แต่ถ้าเป็นเลขคู่ให้ปัดลง เช่น
– จงทำให้จำนวน 86.583219 มีเลขนัยสำคัญ 4 ตำแหน่ง
ตัวเลขตัวสุดท้ายของเลขนัยสำคัญตำแหน่งที่ 4 คือ 8 ดังนั้นตัวเลขที่ต้องการปัดเศษคือ 3 ซึ่งมีค่าน้อยกว่า 5 จึงปัดลง โดยการตัดตัวเลขหลัง 8 ทิ้งไป จะได้จำนวนเลขนัยสำคัญ 4 ตำแหน่ง เป็น 86.58
– จงทำให้จำนวน 75.9876 มีเลขนัยสำคัญ 4 ตำแหน่ง
ตัวเลขตัวสุดท้ายของเลขนัยสำคัญตำแหน่งที่ 4 คือ 8 ดังนั้นตัวเลขที่ต้องการปัดเศษคือ 7 ซึ่งมีค่ามากกว่า 5 จึงปัดขึ้น โดยตัดตัวเลขหลัง 8 ออก แล้วเพิ่มค่าของ 8อีก 1 จะได้จำนวนที่มีเลขนัยสำคัญ 4 ตำแหน่ง เป็น 75.99
– จงทำให้จำนวน 2.635 มีเลขนัยสำคัญ 3 ตำแหน่ง
ตัวเลขตัวสุดท้ายของเลขนัยสำคัญตำแหน่งที่ 3 คือ 3 ดั้งนั้นตัวเลขที่ต้องการปัดเศษคือ 5 จึงพิจารณาตัวเลขตัวสุดท้ายของตำแหน่งที่ต้องการคือ 3 ซึ่งเป็นเลขคี่ จึงปัดขึ้น โดยตัดตัวเลขหลัง 3 ออกแล้วเพิ่มจำนวน 3 อีกหนึ่ง จะได้จำนวนที่มีเลขนัยสำคัญ 3 ตำแหน่ง เป็น 2.64
– จงทำให้จำนวน 27.4865 มีเลขนัยสำคัญ 5 ตำแหน่ง
ตัวเลขตัวสุดท้ายของเลขนัยสำคัญตำแหน่งที่ 5 คือ 6 ดั้งนั้นตัวเลขที่ต้องการปัดเศษคือ 5 จึงพิจารณาตัวเลขตัวสุดท้ายของตำแหน่งที่ต้องการคือ 6 ซึ่งเป็นเลขคู่ จึงปัดลง โดยตัดเลข 5 ทิ้ง จะได้จำนวนที่มีเลขนัยสำคัญ 5 ตำแหน่ง เป็น 27.486
– หาคำตอบของ
53.27 m + 16.8 m
จำนวนที่มีเลขทศนิยมน้อยที่สุด คือ 16.8 มีเลขทศนิยม 1 ตำแหน่ง คำนวณข้อมูลแล้วปัดเศษผลลัพธ์ให้มีเลขทศนิยม 1 ตำแหน่ง
53.27 m + 16.8 m = 70.07 m
ตอบ = 70.1 m
– หาคำตอบของ
0.9387 mm x 1.542 mm x 1.32 mm
จำนวนที่มีเลขนัยสำคัญน้อยที่สุด คือ 1.32 ซึ่งมีเลขนัยสำคัญ 3 ตำแหน่ง คำนวณข้อมูลแล้วปัดเศษผลลัพธ์ให้มีเลขนัยสำคัญ 3 ตำแหน่ง
0.9387 mm x 1.542 mm x 1.32 mm = 2.7656 mm3
ตอบ = 2.76 mm3
– หาคำตอบของ
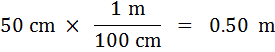
จำนวน 1 m และ 100 cm เป็นข้อมูลที่ได้จากการเทียบหน่วยในระบบเดียวกัน จึงไม่นำมาพิจารณาเลขนัยสำคัญ ดังนั้นพิจารณาเฉพาะ 50 cm ซึ่งมีเลขนัยสำคัญ 2 ตำแหน่ง
– หาคำตอบของ
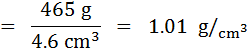
คำนวณข้อมูลที่เป็นการลบก่อนแล้วจึงนำไปหาร โดยอาศัยหลักเลขนัยสำคัญในแต่ละขั้นตอนด้วย ดังนั้นผลที่ได้จาการลบต้องมีทศนิยม 1 ตำแหน่ง
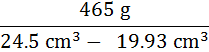
เมื่อหารแล้วผลลัพธ์ที่ได้ต้องมีเลขนัยสำคัญ 2 ตำแหน่ง
ตอบ = 1.0 g/cm3






