พื้นที่ พื้นที่ผิว และปริมาตร

ปริซึม
สิ่งของรอบๆ ตัวเราหลายอย่างมีลักษณะเป็นปริซึม เช่น กล่องยาสีฟันมีลักษณะเป็นปริซึมสี่เหลี่ยม กล้องสลับลายมีลักษณะเป็นปริซึมสามเหลี่ยม รวมถึงของใช้ในชีวิตประจำวันอีกมากมาย
ในทางคณิตศาสตร์ปริซึมมีลักษณะ ดังนี้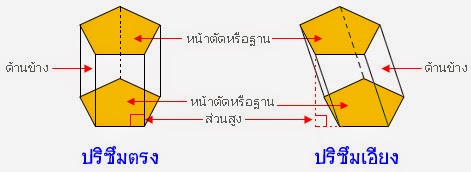

รูปเรขาคณิตสามมิติที่มีฐานทั้งสองเป็นรูปเหลี่ยมที่เท่ากันทุกประการ ฐานทั้งสองอยู่บน
ระนาบที่ขนานกัน และด้านข้างแต่ละด้านเป็นรูปสี่เหลี่ยมด้านขนาน เรียกว่า ปริซึม

ส่วนต่างๆ ของปริซึมมีชื่อเรียก ดังนี้

เราเรียกชื่อปริซึมชนิดต่างๆ ตามลักษณะของฐานของปริซึม ดังตัวอย่าง

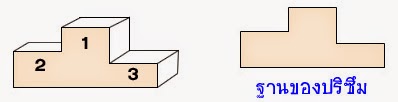
นอกจากปริซึมที่มีฐานเป็นรูปเหลี่ยมแล้ว เราอาจพบปริซึมที่มีฐานเป็นรูปเหลี่ยมชนิดใดๆ ก็ได้ เช่น แท่นรับรางวัล

ถึงแม้ว่าจะมีทั้งปริซึมตรงและปริซึมเอียง แต่ในบทเรียนนี้จะกล่าวถึงปริซึมตรงที่มีด้านข้างตั้งฉากกับฐานเท่านั้น จะไม่กล่าวถึงปริซึมเอียงที่มีด้านข้างไม่ตั้งฉากกับฐาน

ทรงกระบอก

ทรงกระบอกเป็นรูปเรขาคณิตสามมิติที่มีรูปร่างคล้ายกระบอกไม้ไผ่ที่ตัดเป็นท่อน มีหลายสิ่งที่มีคำว่ากระบอกอยู่ในชื่อ เพื่อบ่งบอกให้รู้ว่ามีส่วนเกี่ยวข้องกับทรงกระบอก เช่น เสื้อแขนกระบอก หุ่นกระบอก หรือปลากระบอก นอกจากนี้รอบๆ ตัวเรายังมีสิ่งของอีกหลายสิ่งที่ส่วนประกอบมีลักษณะเป็นทรงกระบอก เช่น แก้วน้ำ แจกัน หลอดยาดม และถ่านไฟฉาย

ในทางคณิตศาสตร์ ทรงกระบอกมีลักษณะ ดังนี้

รูปเรขาคณิตสามมิติที่มีฐานสองฐานเป็นรูปวงกลมที่เท่ากันทุกประการ
และอยู่บนระนาบที่ขนานกัน และเมื่อตัดรูปเรขาคณิตสามมิตินั้น
ด้วยระนาบที่ขนานกับฐานแล้วจะได้หน้าตัดที่เป็นวงกลมเท่าๆ
กันทุกประการกับฐานเสมอ เรียกรูปเรขาคณิตสามมิตินั้นว่า ทรงกระบอก

รูปด้านล่างนี้เป็นรูปของทรงกระบอกและส่วนต่างๆ ของทรงกระบอก

ในบทเรียนนี้จะกล่าวถึงเฉพาะทรงกระบอกที่มีแกนตั้งฉากกับฐานเท่านั้น

พีระมิด
ในชีวิตประจำวัน น้องๆ อาจจะพบกับสิ่งก่อสร้างที่ส่วนประกอบมีลักษณะเป็นพีระมิด เช่น หลังคายอดโดมของมหาวิทยาลัยธรรมศาสตร์ หลังคาบ้านและอาคารต่างๆ ดังรูป

โดยทั่วไปเมื่อกล่าวถึงคำว่าพีระมิด เรามักนึกถึงและเข้าใจว่าพีระมิดจะต้องมีฐานเป็นรูปสี่เหลี่ยมจัตุรัสเช่นเดียวกันกับฐานของพีระมิดในประเทศอียิปต์เสมอ แต่ในทางคณิตศาสตร์แล้วฐานของพีระมิดไม่จำเป็นต้องมีรูปสี่เหลี่ยมจัตุรัสก็ได้

ในทางคณิตศาสตร์ พีระมิดมีลักษณะดังนี้

รูปเรขาคณิตสามมิติที่มีฐานเป็นรูปเหลี่ยมใดๆ มียอดแหลมที่ไม่อยู่ในระนาบเดียวกันกับฐาน และหน้าทุกหน้าเป็นรูปสามเหลี่ยมที่มีจุดยอดร่วมกันที่ยอดแหลมนั้น เรียกว่า พีระมิด

ในทางคณิตศาสตร์พีระมิดตรงเป็นพีระมิดที่มีฐานเป็นรูปหลายเหลี่ยมด้านเท่ามุมเท่า และมีสันทุกสันยาวเท่ากัน
เราเรียกพีระมิดชนิดต่างๆ ตามลักษณะของฐานของพีระมิด ดังตัวอย่าง

ในบทเรียนนี้จะกล่าวถึงพีระมิดฐานตรงและพีระมิดที่มีสันทุกสันยาวเท่ากันเท่านั้น

กรวย
สิ่งต่างๆ ที่ประกอบมีลักษณะเป็นกรวย ส่วนใหญ่เป็นสิ่งที่มนุษย์สร้างขึ้น เช่น กระโจม โคมไฟ กรวยจราจร หมวก และกระทงใบตองที่ฝามีลักษณะเป็นกรวย นอกจากนี้ กรวยยังเป็นชื่อขนมชนิดหนึ่งที่ทำจากแป้งข้าวเจ้า กะทิ และน้ำตาลปีบ บรรจุอยู่ในกรวยใบตอง

ในทางคณิตศาสตร์ กรวยมีลักษณะดังนี้

รูปเรขาคณิตสามมิติที่มีฐานเป็นรูปวงกลม มียอดแหลมที่ไม่อยู่บนระนาบเดียวกับฐาน
และเส้นที่ต่อระหว่างจุดยอดและจุดใดๆ บนขอบของฐานเป็นส่วนของเส้นตรง
เรียกรูปเรขาคณิตสามมิตินั้นว่า กรวย

รูปข้างล่างนี้เป็นรูปของกรวยและส่วนต่างๆ ของกรวย

ในบทเรียนนี้จะกล่าวถึงเฉพาะกรวยตรงที่มีส่วนสูงยาวเท่ากับความยาวของแกนเท่านั้น

ทรงกลม
ทรงกลมเป็นรูปเรขาคณิตสามมิติอีกชนิดหนึ่งที่น้องๆ อาจจะคุ้นเคยดี และเป็นสิ่งที่มนุษย์สร้างขึ้น และสิ่งมีชีวิตทั้งพืช สัตว์ ตลอดจนจุลชีพที่ไม่สามารถเห็นได้ด้วยตาเปล่า เช่น ลูกเทนนิส ลูกแก้ว ลูกบอล และผลไม้ลูกกลมๆ

ในทางคณิตศาสตร์ทรงกลมมีลักษณะดังนี้

รูปเรขาคณิตสามมิติที่มีผิวโค้งเรียบ และจุดทุกจุดบนผิวโค้งอยู่ห่าง
จากจุดคงที่จุดหนึ่งเป็นระยะเท่ากัน เรียกว่า ทรงกลม

จุดคงที่นั้นเรียกว่า จุดศูนย์กลางของทรงกลม
ระยะที่เท่ากันนั้นเรียกว่า รัศมีของทรงกลม

เมื่อตัดทรงกลมด้วยระนาบผ่านจุดศูนย์กลางของทรงกลม จะได้หน้าตัดเป็นวงกลมเรียกว่า วงกลมใหญ่

ปริมาตรของปริซึมและทรงกระบอก

บุคคลในหลายสาขาอาชีพต้องเข้าใจและชำนาญในเรื่องของการวัด การชั่ง การตวง และเรื่องที่เกี่ยวกับปริมาตรเป็นอย่างดี ไม่เช่นนั้นอาจทำให้เกิดข้อผิดพลาดและเสียหาย เช่น วิศวกรอาจออกแบบโครงสร้างของสิ่งก่อสร้างต่างๆ ได้ไม่แข็งแรงพอ นักวิทยาศาสตร์อาจทำการทดลองแล้วผิดพลาดทำให้เกิดการระเบิด หรือพ่อครัวอาจปรุงรสอาหารแล้วได้รสชาติไม่คงที่

สำหรับบุคคลทั่วไป การเรียนรู้และใช้ความรู้เกี่ยวกับปริมาตรจะช่วยให้เราเป็นผู้บริโภคที่ฉลาดในการเลือกซื้อสินค้า รู้จักเปรียบเทียบราคาของสินค้าต่อหน่วยปริมาตร ทำให้เลือกซื้อสินค้าได้ถูกว่าและช่วยให้เราประหยัดค่าใช้จ่ายได้

เมื่อกล่าวถึงการวัดความจุ จะหมายถึงการหาปริมาตร การหาปริมาตรของวัตถุใดๆ อาจทำได้โดยการจมวัตถุนั้นลงในภาชนะที่มีน้ำอยู่ ตราบใดที่วัตถุไม่ละลายหรือดูดซับน้ำ ปริมาตรของน้ำส่วนที่เพิ่มขึ้น หรือปริมาตรของน้ำที่ล้นออกมาในกรณีเดิมมีน้ำอยู่เต็มภาชนะพอดี จะเท่ากับปริมาตรของวัตถุนั้น วิธีการนี้เป็นการหาปริมาตรของวัตถุโดยการแทนที่น้ำ

ในทางคณิตศาสตร์ เราอาจคำนวณหาปริมาตรของสิ่งของต่างๆ ได้โดยไม่ต้องใช้การแทนที่น้ำ ในบทเรียนนี้ น้องๆ จะได้ศึกษาการหาปริมาตรของรูปเรขาคณิตสามมิติหลายชนิด ได้แก่ ปริซึม ทรงกระบอก พีระมิด และทรงกลม

ปริมาตรของปริซึม
ทรงสี่เหลี่ยมมุมฉากเป็นปริซึมชนิดหนึ่งที่เรียกว่า ปริซึมสี่เหลี่ยมมุมฉาก น้องๆ รู้จักการหาปริมาตรของทรงสี่เหลี่ยมมุมฉากมาแล้ว ดังนั้น สูตรการหาปริมาตรของปริซึมสี่เหลี่ยมมุมฉาก จึงเป็นสูตรเดียวกันกับสูตรการหาปริมาตรของทรงสี่เหลี่ยมมุมฉาก กล่าวคือ

ปริมาตรของปริซึมสี่เหลี่ยมมุมฉาก	=	ความกว้าง x ความยาว x ความสูง
	=	พื้นที่ฐาน x ความสูง

สำหรับปริมาตรของปริซึมสามเหลี่ยมใดๆ หาได้โดยอาศัยวิธีหาปริมาตรของปริซึมสามเหลี่ยมมุมฉาก ดังนี้
ปริมาตรของปริซึมสามเหลี่ยมมุมฉาก = ½ ของปริมาตรของปริซึมสี่เหลี่ยมมุมฉาก

จากความจริงข้างต้น ช่วยให้เราหาปริมาตรของปริซึมสามเหลี่ยม ASR ใดๆ ได้ดังนี้

แบ่งปริซึมสามเหลี่ยม ASR เป็นปริซึมสามเหลี่ยมมุมฉาก ASD และปริซึมสามเหลี่ยมมุมฉาก ARD โดยตัดตามแนวระนาบ ABCD ดังรูป
สร้างปริซึมสี่เหลี่ยมมุมฉาก PQRS ให้มีปริซึมสามเหลี่ยม ASR เป็นส่วนหนึ่ง ดังรูป

ปริมาตรของปริซึมสามเหลี่ยมมุมฉาก ASD เป็นครึ่งหนึ่งของปริมาตรของปริซึมสี่เหลี่ยมมุมฉาก ADSP และในทำนองเดียวกัน ปริมาตรของปริซึมสามเหลี่ยมมุมฉาก ARD ก็เป็นครึ่งหนึ่งของปริมาตรของปริซึมสี่เหลี่ยมมุมฉาก ADRQ

ดังนั้น ปริมาตรของปริซึมสามเหลี่ยมมุมฉาก ASR จึงเป็นครึ่งหนึ่งของปริมาตรของปริซึมสี่เหลี่ยมมุมฉาก PQRS นั่นคือ

ปริมาตรของปริซึมสามเหลี่ยม ASR	=	½ ของปริมาตรของปริซึมสี่เหลี่ยมมุมฉาก PQRS
	=	½ x (พื้นที่ของ □ PQRS x AB)
	=	(½ x พื้นที่ของ □ PQRS x AB)
	=	พื้นที่ฐานของปริซึมสามเหลี่ยม ASR x ความสูง
——————– นั่นคือ ปริมาตรของปริซึมสามเหลี่ยมใดๆ = พื้นที่ฐาน x ความสูง

เราสามารถนำสูตรการหาปริมาตรของปริซึมสามเหลี่ยมใดๆ ไปหาสูตรของปริซึมที่มีฐานรูปหลายเหลี่ยมได้โดยแบ่งฐานของปริซึมหลายเหลี่ยมออกเป็นรูปสามเหลี่ยมหลายๆ รูป ตัวอย่างเช่น เราแบ่งปริซึมห้าเหลี่ยม ซึ่งสูง h หน่วย ออกเป็นปริซึมสามเหลี่ยม 3 รูป ได้ดังนี้

ปริมาตรของปริซึมห้าเหลี่ยม	=	ปริมาตรของปริซึม 1 + ปริมาตรของปริซึม 2 + ปริมาตรของปริซึม 3
	=	(พื้นที่ฐานของปริซึม 1 x h ) + (พื้นที่ฐานของปริซึม 2 x h ) + (พื้นที่ฐานของปริซึม 3 x h )
	=	[พื้นที่ฐานของปริซึม 1 + พื้นที่ฐานของปริซึม 2 + พื้นที่ฐานของปริซึม 3] x h
	=	พื้นที่ฐานของปริซึมห้าเหลี่ยม x h