จำนวนและการดำเนินการ

จํานวนจริง ( Real number ) ประกอบด้วยจํานวนตรรกยะและจํานวนอตรรกยะ

  1. จํานวนตรรกยะ ( Rational number ) ประกอบด้วย จํานวนเต็ม ทศนิยมซ้ํา และเศษส่วน

        1. จํานวนเต็ม ซึ่งแบ่งเป็น 3 ชนิด คือ

            1.1 จํานวนเต็มบวก(I+)หรือจํานวนนับ (N)

                     ∴ I+  = N = {1, 2, 3, …}

            1.2 จํานวนเต็มศูนย์ มีจํานวนเดียว คือ {0}

            1.3 จํานวนเต็มลบ (I-)

                    ∴  I– = {-1, –2, –3, …}

            2. เศษส่วน เช่น 

            3. ทศนิยมซ้ํา เช่น 0.6, 0.12, 0.532  เป็นต้น

  2. จํานวนอตรรกยะ( irrational number ) คือ  จํานวนที่ไม่ใช่จํานวนตรรกยะ เขียนได้ในรูปทศนิยมไมซ้ํา เช่น

                   
                         π      มีค่าเท่ากับ     3.14159265…

        0.1010010001… มีค่าประมาณ    1.101

สมบัติของจำนวนเต็ม

กำหนดให้ a,b และc แทนจำนวนเต็มใดๆ

• สมบัติการสลับที่สำหรับการบวก    a + b = b + a
• สบบัติการสลับที่สำหรับการคูณ     a × b = b × a
• สมบัติการเปลี่ยนหมู่                    (a + b) + c = a + (b + c)                                                                                                                                   (a × b) × c = a × (b × c)
• สมบัติการแจกแจง                       a × (b + c) = (a × b) + (a × c)
• สมบัติของศูนย์                            a + 0 = 0 + a = a เรียกว่า เอกลักษณ์การบวก                                                                                                     a × 0 = 0 × a = 0                                                                                                                                        ถ้า a × b = 0 แล้ว a = 0 หรือ b = 0
• สมบัติของหนึ่ง                            1 × a = a × 1 เรียกว่า เอกลักษณ์การคูณ                                                                                                            a/1 = a

 สมบัติการบวก การลบ การคูณ การหาร

สมบัติของจํานวนจริง คือ การนําจํานวนจริงใด ๆ มากระทําต่อกันในลักษณะ เช่น  การบวก การลบ การคูณ การหาร หรือกระทําด้วยลักษณะพิเศษที่กําหนดขึ้น แล้วมีผลลัพธ์ที่เกิดขึ้นในลักษณะหรือทํานองเดียวกัน สมบัติที่ใช้ในการบวก การลบ การคูณ และการหาร มีดังนี้

2.1 สมบัติการเท่ากันของจํานวนจริง  กําหนด a, b, c เป็นจํานวนจริงใดๆ

2.2 สมบัติการบวกและการคูณในระบบจํานวนจริง  เมื่อกําหนดให้ a,b และ c เป็นจํานวนจริงใดๆ

    2.2.1 สมบัติการบวก

2.2.2 สมบัติการคูณ

    จากสมบัติของจํานวนจริงสามารถใช่พิสูจน์ทฤษฎีบทต่อไปนี้ได้
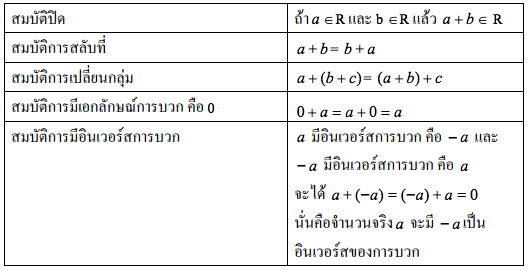
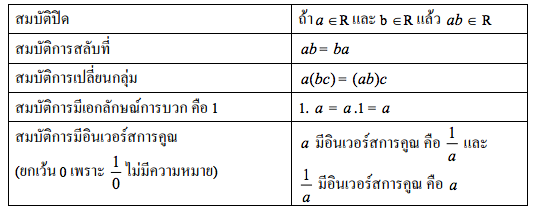
ทฤษฎีบทที่ 1 กฎการตัดออกสําหรับการบวก
เมื่อ a, b, c เป็นจํานวนจริงใดๆ

                ถ้า a + c = b + c แล้ว a = b
ถ้า a + b = a + c แล้ว b = c

ทฤษฎีบทที่ 2 กฎการตัดออกสําหรับการคูณ
เมื่อ a, b, c เป็นจํานวนจริงใดๆ
ถ้า ac = bc และ c ≠0 แล้ว a = b
ถ้า ab = ac และ a ≠0 แล้ว b = c

ทฤษฎีบทที่ 3 เมื่อ a เป็นจํานวนจริงใดๆ
a · 0 = 0
0 · a = 0

ทฤษฎีบทที่ 4 เมื่อ a เป็นจํานวนจริงใดๆ
(-1)a = -a
a(-1) = -a

ทฤษฎีบทที่ 5 เมื่อ a, b เป็นจํานวนจริงใดๆ
ถ้า ab = 0 แล้ว a = 0 หรือ b = 0

ทฤษฎีบทที่ 6 เมื่อ a เป็นจํานวนจริงใดๆ
a(-b) = -ab
(-a)b = -ab
(-a)(-b) = ab

การลบและการหารจํานวนจริง

        • การลบจำนวนจริง

                บทนิยาม     เมื่อ a, b เป็นจํานวนจริงใดๆ

                                       a -b = a + (-b)

                นั่นคือ a -b คือ ผลบวกของ a กับอินเวอร์สการบวกของ b

        • การหารจํานวนจริง
บทนิยาม     เมื่อ a, b เป็นจํานวนจริงใดๆ เมื่อ b ≠0
a/b = a( b^-1 )

                นั่นคือ a/b คือ ผลคูณของ a กับอินเวอร์สการคูณของ b

การเท่ากันของจำนวนจริง

การเท่ากันของจำนวน เราใช้ “ = ” แทนการเท่ากัน เช่น

1 + 2 = 3 ; 6 x 2 = 12

5 – 3 = 2 ; 24 ÷ 3 = 8

การเท่ากันในระบบจำนวนจริงมีสมบัติพื้นฐาน ดังนี้

1. สมบัติการสะท้อน

ถ้า a เป็นจำนวนจริงใด ๆ แล้ว a = a

เช่น 3 = 3

2. สมบัติการสมมาตร

เมื่อ a และ b เป็นจำนวนจริงใด ๆ ถ้า a = b แล้ว b = a

เช่น ถ้า 3 + 4 = 7 แล้ว 7 = 3 + 4

3. สมบัติการถ่ายทอด

เมื่อ a , b , c เป็นจำนวนจริงใด ๆ ถ้า a = b และ b = c แล้ว a = c

เช่น ถ้า 15 = 5 x 3 และ 5 x 3 = 10 + 5 แล้ว 15 = 10 + 5

4. สมบัติการบวกด้วยจำนวนที่เท่ากัน

เมื่อ a , b , c เป็นจำนวนจริงใด ๆ ถ้า a = b แล้ว a + c = b + c

เช่น ถ้า 9 + 1 = 10 แล้ว ( 9 + 1 ) + 2 = 10 + 2

5. สมบัติการคูณด้วยจำนวนที่เท่ากัน

เมื่อ a , b , c เป็นจำนวนจริงใด ๆ ถ้า a = b แล้ว ac = bc

เช่น ถ้า 18 = 9 x 2 แล้ว 18 x 3 = ( 9 x 2 ) x 3

สมบัติการไม่เท่ากันของจำนวนจริง

สมบัติเกี่ยวกับการไม่เท่ากันของจำนวนจริง มีดังนี้ ( ให้ a , b , c , d ∈ R )

การไม่เท่ากันของจำนวนจริง ไม่มีสมบัติการสะท้อน ไม่มีสมบัติการสมมาตร แต่มีสมบัติอื่นดังนี้

1. สมบัติการถ่ายทอด ถ้า a > b และ b > c แล้ว a > c

2. สมบัติการบวกด้วยจำนวนที่เท่ากัน ถ้า a > b แล้ว a + c > b + c

3. สมบัติการคูณจำนวนที่เท่ากัน ถ้า a > b และ c > 0 แล้ว ac > bc ถ้า a > b และ c < 0 แล้ว ac < bc

4. สมบัติการตัดออกสำหรับการบวก ถ้า a + c > b + c แล้ว a > b

5. สมบัติการตัดออกสำหรับการคูณ ถ้า ac > bc และ c > 0 แล้ว a > b ถ้า ac > bc และ c < 0 แล้ว a < b

ค่าสัมบูรณ์

ค่าสัมบูรณ์ของจำนวนจริงใดๆ คือ ค่าของตัวเลขที่ไม่มีเครื่องหมาย (บวก หรือ ลบ) มาเกี่ยวข้อง  ดังนั้น ค่าสัมบูรณ์จะเป็นบวกเสมอ “│  │” เป็นสัญลักษณ์ที่ใช้แทนค่าสัมบูรณ์ ค่าสัมบูรณ์ของ -5 และ +5

|-5| = |+5|= 5

การใช้แนวคิดนี้ในการแก้โจทย์ปัญหาต่อไปนี้

ตัวอย่างที่ 1

จงหาค่าของ |-7| และ |7|

│-7 │= 7

│ 7 │= 7

ตัวอย่างที่ 2

จงหาค่าของ |-150| และ |150|

│-150 │= 150

│150 │= 150

ตัวอย่างที่ 3

จงหาค่าของ

│5 -7 │= ?

=│-2│

= 2 เพราะค่าสัมบูรณ์ คือ จำนวนที่มีระยะห่างจากเลขศูนย์เท่ากันบนเส้นจำนวน