รูปเรขาคณิต (ความยาวด้านของสามเหลี่ยม จุดภายนอกและจุดภายใน)
รูปเรขาคณิต (Geometric figure) เป็นรูปที่ประกอบด้วย จุด เส้นตรง เส้นโค้ง ระนาบ ฯลฯ ตัวอย่างของรูปเรขาคณิต ได้แก่ รูปสามเหลี่ยม รูปสี่เหลี่ยม รูปวงกลม ทรงสี่เหลี่ยม ทรงกระบอก พีระมิด ทรงกลม ฯ
รูปสามเหลี่ยม (Triangle) เป็นรูปปิดที่ประกอบด้วยด้านสามด้าน
ความยาวรอบรูปของรูปสามเหลี่ยม (perimeter) คือ ผลบวกของความยาวของด้านทุกด้านของรูปสามเหลี่ยม
การจะสร้างรูปสามเหลี่ยมใด ๆ ความยาวของด้านทั้งสามจะต้องสัมพันธ์กัน โดยผลบวกของด้านที่สั้นสองด้าน จะต้องมีค่ามากกว่าด้านยาวที่สุด
จุดข้างในและจุดข้างนอก (Interior & Exterior point)
รูปเรขาคณิตที่เกิดจากเส้นโค้ง นอกจากวงกลม วงรี แล้วเราสามารถสร้างรูปจากเส้นโค้งได้มากมาย
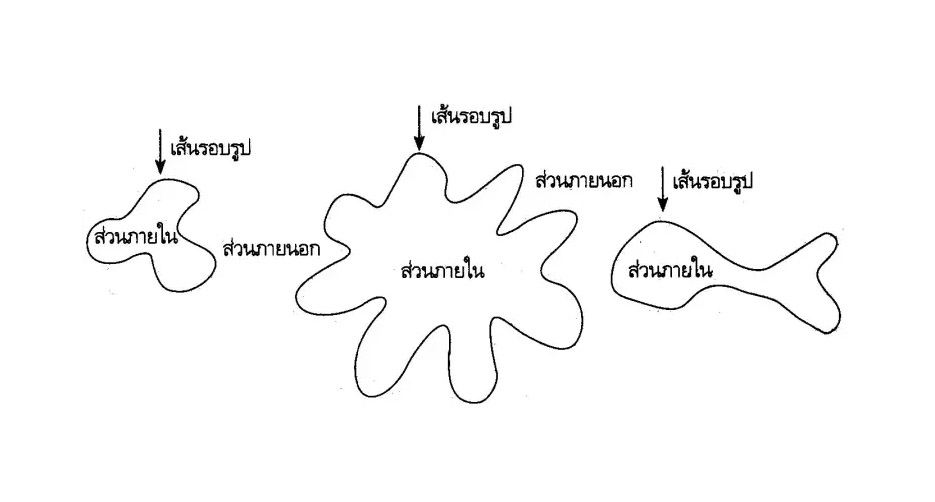
…….จากรูปข้างบน เราเรียกว่า รูปเส้นโค้งปิดเชิงเดียว (single closed curve) จะเป็นรูปเส้นโค้งปิดที่เส้นรอบรูปไม่ตัดกัน
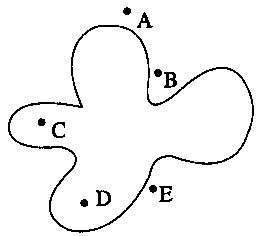
……. เส้นโค้งปิดเชิงเดียว จะมีเส้นรอบรูปเป็นเส้นแข่งเขตระหว่างส่วนที่อยู่ข้างในกับส่วนที่อยู่ข้างนอก โดยจะเรียกจุดที่อยู่ข้างในว่า จุดข้างใน (Interior point) และจุดที่อยู่ข้างนอกรูปปิดว่า จุดข้างนอก (Exterior point)
…….. จากรูป A, B, E เป็นจุดข้างนอก และ C, D เป็นจุดข้างใน
…….. ถ้าในกรณีที่เป็นรูปซับซ้อน เราอาจจะบอกไม่ได้ในทันทีว่าจุดใดเป็นจุดข้างในหรือจุดข้างนอก หรือถ้าหาก็อาจต้องเสียเวลาค่อนข้างมาก แต่ถ้าเราใช้ทฤษฎีของ ฌอร์ดอง (Jordan’s Theorem) ในการหาจุดข้างในและจุดข้างนอกอาจจะช่วยให้เร็วขึ้น
…….. ทฤษฎีของฌอร์ดอง กล่าวว่า ถ้าลากส่วนของเส้นตรงเส้นหนึ่งจากจุดนั้นออกมาข้างนอกรูปทางใดทางหนึ่ง แล้วส่วนของเส้นตรงนั้นตัดเส้นรอบรูปได้จำนวนจุดตัดเป็น จำนวนคี่ จุดนั้นจะเป็น จุดข้างใน แต่ถ้าได้จำนวนจุดตัดเป็น จำนวนคู่ จุดนั้นจะเป็น จุดข้างนอก

……. ลองทดสอบตัวเองดูสิครับว่า จุดใดเป็นจุดภายในและจุดใดเป็นจุดภายนอก