สรุปตรรกศาสตร์เบื้องต้น

ความหมายของศัพท์ตรรกศาสตร์
คำว่า “ตรรกศาสตร์” ได้มาจากศัพท์ภาษาสันสฤตสองศัพท์คือตรฺรกและศาสตฺรตรรก หมายถึงการตรึกตรอง ความคิด ความนึกคิด และคำว่าศาสตฺร หมายถึง วิชาตำรารวมกันเข้าเป็น“ตรรกศาสตร์” หมายถึงวิชาว่าด้วยความนึกคิดอย่างเป็นระบบปราชญ์ทั่วไปจึงมีความเห็นร่วมกันว่า ตรรกศาสตร์ คือวิชาว่าด้วย การใช้กฎเกณฑ์ การใช้เหตุผล
วิชาตรรกศาสตร์นั้นมีนักปราชญ์ทางตรรกศาสตร์ได้นิยามความหมายไว้มากมายนักปราชญ์เหล่านั้นคือ
1.พจนานุกรมศัพท์ปรัชญาอังกฤษ – ไทยฉบับราชบัณฑิตยสถาน นิยามความหมายว่า “ตรรกศาสตร์คือปรัชญาสาขาที่ว่าด้วยการวิเคราะห์และตัดสินความสมเหตุสมผลในการอ้างเหตุผล”
2.กีรติบุญเจือนิยามความหมายว่า“ตรรกวิทยาคือวิชาที่ว่าด้วยกฎเกณฑ์การใช้เหตุผล”
3.”WilfridHodges” นิยามความหมายว่า “ตรรกศาสตร์ คือการศึกษาระบบข้อเท็จจริงให้ตรงกับความเชื่อ”

ประพจน์ (Proposition)
ประพจน์ คือ ประโยคที่เป็นจริงหรือเป็นเท็จเพียงอย่างเดียวเท่านั้น
ประโยคเหล่านี้อาจจะอยู่ในรูปประโยคบอกเล่าหรือประโยคปฏิเสธก็ได้

ประโยคต่อไปนี้เป็นประพจน์
จังหวัดชลบุรีอยู่ทางภาคตะวันออกของไทย( จริง )
5 × 2 = 2 + 5 ( เท็จ )

ตัวอย่างต่อไปนี้ไม่เป็นประพจน์
โธ่คุณ( อุทาน )
กรุณาปิดประตูด้วยครับ( ขอร้อง )

ท่านเรียนวิชาตรรกวิทยาเพื่ออะไร( คำถาม )

ประโยคเปิด (Open sentence)
บทนิยาม ประโยคเปิดคือ ประโยคบอกเล่า ซึ่งประกอบด้วยตัวแปรหนึ่งหรือมากกว่าโดยไม่เป็นประพจน์ แต่จะเป็นประพจน์ได้เมื่อแทนตัวแปรด้วยสมาชิกเอกภพสัมพัทธ์ตามที่กำหนดให้ นั่นคือเมื่อแทนตัวแปรแล้วจะสามารถบอกค่าความจริง

      ประโยคเปิด เช่น
1.เขาเป็นนักบาสเกตบอลทีมชาติไทย
2. x + 5 =15
3. y < – 6
ประโยคที่ไม่ใช่ประโยคเปิด เช่น
1.10 เป็นคำตอบของสมการ X-1=7
2.โลกหมุนรอบตัวเอง
3.จงหาค่า X จากสมการ 2x+1=8

ตัวเชื่อม (connective)
1. ตัวเชื่อมประพจน์ ” และ ” ( conjunetion ) ใช้สัญลักษณ์แทน Ùและเขียนแทนด้วย P Ù Q แต่ละประพจน์มีค่าความจริง(truth value) ได้ 2 อย่างเท่านั้น คือจริง(True)หรือ เท็จ(False) ถ้าทั้ง P และ Qเป็นจริงจะได้ว่า PÙQ เป็นจริง กรณีอื่นๆP Ù Q เป็นเท็จเราให้นิยามค่าความจริง P Ù Q
โดยตารางแสดงค่าความจริง (truthtable) ดั้งนี้

P	Q	P Ù Q
T T F F	T F T F	T F F F

ตัวอย่าง 5+1 = 6 Ù 2 น้อยกว่า3 (จริง)

5+1 = 6 Ù 2 มากกว่า3 (เท็จ)
5+1 = 1 Ù2 น้อยกว่า 3 (เท็จ)
5+1 = 1 Ù 2 มากกว่า 3 (เท็จ)

2. ตัวเชื่อมประพจน์” หรือ ” ( Disjunction ) ใช้สัญลักษณ์แทน V และเขียนแทนด้วย P V Q และเมื่อ P V Q

จะเป็นเท็จ ในกรณีที่ทั้ง P และ Qเป็นเท็จเท่านั้น กรณีอื่น P V Q เป็นจริง เรา

ให้นิยามค่าความจริงของP V Q

ตัวอย่างตารางค่าความจริง ดังนี้

P	Q	P V Q
T T F F	T F T F	T T T F

ตัวอย่าง5 + 1= 6 V 2 น้อยกว่า 3(จริง)

5 + 1= 6 V 2 มากกว่า 3(จริง)
5 + 1= 1V 2 น้อยกว่า 3(จริง)
5 + 1= 1V 2 มากกว่า 3(เท็จ)

3. ตัวเชื่อมประพจน์“ ถ้า….แล้ว” Conditional)ใช้สัญลักษณ์แทน ®และเขียนแทนด้วย P®Q

นิยามค่าความจริงของP®Qโดยแสดงตารางค่าความจริงดังนี้

P	Q	P®Q
T T F F	T F T F	T F T T

ตัวอย่าง 1 < 2®2 < 3(จริง)
1 < 2®3 < 2(เท็จ)
2 < 1 ® 2 < 3(จริง)
2 < 1 ® 3 < 2(จริง)

4. ตัวเชื่อมประพจน์“ก็ต่อเมื่อ”(Biconditional)ใช้สัญลักษณ์แทน «และเขียนแทนด้วย P«Q

นั้นคือ P«Q จะเป็นจริงก็ต่อเมือ ทั้ง P และ Q เป็นจริงพร้อมกันหรือทั้ง P และ Q เป็นเท็จพร้อมกันตารางแสดงค่าความจริงของ P«Q

P	Q	P«Q
T T F F	T F T F	T F F T

ตัวอย่าง 1 < 2«2 < 3(จริง)
1 < 2«3 < 2(เท็จ)
2 < 1 « 2 < 3(จริง)
2 < 1 « 3 < 2(เท็จ)

5. นิเสธ (Negation)ใช้สัญลักษณ์แทน~ เขียนแทนนิเสธของ P ด้วย ~P ถ้า P เป็นประพจน์นิเสธของประพจน์ P คือประพจน์ที่มีค่าความจริงตรงข้ามกัน P

ตารางแสดงค่าความจริงดั้งนี้

P	~P
T F	F T

ตัวอย่าง ถ้า p แทนประโยคว่า “วันนี้เป็นวัน เสาร์” นิเสธของ p หรือ ~p คือประโยคที่ว่า “วันนี้ไม่เป็นวันเสาร์”

สัจนิรันดร์ (Tautology) และความขัดแย้ง (Contradiction)

1. สัจนิรันดร์(Tautology) คือ รูปแบบประพจน์ที่มีค่าความจริงเป็นจริงเสมอโดยไม่ขึ้นอยู่กับค่าความจริงของตัวแปรของแต่ละประพจน์ที่มีรูปแบบเป็นสัจนิรันดร์ เรียกว่า ประพจน์สัจนิรันดร์ (Tautology statement)ตัวอย่างที่ 1 P® PvQเป็นสัจนิรันดร์ เราสามารถพิสูจน์ได้หลายวิธี

P	Q	PvQ	P® PvQ
T T F F	T T T F	T T T F	T T T T

จากตารางแสดงค่าความจริงไม่ว่า P และ Q จะเป็นจริงหรือเท็จก็ตาม ประพจน์ P® PvQ เป็นจริงเสมอ ดังนั้นประพจน์นี้เป็น สัจนิรันดร์
2.ความขัดแย้ง (Contradiction) คือ รูปแบบประพจน์ที่มีค่าความจริงเป็นเท็จเสมอโดยไม่ขึ้นอยู่กับค่าความจริงของตัวแปรของแต่ละประพจน์ย่อยประพจน์ที่มีรูปแบบ เป็นความขัดแย้ง เรียกว่า ประพจน์ความขัดแย้ง (Contradicithonstatement)

ตัวอย่าง P^ ~Pเป็น ความขัดแย้ง ตารางแสดงค่าความจริง

p	~P	P^ ~P
T F	F T	F F

    

P ^ ~P มีค่าเป็นเท็จ สำหรับทุกๆ ค่าความจริงของ P
ดังนั้น P ^ ~P จึงเป็นความขัดแย้ง (Contradicithon )

ทฤษฎีตรรกสมมูล (Logical Equivalences)

ความรู้ประพจน์ตรรกะสมมูล (Logical equivalent statement)มีประโยชน์มากสำหรับการหาข้อโต้แย้งและข้อสรุปในทางคณิตศาสตร์ ซึ่งในทางปฏิบัติแล้ว การสรุปเหตุผลในแต่ละรูปจะยุ่งยากมากหากไม่อาศัยทฤษฎี ตรรกะสมมูลใน การกล่าวอ้าง ดังนั้นจึงสรุปทฤษฎีตรรกะสมมูลไว้สำหรับใช้อ้างอิงต่อไป
กำหนดให้ p , q , r แทนประพจน์ใดๆ t แทนสัจนิรันดร์ c แทนความขัดแย้ง

1. กฎการสลับที่ (Commutative laws)
   p ^ q = q ^p , p ^ q = q v p

   2.กฎการเปลี่ยนหมู่ (Associative laws)
   (p ^ q) ^r = p ^ (q ^ r) , (p ^ q) v r = p v (q ^ r)

   3. กฎการแจกแจง (Distributive laws)
   p ^ (q v r) = (p ^ q) v ( p ^ r) , p v (q ^ r) = (p v q) ^ ( p v r)

   4. กฎเอกลักษณ์ (Identity laws)
   p v t = t , p ^ t = p

   5. กฎนิเสธ (Negative laws)
   p v ~p = t , p ^ ~ p = c

   6.กฎนิเสธซ้อนนิเสธ (Double negative laws)
   ~(~p) = p

   7. กฎนิจพล (Idempotent laws)
   p ^p = p , p = p

   8. กฎของเดอมอเกน (demerger’s laws)
   ~(p ^q) = ~p v ~q , ~(p v q) = ~p v ~q

   9. กฎการจำกัดขอบข่าย (Universal bound laws)
   p v t = t , p ^ c = c

   10. กฎการซึมซับ (Absorption laws)
   p v (p ^ q) = p , p ^ (p v q) = p

   11. นิเสธของ c และ t
   ~t = c , ~c=t

ตัวบ่งปริมาณ(Quantified statement)

ตัวบ่งปริมาณในตรรกศาสตร์ มี 2 ชนิด คือ

1)ตัวบ่งปริมาณ “ทั้งหมด” หมายถึงทุกสิ่งทุกอย่างที่ต้องการพิจารณาในการ

นำไปใช้อาจใช้คำอื่นที่มีความหมายเช่นเดียวกับ “ทั้งหมด” ได้ได้แก่”ทุก”

“ทุก ๆ””แต่ละ””ใด ๆ”ฯลฯเช่น คนทุกคนต้องตาย, คนทุก ๆ คนต้องตาย,

คนแต่ละคนต้องตาย, ใคร ๆ ก็ต้องตาย

2)ตัวบ่งปริมาณ “บาง” หมายถึงบางส่วนหรือบางสิ่งบางอย่างที่ต้องการ

พิจารณา ในการนำไปใช้อาจใช้คำอื่นที่มีความหมายเช่นเดียวกันได้ ได้แก่

“บางอย่าง””มีอย่างน้อยหนึ่ง” เช่น สัตว์มีกระดูกสันหลังบางชนิดออกลูกเป็น

ไข่, มีสัตว์มีกระดูกสันหลังอย่างน้อยหนึ่งชนิดที่ออกลูกเป็นไข่

ค่าความจริงของประพจน์ที่มีตัวบ่งปริมาณ

1.∀x[P(x)] มีค่าความจริงเป็นจริง เมื่อ x ทุกตัวในเอกภพสัมพัทธ์ทำให้ P(x) เป็นจริง
2. ∀x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อมี x อย่างน้อย 1 ตัวที่ทำให้ P(x) เป็นเท็จ
3. ∃x[P(x)] มีค่าความจริงเป็นจริง เมื่อมี x อย่าน้อย 1 ตัวที่ทำให้ P(x) เป็นจริง
4.∃x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อไม่มี x ใดๆ ในเอกภพสัมพัทธ์ที่ทำให้ P(x) เป็นจริง

การให้เหตุผล (Reasoning)โดยทั่วไปกระบวนการให้เหตุผลมี 2 ลักษณะคือ 1.การให้เหตุผลแบบนิรนัยเป็นการให้เหตุโดยนำข้อความที่กำหนดให้ซึ่งต้องยอมรับว่าเป็นจริง ทั้งหมด เรียกว่า เหตุ และข้อความจริงใหม่ที่ได้เรียกว่า ผลสรุป ซึ่งถ้า พบว่าเหตุที่กำหนดนั้นบังคับให้เกิดผลสรุปไม่ได้ แสดงว่า การให้เหตุผลดังกล่าวสมเหตุสมผล แต่ถ้าพบว่าเหตุที่กำหนดนั้นบังคับให้เกิดผลสรุปไม่ได้แสดงว่า การให้เหตุผลดังกล่าวไม่สมเหตุสมผล

ตัวอย่างเหตุ 1.คนทุกคนต้องหายใจ

2 . นายเด่นต้องหายใจ

ผลสรุปนายเด่นต้องหายใจ

จะเห็นว่า จากเหตุที่1 และเหตุที่ 2 บังคับให้เกิดผลสรุปดังนั้นการให้เหตุผลนี้สมเหตุสมผลสมเหตุสมผล

2.การให้เหตุผลแบบอุปนัย เป็นการให้เหตุผลโดยอาศัยข้อสังเกตหรือผลการทดลองจากหลายๆตัวอย่าง มาสรุปเป็นข้อตกลง หรือข้อคาดเดาทั่วไป หรือ คำพยากรณ์และจะต้องมีข้อสังเกต หรือ ผลการทดลอง หรือ มีประสบการณ์ที่มากพอที่จะปักใจเชื่อได้ แต่ก็ยังไม่สามารถแน่ใจในผลสรุปได้เต็มที่เหมือนกับการให้เหตุผลแบบนิรนัย

ตัวอย่างการให้เหตุผลแบบอุปนัย เช่น เราเคยเห็นว่ามีปลาจำนวนมากที่ออกลูกเป็นไข่เราจึงอนุมานว่า“ปลาทุกชนิดออกลูกเป็นไข่ ”ซึ่งกรณีนี้ถือว่าไม่สมเหตุสมผลทั้งนี้เพราะข้องสังเกตหรือ ตัวอย่างที่พบว่ายังไม่มากพอที่จะสรุปเพราะโดยข้อเท็จจริงแล้วมีปลาบางชนิดที่ออกลูกเป็นตัว เช่นปลาหางนกยูง เป็นต้น
ตัวอย่างความสมเหตุสมผลของการให้เหตุผลโดย

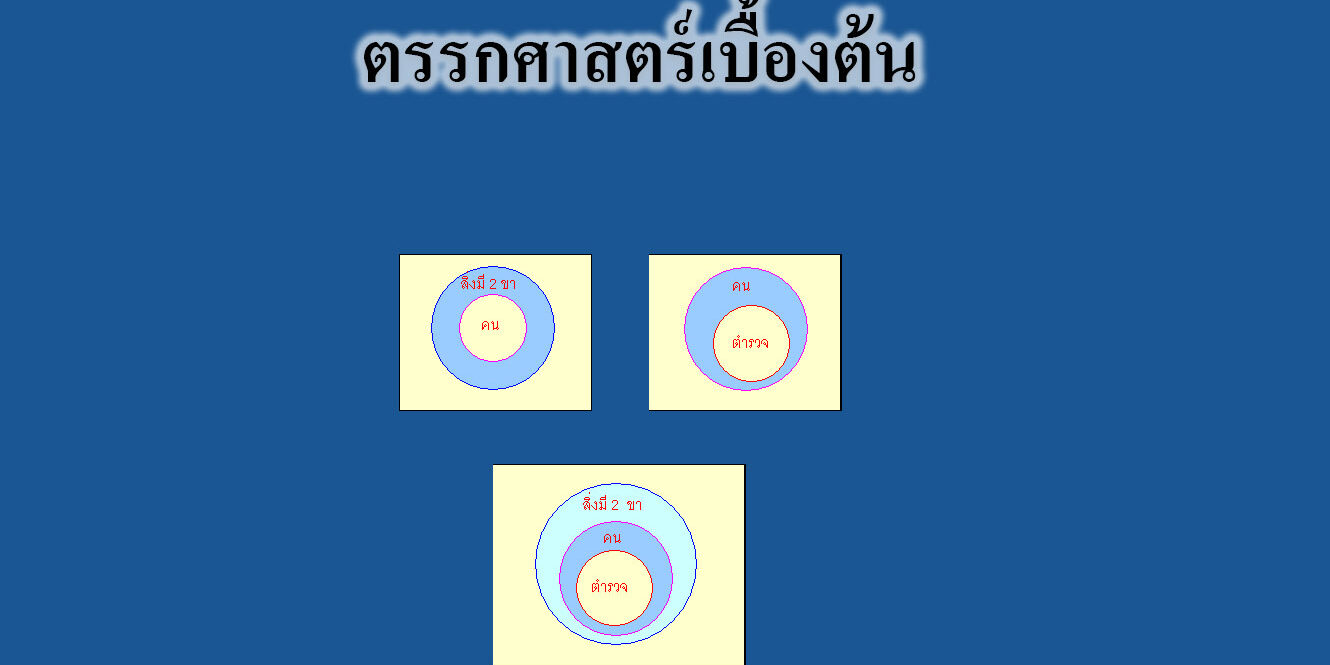
ตัวอย่างที่ 1 เหตุ 1 : คนทุกคนเป็นสิ่งที่มีสองขา

เหตุ 2 : ตำรวจทุกคนเป็นคน

ผลสรุป ตำรวจทุกคนเป็นสิ่งที่มีสองขา
จากเหตุ 1

จากเหตุ 2

แผนภาพรวม

จากแผนภาพจะเห็นว่า วงของ ” ตำรวจ ” อยู่ในวงของ ” สิ่งมี 2 ขาแสดง ” แสดงว่า ” ตำรวจทุกคนเป็นคนมีสองขา ” ซึ่งสอดคล้องกับผลสรุปที่กำหนดให้ ดังนั้น การให้เหตุผลนี้สมเหตุสมผล

การใช้ความสัมพันธ์ระหว่างพจน์ ในการตรวจสอบความสมเหตุสมผล

ตัวอย่างที่ 1 เหตุ จำนวนตรรกยะทุกจำนวนเป็นจำนวนจริง1 เป็นจำนวนอตรรยะ  ผล 1 เป็นจำนวนจริง
พจน์กลาง คือ จำนวนอตรรกยะ กระจายในข้อตั้งแรก ตรรกบทดังกล่าวจึงสมเหตุสมผล

ตัวอย่างที่ 2 เหตุ คนไทยทุกคนเป็นผู้ที่ยิ้มแย้มแจ่มใส ชาวปากเซเป็นคนยิ้มแย้มแจ่มใส ผลชาวปากเซเป็นคนไทย
พจน์กลาง คือ คนยิ้มแย้มแจ่มใส เป็นพจน์ไม่กระจาย ตรรกบทดังกล่าวจึง ไม่สมเหตุสมผล