การโปรแกรมเชิงเส้น (Linear Programming)

โปรแกรมเชิงเส้น (Linear Programming) เป็นเทคนิคที่รู้จักกันแพร่หลายและเป็นส่วนหนึ่งของการวิจัยดำเนินงาน (Operations Research) ในหลายๆด้าน นักบริหาร วิศวกรหรือนักวิทยาศาสตร์ในหลายๆ หน่วยงานได้ประยุกต์ใช้วิธีการทางโปรแกรมเชิงเส้น ในการแก้ปัญหาทางการจัดสรรปัจจัยหรือทรัพยากร (allocating resource) โดยที่ปัจจัยหรือทรัพยากรมีความหมายรวมถึงวัตถุดิบ กำลังคน เวลา สถานที่ เงินตรา หรือความรู้ความสามารถต่างๆ ปัญหาการจัดสรรปัจจัยและทรัพยากรเกิดขึ้นเมื่อเราต้องการจัดสรรทรัพยากรที่มีอยู่จำกัดทั้งขนาด ปริมาณ และขอบเขตของการใช้งาน เพื่อให้เกิดประโยชน์สูงสุด

โปรแกรมเชิงเส้นเป็นเทคนิคในการแก้ไขปัญหาทางการจัดสรรปัจจัยและทรัพยากรที่มีลักษณะความสัมพันธ์ของตัวแปรต่างๆ เป็นแบบเชิงเส้น โดยมีจุดหมายเพื่อแก้ปัญหาและตัดสินใจให้เกิดผลตามแนวทางการดำเนินงานที่ดีที่สุด (optimal) เช่นกำไรสูงสุด ค่าใช้จ่ายน้อยที่สุด หรือแนวทางการตำเนินงานอื่นๆ ที่ให้ผลประโยชน์มากที่สุดต่อระบบนั้นๆ โดยพิจารณาเงื่อนไขหรือข้อจำกัดที่กำหนด เช่นสภาวะตลาด การขาดแคลนวัตถุดิบ กำลังคน เงินทุน สถานที่ ความรู้ข้อกำหนดของกฎหมายและระเบียบต่างๆของสังคม นโยบายของฝ่ายบริหาร ขอบข่ายของธุรกิจที่ดำเนินอยู่และอื่นๆ ตัวอย่างเช่น การใช้เทคนิคทางโปรแกรมเชิงเส้นที่ใช้กับการแก้ปัญหาทางด้านขนส่งสินค้า ซึ่งจะเกี่ยวข้องกับสินค้าชนิดต่างๆ น้ำหนักและขนาดของสินค้า ราคาขนส่งสินค้า กำลังคนที่ใช้ในการขับรถ โดยมีข้อจำกัดต่างๆ เช่น ปริมาณและขนาดของรถที่มีอยู่ น้ำหนักของสินค้าที่สามารถบรรทุกได้ต่อเที่ยว ปริมาณความต้องการของตลาด เงินทุนจำกัด เวลาที่ในการขนส่งสินค้า นอกจากนี้โปรแกรมเชิงเส้นได้ถูกนำไปใช้ในการแก้ปัญหาทางด้านการผลิตของอุตสาหกรรมต่างๆ ซึ่งจะต้องเกี่ยวข้องโดยตรงกับวัตถุดิบชนิดต่างๆ ที่ใช้ในการผลิต ชนิดของเครื่องจักรที่มี กำลังคนที่ผลิต ราคาขาย และการตลาด โดยมีเงื่อนไขต่างๆ เช่น ขนาดขีดความสามารถในการผลิตของเครื่องจักรและแรงงาน ปริมาณความต้องการของตลาด ปริมาณวัตถุดิบและพลังงานอื่นๆในการผลิตเช่น น้ำ น้ำมัน ไฟฟ้า ไม้ มีอยู่ในจำนวนจำกัด เงินทุนจำกัด

เทคนิคทางการโปรแกรมเชิงเส้น ในการวิจัยดำเนินงานนี้พัฒนามาจากผลความก้าวหน้าทางวิทยาศาสตร์ ซึ่งมีแนวคิดริเริ่มมาจากนักคณิตศาสตร์วิทยาศาสตร์หลายๆท่านซึ่งได้นำไปใช้ในทฤษฎีเกม รวมทั้งถูกพัฒนานำไปใช้ในทางการขนส่ง นอกจากนี้ได้มีการใช้เทคนิคดังกล่าวในการแก้ปัญหาทางโภชนาการ ต่อมาได้มีการใช้คณิตศาสตร์และเทคนิคที่เกี่ยวข้องมาแก้ปัญหาทางการวางแผนโครงงานในกองทัพ

ปัจจุบันเป็นที่ยอมรับกันในหลายๆวงการในการนำเทคนิคทางการโปรแกรมเชิงเส้นไปใช้ประโยชน์ในหลายๆด้านเช่น ทางการเกษตร ทางเศรษฐศาสตร์ และการจัดการเกี่ยวกับการผลิต ทางอุตสาหกรรม
รูปแบบแทนระบบทางคณิตศาสตร์ของโปรแกรมเชิงเส้น
โปรแกรมเชิงเส้นประกอบไปด้วย 2 ส่วน ดังนี้

1. มีสมการกำหนดเป้าหมาย (objective function) คือสมการแสดงความสัมพันธ์ของต้นทุน กำไร เพื่อให้กำหนดเป้าหมายสูงสุดหรือต่ำสุด

2. มีสมการแสดงขอบข่าย (constraints) ซึ่งแสดงข้อจำกัดต่างๆของปัจจัยหรือทรัพยากรในรูปสมการหรืออสมการ
โดยที่สมการต่างๆ ทั้งหมดเป็นสมการเชิงเส้น เมื่อเทียบกับตัวแปร

คำตอบของสมการแสดงขอบข่ายอาจจะมีได้หลายคำตอบ ซึ่งคำตอบเหล่านี้อยู่ภายใต้ข้อจำกัดต่างๆที่กำหนดให้ อย่างไรก็ตามสมการกำหนดเป้าหมายเป็นตัววัดผลหรือตัวตัดสินว่าระหว่างคำตอบทั้งหมดของสมการแสดงขอบข่าย คำตอบใดเป็นคำตอบที่ดีที่สุด นั่นคือคำตอบนั้นจะทำให้สมการกำหนดเป้าหมายมีค่าที่ดีที่สุด ซึ่งเราจะต้องพยายามหาค่าเป็นไปตามเป้าหมายโดยอาศัยเทคนิคที่มีอยู่ ตัวแปรต่างๆ จะเป็นตัวแทนจำนวนปริมาณหรือค่าของปัจจัยที่มีอยู่จำกัดโดยการกำหนดของสมการหรืออสมการในขอบข่ายของปัญหา

ตัวอย่างง่ายๆ ของโปรแกรมจะประกอบไปด้วยตัวแปรตัดสินใจซึ่งเป็นค่าอินพุท และเอาท์พุต ซึ่งเป็นผลลัพธ์ โดยที่ค่าของตัวแปรเหล่านี้อยู่ในข้อจำกัดของปัจจัยต่างๆที่กำหนด จุดประสงค์ของโปรแกรมเชิงเส้นก็คือหาค่าของตัวแปรเหล่านี้ที่ทำให้สมการกำหนดเป้าหมายมีค่าที่ดีที่สุด

ขั้นตอนการดำเนินการของโปรเกรมเชิงเส้น

ขั้นตอนของการใช้โปรแกรมเชิงเส้นในการแก้ปัญหา ประกอบไปด้วย

1. จัดรูปแบบแทนระบบของปัญหา (Model Formulation)
ก่อนอื่นต้องศึกษาข้อมูลองค์ประกอบของปัญหาให้เข้าใจ โดยเลือกเฉพาะองค์ประกอบที่สำคัญและมีอิทธิพลมาก แล้วจัดตั้งตัวแปรแทนส่วนประกอบของปัญหานั้นๆ ให้ถูกต้อง

2. การหาผลลัพธ์ของรูปแบบแทนระบบของปัญหา (Model Solution)

การจัดตั้งรูปแบบแทนระบบของปัญหา (Model Formulation)
ในการจัดตั้งรูปแบบแทนระบบของปัญหาโดยใช้โปรแกรมเชิงเส้น เราต้องทำความเข้าใจและศึกษาปัญหาอย่างชัดเจน นอกจากนี้ยังต้องสามารถระบุสิ่งต่อไปนี้ในปัญหา
1. ตัวแปรตัดสินใจ หรือเรียกสั้นๆ ว่า ตัวแปร (decision variables) ซึ่งคือตัวแปรที่สำหรับใส่เข้าไปในระบบ และเป็นตัวแปรที่เราสามารถจะควบคุมได้ ตัวแปรนี้เป็นสิ่งสำคัญที่เราจะป้อนเข้าไปในระบบเพื่อให้เกิดประโยชน์สูงสุด ตัวอย่างเช่น จำนวนสินค้าที่จะผลิตซึ่งเป็นตัวแปรที่เราควบคุมได้
2. พารามิเตอร์เป็นค่าในระบบที่เราไม่สามารถควบคุมได้ ตัวอย่างเช่นราคาสินค้าซึ่งขึ้นอยู่กับกลไกตลาด
3. สมการกำหนดเป้าหมาย (objective function) คือสมการแสดงความสัมพันธ์ของต้นทุน กำไร เพื่อให้กำหนดเป้าหมายสูงสุดหรือต่ำสุด
4. สมการแสดงขอบข่าย (constraints) ซึ่งแสดงข้อจำกัดต่างๆของปัจจัยหรือทรัพยากรในรูปสมการหรืออสมการ

โปรแกรมเชิงเส้นตรง (linear Programming)

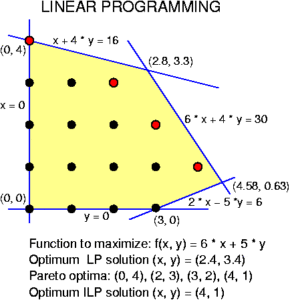
โปรแกรมเชิงเส้นตรง (linear Programming)
เป็นเทคนิคเชิงปริมาณอย่างหนึ่งที่เป็นที่นิยมนำไปใช้กันอย่างแพร่หลายในการดำเนินงานของธุรกิจปัจจุบัน
เป็นตัวแบบทางคณิตศาสตร์ที่สร้างขึ้นแทนปัญหาที่เกิดขึ้นภายในองค์กร เพื่อหาแนวทางในการแก้ปัญหาที่ดีที่สุดตามเป้าหมายที่ตั้งไว้ และสอดคล้องกับเงื่อนไขที่มีอยู่ในปัญหานั้นๆ โดยที่ความสัมพันธ์ของตัวแปรต่างๆ ในเป้าหมายและในเงื่อนไขของปัญหาจะอยู่ในรูปเส้นตรง

ลักษณะปัญหาที่ใช้การกำหนดโปรแกรมเชิงเส้นตรง
ส่วนใหญ่จะนำไปใช้เกี่ยวกับปัญหาด้านการจัดสรรทรัพยากรที่มีอยู่อย่างจำกัด เช่น วัตถุดิบ แรงงาน เงิน เวลา สถานที่ เป็นต้น
มีจุดมุ่งหมายที่จะจัดสรรทรัพยากรให้เกิดประโยชน์สูงสุด หรือเสียค่าใช้จ่ายต่ำสุด

ขอบคุณข้อมูล https://www.dek-d.com/