กราฟของฟังก์ชันกำลังสอง

1 แนะนำฟังก์ชัน

2 กราฟของฟังก์ชันกำลังสอง

ฟังก์ชันและกราฟของฟังก์ชัน

มโนทัศน์ของกราฟของฟังก์ชันสามารถวางนัยทั่วไปเป็นกราฟของความสัมพันธ์ (graph of a relation) สังเกตว่าถึงแม้ฟังก์ชันหนึ่ง ๆ สามารถระบุได้ด้วยกราฟของมันเสมอ แต่ฟังก์ชันสองฟังก์ชันที่มีโคโดเมนต่างกันก็อาจมีกราฟเหมือนกันได้ ฟังก์ชันเหล่านั้นจึงไม่ใช่ฟังก์ชันเดียวกัน ยกตัวอย่าง ฟังก์ชันพหุนามกำลังสามในตัวอย่างเป็นฟังก์ชันทั่วถึง (surjection) ถ้าโคโดเมนเป็นจำนวนจริง แต่จะไม่ใช่ฟังก์ชันทั่วถึงถ้าโคโดเมนเป็นจำนวนเชิงซ้อน

การทดสอบว่ากราฟเส้นโค้งหนึ่ง ๆ เป็นฟังก์ชันของ x หรือไม่ ให้ใช้การทดสอบเส้นแนวยืน (vertical line test) ในทางกลับกัน การทดสอบว่ากราฟเส้นโค้งหนึ่ง ๆ เป็นฟังก์ชันของ y หรือไม่ ให้ใช้การทดสอบเส้นแนวนอน (horizonal line test) ถ้าฟังก์ชันนั้นมีฟังก์ชันผกผัน กราฟของฟังก์ชันผกผันจะหาได้จากเงาสะท้อนในกระจกของกราฟของฟังก์ชันเดิม โดยมีเส้นตรงy = x เป็นแกน

ในทางวิทยาศาสตร์ วิศวกรรมศาสตร์ เทคโนโลยี การเงิน และอื่น ๆ กราฟถูกใช้เป็นเครื่องมืออเนกประสงค์ กรณีง่ายสุดคือตัวแปรหนึ่ง ๆ จะถูกลงจุด (plot) เป็นฟังก์ชันของตัวแปรอื่น โดยใช้แกนที่ตัดกันเป็นมุมฉากตามปกติ

ในรากฐานของคณิตศาสตร์สมัยใหม่อันเป็นที่รู้จักกันว่าทฤษฎีเซต ฟังก์ชันและกราฟของฟังก์ชันโดยพื้นฐานถือว่าคือสิ่งเดียวกัน

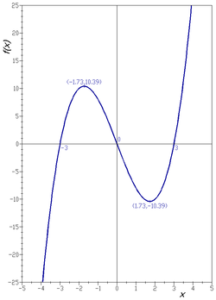
กราฟของฟังก์ชันf(x) = x³ − 9x

ฟังก์ชันกำลังสอง(Quadratic function)

ฟังก์ชันพีชคณิตที่มีตัวแปรต้นกำลังศูนย์หรือหนึ่งนั้นเป็นฟังก์ชันเชิงเส้น นอกเหนือจากนี้จะให้กราฟที่มีลักษณะเป็นเส้นโค้งในที่นี้เราจะศึกษาฟังก์ชันที่อยู่ในรูปของพหุนามกำลังสอง

ฟังก์ชันกำลังสองเป็นฟังก์ชันที่อยู่ในรูป    y   =   ax² + bx + c   เมื่อ  a, b, c  เป็นจำนวนจริงใด ๆ  และ  a ¹ 0   ซึ่งกราฟของฟังก์ชันกำลังสอง  เรียกว่า  พาราโบลา

1)     y  =  2x² + 3x – 10     เมื่อ   a = 2 ,  b = 3   และ  c = -1

2)     y  =   x² + 1                เมื่อ   a = 1 ,  b = 0   และ  c =  1

3)     y  =  -x² + 2x + 1       เมื่อ   a = -1 ,  b = 2   และ  c = 1

                1)   กราฟของฟังก์ชันกำลังสอง ที่กำหนดด้วยสมการ    y  =  ax²   เมื่อ  a ¹ 0

กราฟของฟังก์ชันกำลังสอง   มีชื่อเรียกว่า  พาราโบลา  ซึ่งลักษณะของกราฟของฟังก์ชันขึ้นอยู่กับค่าของ  a , b  และ  c   และเมื่อ  a  เป็นบวกหรือลบ  จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ  และกราฟของฟังก์ชันกำลังสองที่กำหนดด้วยสมการ    y  =  ax²   เมื่อ  a ¹ 0       เมื่อ  a  > 0   และชนิดคว่ำ   เมื่อ   a < 0

                สรุป                ลักษณะของกราฟที่กำหนดด้วยสมการ    y  =  ax²   เมื่อ  a ¹ 0

!  เมื่อ   a > 0  ได้พาราโบลาหงาย  จุดต่ำสุดอยู่ที่  (0, 0)

เมื่อ   a < 0   ได้พาราโบลาคว่ำ   จุดสูงสุดอยู่ที่  (0, 0)

!  แกนสมมาตรคือ  แกน  Y   หรือเส้นตรง   X  =  0 ,

สมการแกนสมมาตรคือ  X  =  0

!  เมื่อ   a > 0   ค่าต่ำสุดคือ  0  และ  เมื่อ  a < 0   ค่าสูงสุดคือ  0

!  | a |  ยิ่งมากกราฟยิ่งแคบ

2)  กราฟที่กำหนดด้วยสมการ   y  =  ax² + k   เมื่อ  a ¹ 0  และ k ¹ 0

กราฟที่กำหนดด้วยสมการ   y  =  ax² + k   เมื่อ  a ¹ 0  และ k ¹ 0  จะเป็นกราฟพาราโบลาที่มีจุดวกกลับหรือจุดสูงสุดหรือจุดต่ำสุด  อยู่ที่  (0, k)  และแกนสมมาตรคือ  แกน  Y

 กราฟฟังก์ชันกำลังสอง

พหุนามกำลังสองอยู่ในรูปของ ax² + bx + c เมื่อ a, b และ c เป็นจำนวนจริงใด ๆ เรานิยามเป็นฟังก์ชัน

P(x) = ax² + bx + c

= a[(x + b/(2a))² –  b²/(4a²) + c/a]

= a[(x + b/(2a))²  – (b² – 4ac)/(4a²)]

ถ้ากำหนดให้  h = – b/2a และ k = – (b² – 4ac)/(4a) ฟังก์ชันที่อยู่รูป

P(x) = a(x – h)² + k

มีกราฟเป็นรูปพาราโบลา

กรณีที่ a > 0 จะเป็นกราฟพาราโบลาหงายและมีต่ำสุดอยู่ที่จุด (h,k)

กรณีที่ a < 0 จะเป็นกราฟพาราโบลาคว่ำมีจุดสูงสุดอยู่ที่จุด (h,k)

สรุป        ลักษณะของกราฟที่กำหนดด้วยสมการ    y   =   ax² + k

ถ้า  a  >  0   ได้พาราโบลาหงาย   จุดต่ำสุดอยู่ที่  (0, k)  ค่าต่ำสุด  =  k

ถ้า  a  <  0   ได้พาราโบลาคว่ำ  จุดสูงสุดอยู่ที่  (0, k)   ค่าสูงสุด  =  k

แกนสมมาตรคือ  แกน  y  หรือเส้นตรง  x  =  0   สมการแกนสมมาตรคือ  x  =  0

ถ้า   k > 0   จุดวกกลับอยู่เหนือแกน  X

ถ้า   k < 0   จุดวกกลับอยู่ใต้แกน  X

ถ้า  a, k  มีเครื่องหมายเหมือนกัน  กราฟไม่ตัดแกน  X

ถ้า  a, k  มีเครื่องหมายต่างกัน  กราฟจะตัดแกน  X

                3.  กราฟของ   y  =  a(x – h)²     เมื่อ   a ¹ 0  และ h > 0 

                      3.1)  กราฟที่กำหนดด้วยสมการ    y   =   a(x – h)²    เมื่อ  a ¹ 0  และ  h  ¹ 0   จะเป็นกราฟ

พาราโบลาที่มีจุดวกกลับหรือจุดสูงสุดหรือจุดต่ำสุดอยู่ที่  (h, 0) และแกนสมมาตรคือเส้นตรง  x = h

3.2)  กราฟของ   y  =  a(x – h)²     เมื่อ   a ¹ 0  และ  h < 0 

ถ้า  h < 0   จะได้สมการใหม่เป็น     y        =    a(x – (-h))²

=    a(x + h)²

สรุป        ลักษณะของกราฟที่กำหนดด้วยสมการ    y   =   a(x – h)²

ถ้า  a  >  0   ได้พาราโบลาหงาย   จุดต่ำสุดอยู่ที่  (h, 0)  ค่าต่ำสุด  =  0

ถ้า  a  <  0   ได้พาราโบลาคว่ำ  จุดสูงสุดอยู่ที่  (h, 0)   ค่าสูงสุด  =  0

แกนสมมาตรคือ  เส้นตรง  x  =  h   สมการแกนสมมาตรคือ  x  =  h

h > 0   แกนสมมาตรอยู่ทางซ้ายของแกน  Y

h < 0   แกนสมมาตรอยู่ทางขวาของแกน  Y

                4.  กราฟของฟังก์ชันกำลังสองที่กำหนดด้วยสมการ  y  =  a(x – h)² + k  เมื่อ  a ¹ 0 ,  h ¹ 0
และ  k ¹ 0   จะเป็นพาราโบลาที่มีจุดวกกลับหรือจุดสูงสุดหรือจุดต่ำสุดอยู่ที่  (h, k)  และมีแกนสมมาตรคือ  เส้นตรง  x  =  h

สรุป        ลักษณะของกราฟที่กำหนดด้วยสมการ    y   =   a(x – h)² + k

เมื่อ  a  >  0   ได้พาราโบลาหงาย   จุดต่ำสุดอยู่ที่  (h, k)  ค่าต่ำสุด  =  k

เมื่อ  a  <  0   ได้พาราโบลาคว่ำ  จุดสูงสุดอยู่ที่  (h, k)   ค่าสูงสุด  =  k

ถ้า   k > 0   จุดวกกลับอยู่เหนือแกน  X

ถ้า   k < 0   จุดวกกลับอยู่ใต้แกน  X

แกนสมมาตร  คือ  เส้นตรง  x  =  h   สมการแกนสมมาตรคือ  x  =  h

ถ้า  h > 0   แกนสมมาตรอยู่ทางซ้ายมือของแกน  Y

ถ้า  h < 0   แกนสมมาตรอยู่ทางขวามือของแกน  Y

ถ้า  a  และ  k  มีเครื่องหมายเหมือนกันกราฟไม่ตัดแกน  X

ถ้า  a  และ  k  มีเครื่องหมายต่างกันกราฟตัดแกน  X