คณิตศาสตร์ม.2 เรื่องเส้นขนาน
เส้นตรงสองเส้นที่อยู่ระนาบเดียวกัน ขนานกันก็ต่อเมื่อเส้นตรงทั้งสองเส้นนั้นไม่ตัดกัน
ระยะห่างระหว่างเส้นขนานจะเท่ากันเสมอ
ถ้าเส้นตรงสองเส้นมีระยะห่างระหว่างเส้นตรงเท่ากันเสมอ เส้นตรงคู่นั้นจะนขานกัน
มุมภายใน มุมแย้งและมุมภายนอกเกิดจากเส้นตรงเส้นหนึ่งมาตัดเส้นตรงของเส้นขนานคู่นั้น เรียกว่า “เส้นตัดขวาง” หรือ “เส้นตัด”
เมื่อเส้นตรงเส้นหนึ่ง ตัดเส้นตรงคู่หนึ่ง เส้นตรงคู่นั้นจะขนานกันก็ต่อเมื่อ ขนาดของมุมภายในที่อยู่บนข้างเดียวกันของเส้นตัดรวมกันเท่าเท่ากับ 180 องศา
เมื่อเส้นตรงเส้นหนึ่งตัดเส้นตรงคู่หนึ่ง เส้นตรงคู่นั้นจะขนานกันก็ต่อเมื่อ มุมแย้งมีขนาดเท่ากัน
ถ้าเส้นตรงสองเส้นตัดกันแล้ว มุมตรงข้ามจะมีขนาดเท่ากัน
ถ้าเส้นตรงสองเส้นขนานกันและมีเส้นตัด แล้วมุมภายนอกและมุมภายในที่อยู่ตรงข้ามบนข้างเดียวกันของเส้นตัดมีขนาดเท่ากัน
เมื่อเส้นตรงเส้นหนึ่งตัดเส้นตรงคู่หนึ่ง เส้นตรงคู่นั้นขนานกัน ก็ต่อเมื่อ มุมภายนอกและมุมภายในที่อยู่ตรงข้ามบนข้างเดียวกันของเส้นตัดมีขนาดเท่ากัน
มุมตรงมีขนาด 180 องศา
ขนาดของมุมภายในสามเหลี่ยมรวมกันได้ 180 องศา
ถ้าต่อด้านใดด้านหนึ่งของรูปสามเหลี่ยมออกไป แล้วมุมภายนอนกที่เกิดขึ้นจะมีขนาดเท่ากับผลบวกของขนาดของมุมภายในที่ไม่ใช่มุมประชิดของมุมภายนอกนั้น
ถ้ารูปสามเหลี่ยมสองรูปมีความสัมพันธ์กันแบบมุม-มุม-ด้าน คือ มีมุมที่ขนาดเท่ากันสองคู่และด้านที่อยู่ตรงข้ามกับมุมคู่ที่มีขนาดเท่ากัน ยาวเท่ากันหนึ่งคู่ แล้วรูปสามเหลี่ยมสองรูปนั้นเท่ากันทุกประการ
สมบัติของเส้นขนานกับมุมภายใน
- ถ้าเส้นตรงสองเส้นขนานกันและมีเส้นตัด แล้วขนาดมุมภายในที่อยู่บนข้างเดียวกันของเส้นตัดรวมกันเท่ากับ 180 องศา
- ถ้าเส้นตรงเส้นหนึ่งตัดกับเส้นตรงคู่หนึ่ง ทำให้ขนาดของมุมภายในที่อยู่บนข้างเดียวกันของเส้นตัดรวมกันเท่ากับ 180 องศา แล้วเส้นตรงคู่นั้นจะขนานกัน
มุมภายใน
ถ้ามีเส้นตรงเส้นหนึ่งตัดผ่านเส้นขนาน ทำให้เกิดมุมภายใน
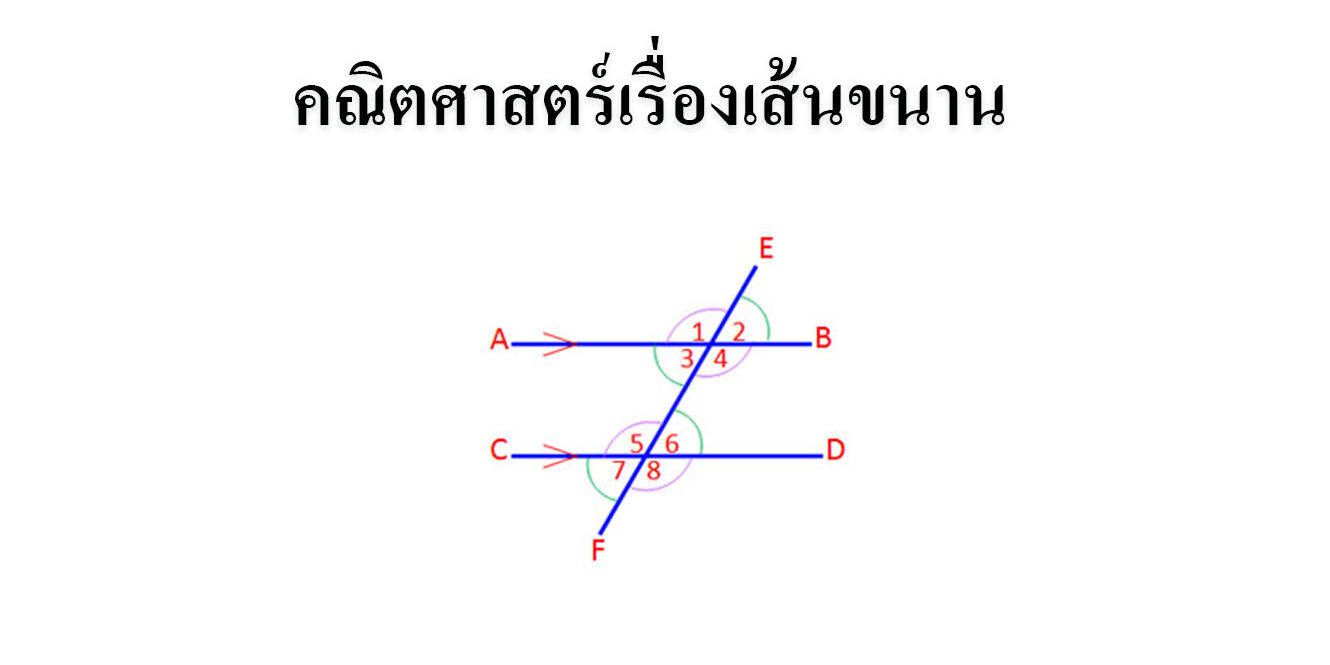
ถ้าเส้นตรง AB ขนานกับเส้นตรง CD แล้วมีเส้นตรงเส้นหนึ่งตัดผ่านเส้นขนาน ทำให้เกิดมุมภายในเกิดขึ้นดังรูป จะได้ว่า
มุม 1 กับ มุม 3 บวกกันได้ 180 องศา และ
มุม 2 กับ มุม 4 บวกกันได้ 180 องศา
มุมภายในเส้นขนาน และ มุมภายนอกเส้นขนาน

สามารถแบ่ง มุม 8 มุมบนเส้นขนานสองเส้น เป็น 2 กลุ่ม โดยใช้เส้นขนาน AB และ CD
กลุ่มที่ 1 มุมภายใน
หมายถึงมุมที่อยู่ภายในเส้นขนาน 2 เส้น
ได้แก่ มุม 3, มุม 4, มุม 5 และ มุม 6
กลุ่มที่ 2 มุมภายนอก
หมายถึงมุมที่อยู่ภายนอกเส้นขนาน 2 เส้น
ได้แก่ มุม 1, มุม 2, มุม 7 และ มุม 8
มุมด้านซ้ายของเส้นตัด และ มุมด้านขวาของเส้นตัด

เรียกเส้น EF ว่า ‘เส้นตัด’
เพราะเป็นเส้นที่ตัดเส้นขนาน 2 เส้น สามารถแบ่ง มุม 8 มุมบนเส้นขนานสองเส้น
เป็น 2 กลุ่ม โดยใช้เส้น EF
กลุ่มที่ 1 มุมด้านซ้ายของเส้นตัด
หมายถึงมุมที่อยู่ด้านซ้ายของเส้น EF
ได้แก่ มุม 1, มุม 3, มุม 5 และ มุม 7
กลุ่มที่ 2 มุมด้านขวาของเส้นตัด
หมายถึงมุมที่อยู่ด้านขวาของเส้น EF
ได้แก่ มุม 2, มุม 4, มุม 6 และ มุม 8
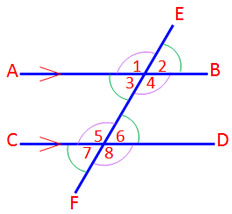
สรุป คุณสมบัติเกี่ยวกับมุมบนเส้นขนาน
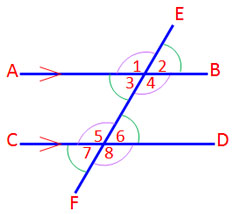
มุมแย้งเท่ากัน
มุม 3 = มุม 6
มุม 4 = มุม 5
มุมภายนอก = มุมภายใน
มุม 1 = มุม 5
มุม 3 = มุม 7
มุม 2 = มุม 6
มุม 4 = มุม 8
ผลบวกมุมภายใน = 180°
มุม 3 + มุม 5 = 180°
มุม 4 + มุม 6 = 180°