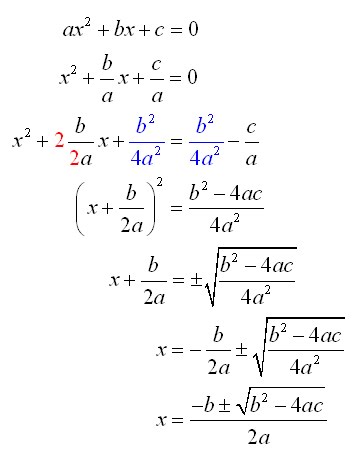สมการกำลังสองตัวแปรเดียว

สมการกำลังสอง คือ สมการพหุนามที่มีตัวแปรในพจน์ใดพจน์หนึ่ง ยกกำลังสองโดยมีรูปทั่วไปของสมการกำลังสอง ax² + bx+c = 0

เมื่อ a,b,c เป็นค่าคงตัว และ a 0 โดยมี x เป็นตัวแปร

เช่น   x² + 7x +12 = 0

จะได้ว่า a = 1 , b = 7, c = 12

          6x² -7x-5=0

จะได้ว่า a = 6 , b = -7, c = -5

                       x = 5x(x-1)

                        x = 5x²-x

                        5x²-2x= 0

จะได้ว่า a = 5 , b = -2, c = 0

ในการหาคำตอบของสมการกำลังสองจะกล่าวถึงวิธีการแก้สมการกำลัง 3 วิธีคือ

วิธีที่ 1 โดยวิธีการแยกตัวประกอบ

วิธีที่ 2 โดยวิธีการทำให้เป็นกำลังสองสมบูรณ์

วิธีที่ 3 โดยวิธีการใช้สูตร

สมการกำลังสองตัวแปรเดียว

สมการกำลังสองตัวแปรเดียว คือ สมการซึ่งมี x เป็นตัวแปร และมีรูปทั่วไปเป็น ax² + bx + c = 0 เมื่อ a, b, c เป็นค่าคงตัว และ a ไม่เท่ากับ 0

อย่างสมการกำลังสองตัวแปรเดียว 

1.) x² + 3x +5 = 0

จะได้ว่า a = 1 , b = 3, c = 5

2.) 2x² + 5x +  1 = 0

จะได้ว่า a = 2 , b = 5 , c = 1

3.) x² + 7x = 3

เมื่อ บวกด้วย บวกเข้าด้วย -3 ทั้งสองข้างของสมการ จะได้ x² + 7x + (-3)= 3+(-3) ดังนั้น x² + 7x – 3 = 0

จะได้ว่า a = 1, b = 2, c = -3

การแก้สมการกำลังสองโดยการแยกตัวประกอบ

สมมติว่าแยกตัวประกอบพหุนามได้เป็น (x + d)(x + e) = 0 เราสามารถสรุปได้ว่า x + d = 0 หรือ x + e = 0 โดยที่ d และ e เป็นค่าคงตัว

สมการกำลังสองจะมีจำนวนคำตอบได้ไม่เกิน 2 คำตอบ

เช่น

(x – 5)(x + 2) = 0 ดังนั้น x -5 = 0 ⇒ x = 5 หรือ x +2 = 0 ⇒ x = -2

(2x + 3)(3x + 6) = 0 ดังนั้น 2x +3 = 0 ⇒ x =  หรือ x + 2 = 0 ⇒ x = -2

ทำไมถึงรู้ว่า ในวงเล็บเท่ากับ 0 

ลองพิจารณา (x – 5)(x + 2) = 0

ให้ a แทน x – 5

b แทน x + 2

จะได้ว่า ab = 0 เราลองคิดง่ายๆเลย จำนวนที่คูณกันแล้วจะได้ 0 ต้องมีตัวใดตัวหนึ่งเป็น 0 แสดงว่าไม่ a ก็ b ต้องเท่ากับ 0 หรืออาจจะเป็น 0 ทั้ง a และ b

ดังนั้นเราจึงได้ว่า ab = 0 แล้ว a = 0 หรือ b = 0

นั่นคือ x – 5 = 0 หรือ x + 2 = 0

ซึ่งเราสามารถหาคำตอบ(หาค่า x)ของสมการกำลังสองนี้โดยใช้สูตรนี้