เรื่องที่เรียนเกี่ยวตรรกศาสตร์
- ประพจน์ จะกล่าวถึงความหมายและลักษณะของสิ่งที่เป็นประพจน์ และสิ่งที่ไม่เป็นประพจน์
- การเชื่อมประพจน์ จะนำประพจน์สองประพจน์ขึ้นไปมาดำเนินการ ซึ่งมี 5 การดำเนินการ ได้แก่ นิเสธ และ หรือ ถ้า…แล้ว… และ ก็ต่อเมื่อ
- การหาค่าความจริงของประพจน์ ประพจน์ต่าง ๆ จะมีค่าความจริงได้แก่ จริง และ เท็จ ซึ่งเราสามารถหาค่าความจริงของรูปแบบของประพจน์ใดๆ ได้
- สมมูลและนิเสธของประพจน์ จะกล่าวถึงรูปแบบของประพจน์ที่มีค่าความจริงตรงกันไม่ว่ากรณีใดๆ
- สัจนิรันดร์และการอ้างเหตุผล จะกล่าวถึงรูปแบบของประพจน์ที่มีค่าความจริงเป็นจริงเสมอ รวมไปถึงรูปแบบของประพจน์ที่แสดงถึงการอ้างเหตุผล ซึ่งมีส่วนของเหตุ และส่วนของผล
- ตัวบ่งปริมาณและประโยคเปิด จะกล่าวถึงรูปแบบและลักษณะของประโยคเปิดที่มีตัวบ่งปริมาณ รวมไปถึงการหาค่าความจริง สมมูล และนิเสธ
ตารางค่าความจริง
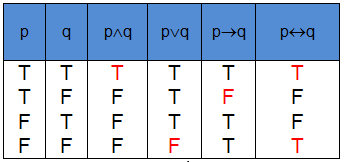
ตารางแสดงค่าความจริงของประพจน์ที่มีตัวเชื่อม พบเห็นบ่อยมากในเรื่องตรรกศาสตร์
ประพจน์ที่สมมูลกัน
ประพจน์ 2 ประพจน์จะสมมูลกัน ก็ต่อเมื่อ ประพจน์ทั้งสองมีค่าความจริงเหมือนกัน ทุกกรณีของค่าความจริงของประพจน์ย่อย
การทดสอบว่าประพจน์ 2 ประพจน์ สมมูลกัน ทำได้ 2 วิธีคือ
- สร้างตารางแจกแจงค่าความจริง ค่าความจริงต้องตรงกันทุกกรณี
- โดยการใช้หลักความจริงและประพจน์ที่สมมูลกันแบบง่ยๆที่ควรจำ เพื่อแปลงรูปประพจน์ไปเป็นแบบเดียวกัน
ตัวอย่างประพจน์ที่สมมูลกันที่ควรทราบ มีดังนี้
p ∧ q สมมูลกับ q ∧ p
p ∨ q สมมูลกับ q ∨ p
(p ∧ q) ∧ r สมมูลกับ p ∧ (q ∧ r)
(p ∨ q) ∨ r สมมูลกับ p ∨ (q ∨ r)
p ∧ (q ∨ r) สมมูลกับ (p ∧ q) ∨ ( p ∧ r)
p ∨ (q ∧ r) สมมูลกับ (p ∨ q) ∧ ( p ∨ r)
p → q สมมูลกับ ~p ∨ q
p → q สมมูลกับ ~q → ~p
p ⇔ q สมมูลกับ (p → q) ∧ (q → p)
ประพจน์ที่เป็นนิเสธกัน
ประพจน์ 2 ประพจน์เป็นนิเสธกัน ก็ต่อเมื่อ ประพจน์ทั้งสองมีค่าความจริงตรงข้ามกันทุกกรณีของค่าความจริงของประพจน์ย่อย
ตัวอย่างประพจน์ที่เป็นนิเสธกันที่ควรทราบ มีดังนี้
~(p ∧ q) สมมูลกับ ~p ∨ ~q
~(p ∨ q) สมมูลกับ ~p ∧ ~q
~(p → q) สมมูลกับ p ∧ ~q
~(p ⇔ q) สมมูลกับ (p ⇔ ~q) ∨(q ⇔ ~p)
~(p ⇔ q) สมมูลกับ (p ∧ ~q) ∨ ( q ∧~p)
สัจนิรันดร์
สัจจะ แปลว่าจริง ส่วนนิรันดร์ แปลว่าตลอดกาล ประพจน์ที่เป็นสัจนิรันดร์ คือ ประพจน์ที่มีค่าความจริงเป็นจริง ทุกกรณีของประพจน์ย่อย
ประโยคเปิด (Open Sentence)
คือข้อความที่อยู่ในรูปประโยคบอกเล่าหรือปฏิเสธ ที่มีตัวแปรและสื่อแทนค่าของตัวแปรนั้น จะได้ค่าความจริงแน่นอน หรือเป็นประพจน์ นิยมใช้สัญลักษณ์ P(x), P(x , y), Q(x , y) แทนประโยคเปิดที่มีตัวแปรระบุในวงเล็บ
ตัวบ่งปริมาณ (∀,∃)
ตัวบ่งปริมาณ เป็นตัวระบุจำนวนสมาชิกในเอกภพสัมพัทธ์ที่ทำให้ประโยคเปิดกลายเป็นประพจน์ ตัวบ่งปริมาณมี 2 ชนิด คือ
- ตัวบ่งปริมาณที่กล่าวถึง “สมาชิกทุกตัวในเอกภพสัมพัทธ์” ซึ่งเขียนแทนได้ด้วยสัญลักษณ์ “∀” อ่านว่า”สำหรับสมาชิก x ทุกตัว”
- ตัวบ่งปริมาณที่กล่าวถึง “สมาชิกบางตัวในเอกภพสัมพัทธ์” ซึ่งเขียนแทนได้ด้วยสัญลักษณ์ “∃” อ่านว่า “สำหรับสมาชิก x บางตัว”
วิธีการเขียนตัวบ่งปริมาณ
เราจะให้ P(x) แทนประโยคเปิด เราจะใช้สัญลักษณ์ ∀xP(x) และ ∃xP(x)
สมมติถ้าให้ P(x) แทน x+2 ≥ 2 และให้ U ∈ ℝ เมื่อ R หรือ ℝ เป็นเซตของจำนวนจริง
จะได้ ∀x[x+2 ≥ 2] อ่านว่า สำหรับ x ทุกตัว ที่ x+2 ≥ 2
และจะได้ ∃x[x+2 ≥ 2] อ่านว่า มี x บางตัว ที่ x+2 ≥ 2






