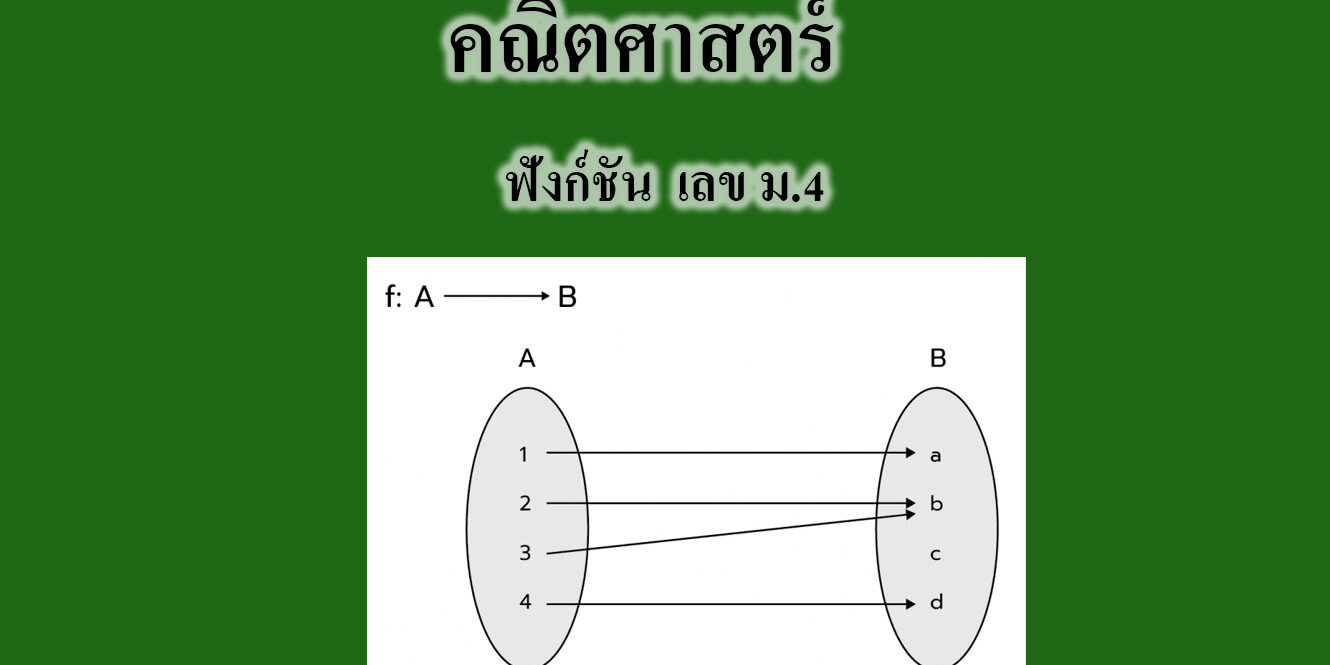
ฟังก์ชัน

ความสัมพันธ์และฟังก์ชัน

• ความสัมพันธ์
• โดเมนและเรนจ์
• ฟังก์ชัน

ความสัมพันธ์ที่กำหนดให้ในรูปแบบแจกแจงสมาชิก สามารถทำได้ดังตัวอย่างต่อไปนี้

ตัวอย่างที่ 1จงตรวจสอบว่าความสัมพันธ์ต่อไปนี้เป็นฟังก์ชันหรือไม่
f = {(0,1),(2,3),(4,5),(0,2)}
g ={(1,2),(7,8),(5,9),(1,2)}

โดเมนและเรนจ์

ความสัมพันธ์จาก A ไป B ให้ A และ B เป็นเซตใด ๆ แล้ว r เป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ AB เขียนได้ว่า r = {(a,b) | (a,b) ∈ A×B}

1. โดเมนของความสัมพันธ์ r  คือ  เซตของสมาชิกตัวหน้าในคู่อันดับของความสัมพันธ์  r

เขียนแทนด้วย  D_r

2. เรนจ์ของความสัมพันธ์  r  คือ  เซตของสมาชิกตัวหลังในคู่อันดับของความสัมพันธ์  r

เขียนแทนด้วย  R_r

3. การหาโดเมนและเรนจ์ของความสัมพันธ์   สามารถทำได้ดังนี้

3.1          กรณีความสัมพันธ์สามารถเขียนในรูปแจกแจงสมาชิกได้

โดเมน  คือ  สมาชิกตัวหน้าในคู่อันดับของความสัมพันธ์

เรนจ์  คือ  สมาชิกตัวหลังในคู่อันดับของความสัมพันธ์

3.2          กรณีความสัมพันธ์ไม่สามารถเขียนในรูปแจกแจงสมาชิกได้

3.2.1   การหาโดเมน   ควรเขียนความสัมพันธ์ให้อยู่ในรูปของ

y   =   เทอมของ  x

แล้วพิจารณาว่า  ภายในเซตที่กำหนดให้  x  มีค่าอะไรบ้างที่ทำให้หาค่า  y  ได้

โดยที่  y  นั้นต้องอยู่ภายในเซตที่กำหนดให้  ค่า  x  เหล่านั้นจะเป็นสมาชิก

ในโดเมน

3.2.2   การหาเรนจ์   ควรเขียนความสัมพันธ์ให้อยู่ในรูปของ

x   =   เทอมของ  y

แล้วพิจารณาว่า   y  มีค่าเป็นอะไรบ้างที่ทำให้หาค่า  x  ได้  โดยที่  x  นั้น

ต้องอยู่ภายในเซตที่กำหนดให้   ค่า  y  เหล่านั้น  จะเป็นสมาชิกในเรนจ์

การเขียนกราฟความสัมพันธ์แบบบอกเงื่อนไข

รูปแบบการเขียนแบบบอกเงื่อนไขจะเป็นเหมือนกับการเขียนเซตแบบบอกเงื่อนไข เช่น A = {x : x ∈ R} และ B = {y : y ∈ } เป็นต้น เรามักจะใช้ในกรณีที่ไม่สามารถเขียนแจกแจงสมาชิกทั้งหมดได้ กรณีที่ไม่สามารถแจกแจงสมาชิกได้ทั้งหมด เช่น x เป็นจำนวนจริง จะเห็นได้ว่าจำนวนจริงนั้นมีเยอะมาก บอกไม่หมดแน่ๆ จึงต้องเขียนแบบบอกเงื่อนไขนั่นเอง

เรามาดูตัวอย่างการเขียนกราฟกันค่ะ

ให้ A = {x : x ∈ R} และ B = {y : y ∈ R}

กำหนด r ⊂ A × B และ r = {(x, y) ∈ A × B : y = 2x²+1}

ขั้นที่ 1 ให้ลองแทนค่าของจำนวนเต็มบวก x ลงในสมการ y = x²  ที่ต้องแทน x เป็นจำนวนเต็มบวก เพราะเงื่อนไขในเซต A นั่นเอง

แทน x = 0, 1, 2, 3, 4

x = 0 ; y = 1

x = 1 ; y = 2(1)²+1 = 3

x = 2 ; y =2 (2)² +1= 9

x = 3 ; y = 2(3)² +1= 19

x = 4 ; y = 2(4)² +1= 33

ขั้นที่ 2 เมื่อเราแทนค่า และได้ค่า y มาแล้ว ให้เราเขียนคู่อันดับที่เราได้จากขั้นที่ 1

จะได้คู่อันดับ ดังนี้ (0, 1), (1, 3), (2, 9), (3,19), (4, 33)

กราฟของความสัมพันธ์ ในรูปแบบกำลังสอง

ให้ x, y เป็นจำนวนจริงใดๆ สมการ y = ax² + bx +c เป็นสมการกำลังสอง ซึ่งเป็นสมการพาราโบลาที่เราเคยเรียนมาตอนม.ต้นนั่นเอง

ให้  = {(x, y) : y = 3x²+1}

หรือ ถ้าให้ = {(x, y) : y = x² + 2x + 9}

นิยาม 3 ให้ R เป็นความสัมพันธ์ บนเซต A จะเรียก R ว่า มีสมบัติสะท้อน(reflexive )
ถ้า (a,a) ฮ R สำหรับทุก ๆ สมาชิก a ฮ A

ตัวอย่างที่ 7 พิจารณาความสัมพันธ์บน {1, 2, 3, 4} ต่อไปนี้

R₁ = {(1,1),(1,2),(2,1),(2,2),(3,4),(4,1),(4,4)}
R₂ = {(1,1),(1,2),(2,1)}
R₃ = {(1,1),(1,2),(1,4),(2,1),(2,2),(3,3),(4,1),(4,4)}
R₄ = {(2,1),(3,1),(3,2),(4,1),(4,2),(4,3)}
R₅ ={(1,1),(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),(3,3),(3,4),(4,4)}
R₆ = {(3,4)}
ความสัมพันธ์ใดมีสมบัติสะท้อน ?

วิธีทำ

                ความมสัมพันธ์ R₃และ R₅ มีสมบัติการสะท้อน เพราะทั้งคู่มีคู่ลำดับ
(a,a) ทุก a ใน {1, 2, 3, 4} คือ (1,1), (1,2), (3,3) และ (4,4)
ส่วนความสัมพันธ์อื่นนั้นไม่มีสมบัติการสะท้อน

ตัวอย่างที่ 8 ความสัมพันธ์ใดจากตัวอย่างที่ 5 มีสมบัติสะท้อน ?

วิธีทำ

ความสัมพันธ์ที่มีสมบัติสะท้อน คือ R₁ , R₃ และ R₄
ความสัมพันธ์อื่นนั้นไม่มีสมบัติการสะท้อน

ตัวอย่างที่ 9 ความสัมพันธ์ภายใต้การหาร บนเซตของจำนวนเต็มบวกมีสมบัติสะท้อน หรือไม่

วิธีทำ

จาก a | a ทุก a ที่เป็นจำนวนเต็มบวก
ดังนั้น ความสัมพันธ์ดังกล่าว มีสมบัติสะท้อนนิยาม 4 ความสัมพันธ์ R บนเซต A เรียกว่า
มีสมบัติสมมาตร ( Symmetric) ถ้า (a,b) ∈R แล้ว (b,a) ∈ R
มีสมบัติปฎิสมมาตร (Antisymmetric) ถ้า (a,b) ∈ R และ (b,a) ∈ R แล้ว a = b

ตัวอย่างที่ 10 ความสัมพันธ์ใดในตัวอย่างที่ 7 มีสมบัติสมมาตร ( Symmetric) และ
ความสัมพันธ์ใดมีสมบัติปฎิสมมาตร (Antisymmetric)?

วิธีทำ ความสัมพันธ์ R₂ และ R₃ มีสมบัติสมมาตร ( Symmetric)

ความสัมพันธ์ R₄ ,R₅ และ R₆ มีสมบัติปฎิสมมาตร (Antisymmetric)

ตัวอย่างที่ 11 ความสัมพันธ์ใดในตัวอย่างที่ 5 มีสมบัติสมมาตร ( Symmetric) และ
ความสัมพันธ์ใดมีสมบัติปฎิสมมาตร (Antisymmetric)?

วิธีทำ

ความสัมพันธ์ R₃ ,R₄ และ R₆ มีสมบัติสมมาตร ( Symmetric)R₃ มีสมบัติสมมาตร ( Symmetric) เพราะ ถ้า a = b หรือ a = -b แล้ว b= a หรือb = – a
R₄ มีสมบัติสมมาตร ( Symmetric) เพราะ ถ้า a = b แล้ว b = a
R₆ มีสมบัติสมมาตร ( Symmetric) เพราะ ถ้า a + b ฃ 3 แล้ว b + a ฃ 3
ผู้อ่านควรตรวจสอบดูว่าความสัมพันธ์อื่นไม่มีสมบัติสมมาตร
ความสัมพันธ์ R₁ ,R₂ , R₄ และ R₅ มีสมบัติปฎิสมมาตร (Antisymmetric)
R₁ มีสมบัติปฎิสมมาตร เพราะ ถ้า a ฃ b และ b ฃ a แล้ว a = b
R₂ มีสมบัติปฎิสมมาตร เป็นไปไม่ได้ที่ a > b และ b > a จะเป็นจริง
R₄ มีสมบัติปฎิสมมาตร เพราะ ทั้ง 2 ค่า (a และ b) มีความสัมพันธ์บน R₄ แล้ว a = b
R₅ มีสมบัติปฎิสมมาตร เพราะจะเป็นไปไม่ได้ที่ a = b + 1 และ b = a +1
ผู้อ่านควรตรวจสอบว่าความสัมพันธ์อันอื่นไม่มี สมบัติปฎิสมมาตรตัวอย่างที่ 12 ความสัมพันธ์ภายใต้การหาร บนเซตของจำนวนเต็มบวกมีสมบัติสมมาตร และ
ปฎิสมมาตร หรือไม่

วิธีทำ

ความสัมพันธ์นี้ ไม่มีสมบัติสมมาตร เพราะ 1 หาร 2 แต่ 2 ไม่หาร 1
แต่ มีสมบัติปฎิสมมาตร เพราะ สำหรับ a และ b เป็นจำนวนเต็มบวก
ถ้า a | b และ b | a แล้ว a = b

นิยาม 5 ความสัมพันธ์ R บนเซต A จะเรียกว่ามีสมบัติถ่ายทอด
ถ้า (a ,b) ∈ R และ (b ,c) ∈ R แล้ว (a ,c) ∈ R ทุก a, b, c ∈ A

ตัวอย่างที่ 16 จงหาจำนวนความสัมพันธ์ที่มีสมบัติสะท้อน บนเซตที่มีจำนวนสมาชิก n ตัว

วิธีทำ
ถ้า R เป็นความสัมพันธ์ที่มีสมบัติสะท้อนดังนั้น R ต้องมีสมาชิกอย่างน้อย n คู่อันดับ
คือ (a,a) ทุก a ฮ A ดังนั้นยังเหลืออีก n(n-1) คู่อันดับอื่น ๆ ในรูป (a,b) ซึ่ง a น b
อาจจะอยู่หรือไม่อยู่ใน R ก็ได้ ซึ่งจะมี 2^n(n-1) เซตย่อยที่ต่างกัน นำมา ผนวกกับ R
ดังนั้น จึงมี 2^n(n-1) ความสัมพันธ์ที่มีสมบัติสะท้อน

ผลคูณคาร์ทีเชียน

เป็นการกระทำกันระหว่างเซต 2 เซต โดยผลคูณคาร์ทีเชียนระหว่างเซต A และ B เขียนแทนด้วย A×B คือ เซตของคู่อันดับ (a,b) ทั้งหมด โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B เขียนอยู่ในรูปแบบ

A×B = {(a,b) | a ∈ A และ b ∈ B}

สมบัติของผลคูณคาร์ทีเชียน

ให้ A, B และ C เป็นเซตใด ๆ และ n(A) คือ จำนวนสมาชิกของเซต A

• A×{} = {}
• {}×A = {}
• A×(B∪C) = (A×B)∪(A×C)
• A×(B∩C) = (A×B)∩(A×C)
• A×(B-C) = (A×B) – (A×C)
• n(A×B) = n(A).n(B)

พิจารณาความสัมพันธ์

r₁   =   {(1,2),(2,3),(3,4),(4,5)}

r₂  =   {(x,y) ∈ I⁺x I⁺ | y = x }

เซตสมาชิกตัวหน้าของความสัมพันธ์  r ₁  คือ  {1,2,3,4}  เรียกเซตนี้ว่า   โดเมนของ r₁

เซตสมาชิกตัวหลังของความสัมพันธ์  r ₁  คือ  {2,3,4,5}  เรียกเซตนี้ว่า   เรนจ์ของ r₁

ส่วน  r₂ มีโดเมนและเรนจ์เท่ากับจำนวนเต็มบวก

บทนิยาม    ให้  r  เป็นความสัมพันธ์จาก  A ไป B

โดเมนของ  r  คือเซตของสมาชิกตัวหน้าของคู่อันดับใน r  เขียนแทนด้วย  D_r

เรนจ์ของ  r   คือเซตของสมาชิกตัวหลังของคู่อันดับใน r   เขียนแทนด้วย  R _r