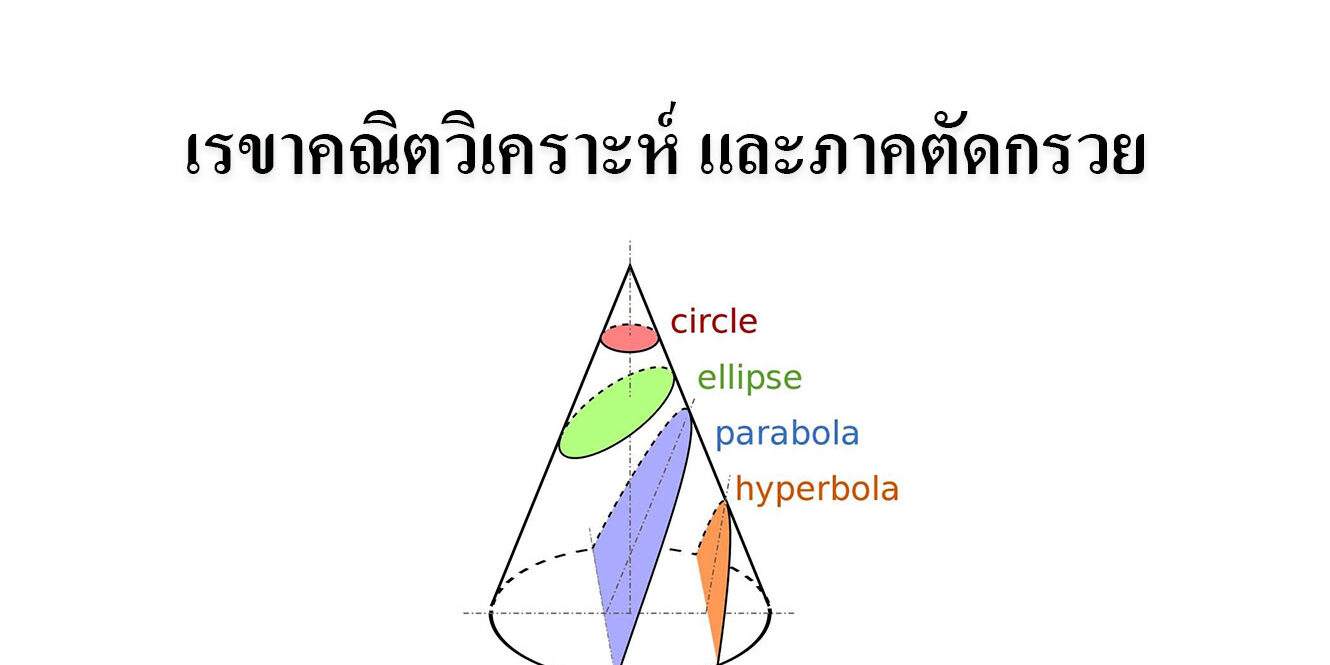
เรขาคณิตวิเคราะห์ และภาคตัดกรวย

เรขาคณิตวิเคราะห์ และภาคตัดกรวย

1. ความรู้เบื้องต้นเกี่ยวกับเรขาคณิตวิเคราะห์
2. ระยะทางระหว่างจุดสองจุด
3. จุดกึ่งกลางระหว่างจุดสองจุด
4. ความชันของเส้นตรง
5. เส้นขนาน
6. เส้นตั้งฉาก
7. ความสัมพันธ์ซึ่งมีกราฟเป็นเส้นตรง
8. ระยะห่างระหว่างเส้นตรงกับจุด
9. ภาคตัดกรวย
10. วงกลม
11. วงรี
12. พาราโบลา (Parabola)
13. ไฮเพอร์โบลา (Hyperbola)
14. การเลื่อนกราฟ

รขาคณิตวิเคราะห์ (Analytic Geometry) เป็นคณิตศาสตร์ แขนงหนึ่งที่กล่าวถึงจุดบนระนาบ (point and plane)

               เรขาคณิตวิเคราะห์จึงแบ่งได้ดังนี้

           1. ระบบพิกัดฉาก ประกอบด้วยเส้นตรง สองเส้นเส้นหนึ่งอยู่ในแนวนอน เรียกว่า แกน x อีกเส้นหนึ่งอยู่ในแนวตั้งเรียกว่าแกน y ทั้งสองเส้นนี้ตัดกันเป็นมุมฉาก และเรียกจุดตัดว่า จุดกำเนิด y ควอดรันต์ที่ II ควอดรันต์ที่ I (-,+) (+,+) x ควอดรันต์ที่ III ควอดรันต์ที่ IV (-,-) (+,-) 2. การหาระยะทางระหว่างจุด 2 จุด ถ้า P(x1,y1) และ P(x2,y2) เป็นจุด 2 จุดในระนาบ ระยะทางระหว่างจุด P และจุด Q หาได้โดย

PQ = (x2-x1)2 + (y2-y1) 2

3. จุดกึ่งกลางระหว่างสองจุด ถ้า P(x1,y1) และ P(x2,y2) เป็นจุด 2 จุดในระนาบและให้ M(x,y) เป็นจุดกึ่งกลางระหว่าง P และ Q เราสามารถหาจุด M ได้ดังนี้ จุดกึ่งกลาง M คือ x1+ x2 , y1+ y2 2 2
4. สมการของเส้นตรง Q(x2,y2) 4.1 ความชัน(slop)=tanq=m Q(x1,y1)
   ความชัน = m = y2 – y1 x2 – x1

4.2 สมการเส้นตรงที่ผ่านจุด (x1,y1) และมีความชันเท่ากับ m คือ    y – y1 = m(x – x1)

4.3 สมการเส้นตรงที่มี y -intercept เท่ากับ b และมีความชันเท่ากับ m คือ y = mx + b

4.4 จาก 4.2 และ 4.3 สามารถเขียนสมการเส้นตรงใหม่ในรูปของ  Ax + By + C = 0

วิธีการหาความชันของ

Ax + By + C = 0

m=-A/B ตัวอย่าง จงหาความชันของเส้นตรง 3x + 4y – 5 = 0 วิธีทำ4y = -3x + 5 y = -(-3/4)x +(5/4) \ ความชันคือ -3/4 4.5 เส้นตรง l1 ขนานกับ l2 ก็ต่อเมื่อ m1=m2 เส้นตรง l1 ตั้งฉากกับ l2 ก็ต่อเมื่อ m1m2 = -1 5. การหาระยะทางจากจุดไปยังเส้นตรง กำหนดให้ l เป็นเส้นตรงที่มีสมการ Ax + By + C = 0 และ P(x1,y1) เป็นที่อยู่นอกเส้น l ดังรูป

P(x1,y1) d l Ax + By + C = 0

ระยะทางระหว่างจุดสองจุด

บนระบบพิกัดฉาก กำหนดจุด P 1 (x 1 ,y 1 )และจุด P 2 (x 2 ,y 2 ) อยู่บนเส้นตรง
เดียวกัน การหาระยะทางระหว่างจุด P 1และ จุด P 2สามารถหาได้ตามเงื่อนไขของพิกัดจุด
บนเส้นตรงดังนี้

กำหนด d แทน ระยะทางระหว่างจุด P 1 และ จุด P 2

ความชันของเส้นตรง

AB มีค่าเท่ากับ m = (y₂ – y₁)/(x₂ – x₁)