Tuemaster เรียนออนไลน์ ม.ปลาย

เนื้อหาที่สอน เลข ม.4 เทอม 1 เรื่องเซต

เซต

(1) เซต

(2) เอกภพสัมพัทธ์

(3) สับเซตและเพาเวอร์เซต

(4) ยูเนียน อินเตอร์เซกชันและคอมพลีเมนต์ของเซต

ตอนที่ 1 : พื้นฐานของเซต

ประเภทของเซต เอกภพสัมพัทธ์ และ คุณสมบัติพื้นฐาน

เซต คืออะไร และเราต้องมีเอกภพสัมพัทธ์ไว้ทำอะไร เซตจำกัด เซตอนันต์ต่างกันอย่างไร ต้องรู้

การหาจำนวนสมาชิกในเซต n(A)

มีเซตก็ต้องหาเป็นว่าสมาชิกมีอะไรบ้าง พอโจทย์ยาก ๆ มันจะหาสมาชิกยากมากขึ้น ดังนั้น มีทริคยังไงต้องรู้ เช่น {{},{3},{1,2},{2,1},{{}}}

ให้A เป็นเซตจำกัด เราจะใช้ n(A) แทนจำนวนสมาชิกของเซต A

เช่น A = {a,b,c,d} จะได้ n(A) = 4

B = {5,6,7,8,9,10} จะได้ n(B) = 6

จำนวนสมาชิกของเซตจำกัดสองเซต

กรณีที่ 1 ถ้า A และ B เป็นเซตที่ไม่มีสมาชิกร่วมกัน

จะได้ว่า n(A∪B) = n(A)+n(B)

เช่น ให้ A = {1,2,3,4,5}, B = {6,7,8,9,10} จะได้ n(A) = 5, n(B) = 5

พิจารณา A∪B = {1,2,3,4,5,6,7,8,9,10} จะได้ n(A∪B) = 10

พิจารณา n(A)+n(B) = 5+5 = 10

สับเซต ⊂

สับเซต คือ เซตย่อยทั้งหมด หลักการคือให้นึกเหมือนกับว่าเราไปร้านขายของและกำลังเลือกซื้อของอยู่

เพาเวอร์เซต P(A)

เพาเวอร์เซต คือ เซต ของ สับเซต จำนวนสมาชิกของเพาเวอร์เซต ก็คือสับเซตทั้งหมดที่เป็นไปได้ หรือ 2 P(A) นั่นเอง

พาวเวอร์เซต

หมายถึง เซตของสับเซต จะเขียนแทนเพาเวอร์เซตของเซต A ด้วย P(A)

วิธีหาเพาเวอร์เซต จะต้องหาสับเซตทั้งหมดให้ได้ก่อน จากนั้นจึงใส่เซตครอบลงไป

ตัวอย่าง จงหาสับเซตทั้งหมดของ A = {2, 4, 6, 8}

ขั้นแรก : หาสับเซตก่อน ได้แก่

Ø , {2} , {4} , {6} , {8} , {2, 4} , {2, 6} , {2, 8} , {4, 6} , {4, 8} , {6, 8} , {2, 4, 6} , {2, 6, 8} , {2, 4, 8} , {4, 6, 8} , {2, 4, 6, 8}

ดังนั้น P(A) = {Ø, {2},{4},{6},{8},{2, 4},{2, 6},{2, 8},{4, 6},{4, 8},{6, 8}, {2, 4, 6}, {2, 6, 8},{2, 4, 8},{4, 6, 8},{2, 4, 6, 8}

กำหนดให้ A เป็นเซตจำกัด ถ้าเซต A มีจำนวนสมาชิก ตัวแล้วจำนวนสมาชิกของเพาเวอร์เซต A จะเท่ากับ 2ⁿตัว

ตัวอย่าง

1. ถ้า P(P(A)) มีสมาชิก 256 ตัว แล้วเซต A จะมีสมาชิกกี่ตัว

วิธีทำ

P(P(A)) = 256 = 2^8

P(A) = 8= 2^3

n(A) = 3

2. ถ้า n(P(A)) – n(P(B)) = 63 และn(P(A∩B)) + n(P(A∪B)) = n(P(C∩B)) + n(P(C∪B)) แล้ว จงหาค่าของ n(A) + n(B) + n(C)

ตะลุยโจทย์รวม สมาชิก สับเซต เพาเวอร์เซต

หลังจากความรู้พื้นฐานกันมานิดนึงแล้ว เราไปดูโจทย์รวมเพื่อความเข้าใจที่มากขึ้นที่ช่อง Youtube กันได้เลย

ตอนที่ 2 : ตัวดำเนินการเซต และ แผนภาพเวนน์

แผนภาพเวนน์ ออยเลอร์

ถือเป็นพระเอกในเรื่องเซตเลยก็ว่าได้ครับ เพราะ แผนภาพเวนน์จะช่วยเราได้เกือบทุกโจทย์ โดยหลักการมองเป็นภาพ

ตัวดำเนินการของเซต∩,∪,−,′

เมื่อมีเซตหลาย ๆ เซต เราจะมีตัวดำเนินการ เพื่อกระทำกันระหว่างเซต เกิดเป็นเซตใหม่ มีตัวหลักและวิธีการจำอย่างไรต้องรู้

สมบัติของการดำเนินการทางเซต

สมบัติก็เหมือน ความเท่ากัน ดังนั้น มันจะช่วยเราในเรื่องการพิสูจน์สูตร หรือ การลดรูปเป็นรูปอย่างง่ายนั่นเองครับ

โจทย์ปัญหานับจำนวนสมาชิกโดยใช้แผนภาพเวนน์

โจทย์คลาสสิกในเรื่อง เซต คือ การหา “จำนวน” ของอะไรบางอย่าง เช่น จำนวนคนที่ชอบเรียนคณิตอย่างเดียว ฯลฯ โดยเราจะใช้แผนภาพเวนน์มาช่วย

สับเซต และ เพาเวอร์เซต

สับเซต (subset) หรือ “เซตย่อย” คือ เซตที่เล็กกว่าหรือเท่ากันกับเซตที่กำหนด โดยต้องใช้สมาชิกร่วมกับเซตที่กำหนดเท่านั้น

สัญลักษณ์ที่ใช้แทนประโยค “ A เป็นสับเซตของ B” คือ A Ì B และจะเกิดขึ้นได้ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A นั้นเป็นสมาชิกของเซต B ด้วย หรือเมื่อ A เป็นเซตว่างก็ได้

เช่น {1,2}Ì{1,2,3}เนื่องจากทั้ง 1 และ 2 เป็นสมาชิกของ {1,2,3}

รูปแบบ เซต (เล็ก) Ì เซต(ใหญ่)

สมบัติของซับเซต

1. A ⊂ A (เซตทุกเซตเป็นสับเซตของตัวมันเอง)

2. A ⊂ U (เซตทุกเซตเป็นสับเซตของเอกภพสัมพัทธ์)

3. Ø ⊂ A (เซตว่างเป็นสับเซตของทุกๆ เซต)

4. ถ้า A ⊂ ø แล้ว A = ø

5. ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C (สมบัติการถ่ายทอด)

6. A = B ก็ต่อเมื่อ A ⊂ B และ B ⊂ A

7. ถ้า A มีจำนวนสมาชิก n ตัว สับเซตของเซตจะมีทั้งสิ้น 2n สับเซต

การหาสับเซตทั้งหมดของA

จำนวนสับเซตทั้งหมดหาได้จาก 2ⁿ เมื่อ n = จำนวนสมาชิกในเซต

ตัวอย่าง จงหาสับเซตทั้งหมดของ A เมื่อ A = {2, 4, 6, 8}

A จะมีสับเซตทั้งหมด 2⁴ =16 สับเซต เมื่อแจกแจงสับเซตทั้งหมดจะได้ดังนี้

{2} {4} {6} {8}

{2, 4} {2, 6} {2, 8} {4, 6} {4, 8} {6, 8}

{2, 4, 6} {2, 6, 8} {2, 4, 8} {4, 6, 8}

{2, 4, 6, 8}

ยูเนียน อินเตอร์เซกชันและคอมพลีเมนต์ของเซต

ยูเนียน (Union)
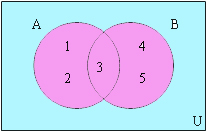
ยูเนียน (Union) มีนิยามว่า เซต A ยูเนียนกับเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ เซต B หรือทั้ง A และ B สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B
ตัวอย่างเช่น
A ={1,2,3}
B= {3,4,5}
∴ A ∪ B = {1,2,3,4,5}
เราสามารถเขียนการยูเนี่ยนลงในแผนภาพได้ดังนี้

อินเตอร์เซกชัน (Intersection)
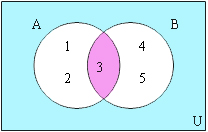
อินเตอร์เซกชัน (Intersection) มีนิยามคือ เซต A อินเตอร์เซกชันเซต B คือ เซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B
ตัวอย่างเช่น
A ={1,2,3}
B = {3,4,5}
∴ A ∩ B = {3}
เราสามารถเขียนการอินเตอร์เซกชันลงในแผนภาพได้ดังนี้

คอมพลีเมนต์ (Complements)
คอมพลีเมนต์ (Complements) มีนิยามคือ ถ้าเซต A ใดๆ ในเอกภพสัมพัทธ์ U แล้วคอมพลีเมนต์ของเซต A คือ เซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่เป็นสมาชิกของ A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A’