ตรรกศาสตร์ เรื่องสมบัติการสมมูล
ประพจน์ที่สมมูล
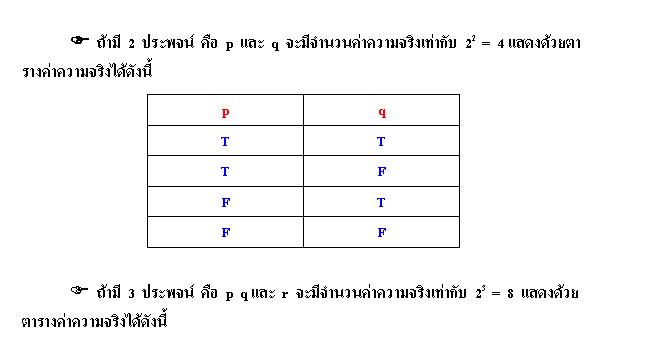
ประพจน์ที่สมมูลกัน คือ ประพจน์ที่มีค่าความจริงเหมือนกันทุกกรณี เขียนแทนด้วยสัญลักษณ์ “≡” ค่าความจริงของประพจน์ p→q และ ∼q→∼p จากตารางค่าความจริง
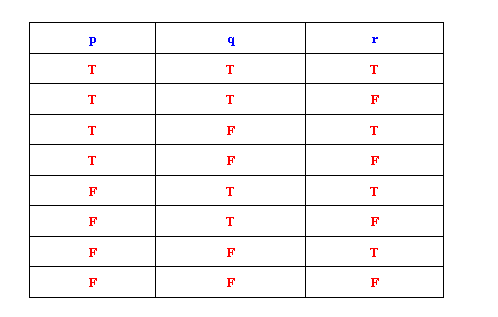
การแจกแจงค่าความจริง ตรรกศาสตร์

สมบัติการสมมูล
- สมบัติการเปลี่ยนกลุ่ม
p ∧ ( q ∧ r ) ≡ ( p ∧ q ) ∧ r ≡ p ∧ q ∧ r
p ∨ ( q ∨ r ) ≡ ( p ∨ q ) ∨ r ≡ p ∨ q ∨ r
p ↔ ( q ↔ r ) ≡ ( p ↔ q ) ↔ r ≡ p ↔ q ↔ r
- สมบัติการแจกแจง
p ∧ ( q ∨ r ) ≡ ( p ∧ q ) ∨ ( p ∧ r )
p ∨ ( q ∧ r ) ≡ ( p ∨ q ) ∧ ( p ∨ r )
p → ( q ∨ r ) ≡ ( p → q ) ∨ ( p → r )
p → ( q ∧ r ) ≡ ( p → q ) ∧ ( p → r )
( p ∨ q ) → r ≡ ( p → r ) ∧ ( p → r )
( p ∧ q ) → r ≡ ( p → r ) ∨ ( p → r )
- สมบัติการสลับที่
p ∧ q ≡ q ∧ p
p ∨ q ≡ q ∨ p
p ↔ q ≡ q ↔ p
- สมบัติของ ถ้า…แล้ว ( → )
p → q ≡ ~q → ~p ≡ ~p ∨ q
- สมบัติของ ก็ต่อเมื่อ ( ↔ )
p ↔ q ≡ ( p → q ) ∧ (q → p )
- สมบัติของ นิเสธ ( ~ )
~(~p) ≡ p
~(p ∧ q) ≡ ~p ∨ ~q
~(p ∨ q) ≡ ~p ∧ ~q
~(p → q) ≡ p ∧ ~q
~(p ↔ q) ≡ ~p ↔ q ≡ p ↔ ~q
- สมบัติอื่น ๆ
p ∧ p ≡ p
p ∧ T ≡ p
p ∧ F ≡ F
p ∧ ~p ≡ F
p ∨ p ≡ p
p ∨ T ≡ T
p ∨ F ≡ p
p ∨ ~p ≡ T
p → F ≡ ~p
F → p ≡ T
p → T ≡ T
T → P ≡ P
P ↔ P ≡ T
P ↔ ∼P ≡ F






