เนื้อหาคณิตศาสตร์ ม.4 เรื่องเซต

เนื้อหาคณิตศาสตร์ ม.4 เรื่องเซต แบบเต็มคาราเบล

ความหมายของเซต
เซตจำกัด และเซตอนันต์
เซตว่าง และเอกภพสัมพัทธ์
ยูเนียน อินเตอร์เซกชันและคอมพลีเมนต์ของเซต
สับเซตและเพาเวอร์เซต
แผนภาพเวนน์-ออยเลอร์

เซต (Set)
ความหมายของเซต
ในทางคณิตศาสตร์ คำว่า “เซต” หมายถึง กลุ่ม หมู่ เหล่า กอง ฝูง ชุด เเละเมื่อกล่าวถึงเซตของสิ่งใดๆ จะทราบได้ทันทีว่าในเซตนั้นมีอะไรบ้าง เราเรียกสิ่งที่อยู่ในเซตว่า ‘สมาชิก’
สัญลักษณ์ที่ใช้แทนเซต ชื่อเเละสมาชิกของเซต

1. สามารถใช้วงกลม, วงรี แทนเซตต่างๆ ได้

2. ชื่อเซตนิยมใช้ตัวใหญ่ทั้งหมด เช่น A, B, C, …

3. สัญลักษณ์ ∈ แทนคำว่า ” เป็นสมาชิกของ ”
∉ แทนคำว่า ” ไม่เป็นสมาชิกของ ”

ลักษณะของเซต

เซตว่าง (Empty Set) คือ เซตที่ไม่มีสมาชิก เขียนแทนด้วย ” { } ” หรือ ∅
เช่น เซตของจำนวนเต็มที่อยู่ระหว่าง 1 กับ 2

เซตของสระในคำว่า ” อรวรรณ ”

เซตจำกัด (Finite Set) คือ เซตที่สามารถบอกจำนวนสมาชิกได้
เช่น ∅ มีจำนวนสมาชิกเป็น 0
{ 1, 2, 3, … , 50 } มีจำนวนสมาชิกเป็น 50
เซตอนันต์ (Infinite Set) คือ เซตที่ไม่ใช่เซตจำกัด ไม่สามารถบอกจำนวนสมาชิกได้

เช่น เซตของจำนวนเต็มบวก {1, 2, 3, 4, … }

เซตของจุดบนระนาบ

การเขียนเซต

1. การเขียนแบบแจกแจงสมาชิก (Tabular form)
หลักการเขียน
1. เขียนสมาชิกทั้งหมดในวงเล็บปีกกา
2. สมาชิกเเต่ละตัวคั่นด้วยเครื่องจุลภาค (,)
3. สมาชิกที่ซ้ำกันให้เขียนเพียงตัวเดียว
4. ในกรณีที่มีจำนวนสมาชิกมากๆ ให้เขียนสมาชิกอย่างน้อย 3 ตัว เเล้วใช้จุด 3 จุด (Tripple dot) เเล้วจึงเขียนสมาชิกตัวสุดท้าย

2. การเขียนเซตแบบบแกเงื่อนไขของสมาชิกในเซต (Set builder form)

นิยามของเซตอนันต์

รู้จักเซตจำกัดกันแล้ว มาต่อที่เซตอนันต์ (infinite set) กันได้เลย โดยเซตอนันต์ คือ เซตที่ไม่สามารถเขียนแจกแจงสมาชิกได้ หรือเป็นเซตที่มีสมาชิกมากมายนับไม่ถ้วน มาดูตัวอย่างของเซตอนันต์กัน

ตัวอย่างที่ 3

C = {c | c เป็นจำนวนจริงที่น้อยกว่า 888 }

จะเห็นว่าเซต C มีสมาชิกเป็นจำนวนจริงมากมายนับไม่ถ้วน เพราะรวมทั้งเศษส่วน ทศนิยม และตัวเลขอื่น ๆ ที่เป็นจำนวนจริง และมีค่าน้อยกว่า 999 ดังนั้น เราจึงไม่สามารถนับจำนวนสมาชิก หรือเขียนแจกแจงสมาชิกให้กับเซต C ได้ จะได้ว่าเซต C เป็นเซตอนันต์

ข้อสังเกตเกี่ยวกับเซตจำกัด และเซตอนันต์

1. การมีสัญลักษณ์ … ไม่ได้บอกว่าเซตนั้น ๆ เป็นเซตจำกัด หรือเซตอนันต์

• เซตจำกัด

บทนิยาม เซตจำกัด คือ เซตที่สามารถระบุจำนวนสมาชิกในเซตได้

ตัวอย่างเช่น

A = {1, 2, 3, 4, 5} มีสมาชิก 5 สมาชิก

B = { a, e, i, o, u} มีสมาชิก 5 สมาชิก

• เซตอนันต์

เซตอนันต์ คือ เซตที่ไม่ใช่เซตจำกัด หรือเซตที่มีจำนวนสมาชิกมากมายนับไม่ถ้วน

ตัวอย่างเช่่น

C = {…,-2,-1,0,1,2,…}

• เซตที่เท่ากัน

เซต A และเซต B จะเป็น เซตที่เท่ากัน ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B
และสมาชิกทุกตัวของเซต B เป็นสมาชิกทุกตัวของเซต A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A= B

ตัวอย่างเช่่น

A = {1, 2, 3, 4, 5}

B = { x | x เป็นจำนวนนับที่มีค่าน้อยกว่าหรือเท่ากับ 5}

∴ A = B

• เซตว่าง

เซตว่าง คือ เซตที่ไม่มีสมาชิก หรือมีจำนวนสมาชิกในเซตเป็นศูนย์ สามารถเขียนแทนได้ด้วยสัญลักษณ์ {} หรือ Ø

ตัวอย่างเช่่น

A = {x | x เป็นจำนวนเต็ม และ 1 < x < 2} ∴ A = Ø

B = { x | x เป็นจำนวนเต็มบวก และ x + 1 = 0 } ∴ ฺB = Ø

เนื่องจากเราสามารถบอกจำนวนสมาชิกของเซตว่างได้ ดังนั้น เซตว่างเป็นเซตจำกัด

เซตว่าง
• เซตที่ไม่มีสมำชิก หรือมีจ ำนวนสมำชิกในเซตเป็นศูนย์
• ตัวแปรอำร์เรย์ที่ไม่ได้ก ำหนดค่ำ
• คุณสมบัติของเซตว่ำง เช่น ∅ ⊆ A, A ∪ ∅ = A, A ∩ ∅ = ∅, A ⊆ ∅ ⇒ A = ∅

• เอกภพสัมพัทธ์

เอกภพสัมพัทธ์ คือ เซตที่ประกอบด้วยสมาชิกทั้งหมดของสิ่งที่เราต้องการจะศึกษา สามารถเขียนแทนได้ด้วยสัญลักษณ์ u

ตัวอย่างเช่่น ถ้าเราจะศึกษาเกี่ยวกับจำนวนเต็ม

U = {…,-2,-1,0,1,2,…}

หรือ U = {x | x เป็นจำนวนเต็ม.}

สมบัติเกี่ยวกับสับเซต

ถ้า A ⊂ B และ B ⊂ A แล้ว A = B
ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C
เซตทุกเซตเป็นสับเซตของตัวเอง คือ ถ้า A เป็นเซตใดๆ แล้ว A ⊂ A
เซตว่างเป็นสับเซตของทุกเซต คือ ถ้า A เป็นเซตใดๆ แล้ว ∅ ⊂ A
ถ้า n(A) = n แล้ว จำนวนสับเซตของเซต A เท่ากับ 2ⁿ สับเซต

พาวเวอร์เซต พาวเวอร์เซตของ A เขียนแทนด้วย P(A) หมายถึง เซตของสับเซตทั้งหมดของ A และจำนวนของสมาชิกของพาวเวอร์เซตหาได้จาก

n(P(A))= 2ⁿ

เช่น กำหนดให้ A = { 1, 2 } จงหาสับเซต และพาวเวอร์เซตของ A

วิธีทำ

สับเซตทั้งหมดของ A คือ ∅, {1}, {2}, {1,2}
ดังนั้น พาวเวอร์เซตของ P(A) = { ∅, {1}, {2}, {1,2} }
n(P(A))= 2ⁿ = 2² = 4

สมบัติเกี่ยวกับพาวเวอร์เซต เมื่อ A, B, X เป็นเซต

X ∈ P(A) ก็ต่อเมื่อ X ⊂ A
A ∈ P(A)
สำหรับทุกเซต A ใดๆ จะได้ว่า ∅ ∈ P(A) และ ∅ ⊂ P(A) ด้วย
P(A) ≠ ∅ สำหรับทุกๆเซต A
P(∅) = {∅}
A ⊂ B ก็ต่อเมื่อ P(A) ⊂ P(B)
ถ้า A เป็นเซตจำกัด ซึ่ง n(A) = n แล้ว n(P(A)) = 2ⁿ
ถ้า A เป็นเซตอนันต์ แล้ว P(A) เป็นเซตอนันต์

เอกภพสัมพัทธ์ คือ เซตที่ประกอบด้วยสมาชิกทั้งหมดของสิ่งที่เราต้องการจะศึกษา สามารถเขียนแทนได้ด้วยสัญลักษณ์ u

เอกภพสัมพัทธ์ (Relative Universe) ในการพูดถึงเรื่องใดก็ตามในแง่ของเซต เรามักมีขอบข่ายในการพิจารณาสมาชิกของเซตที่จะกล่าวถึง โดยมีข้อตกลงว่าเราจะไม่กล่าวถึงสิ่งใดนอกเหนือไปจากสมาชิก ของเซตที่กำหนดขึ้น เช่น ถ้าเรากำหนดเซตของสมาชิกทุกคนในครอบครัวของผู้เรียนเองให้เป็นเซตใหญ่ที่สุด เราจะเรียกเซตนี้ว่า เอกภพสัมพัทธ์ เขียนแทนด้วยสัญลักษณ์ U โดยมีข้อตกลงว่า เมื่อกล่าวถึงสมาชิกของเซตใด ๆ จะไม่กล่าวถึงสิ่งอื่นที่นอกเหนือจากสมาชิกในเอกภพสัมพัทธ์
กำหนดให้ U คือ เซตของจำนวนจริง และ
จะได้ A = {-2,2}
แต่ถ้ากำหนดให้ U คือ เซตของจำนวนเต็มบวก
จะได้ A = {2}
ตัวอย่าง เช่น ถ้าเราจะศึกษาเกี่ยวกับจำนวนเต็ม
U = {…,-2,-1,0,1,2,…}
หรือ U = {x | x เป็นจำนวนเต็ม.}
หมายเหตุ ถ้ากล่าวถึงเซตของจำนวนและไม่ได้กำหนดว่าเซตใดเป็นเอกภพสัมพัทธ์ให้ถือว่าเอกภพสัมพัทธ์คือเซตของจำนวนจริง

ยูเนียน อินเตอร์เซกชันและคอมพลีเมนต์ของเซต

ยูเนียน (Union)
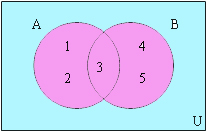
ยูเนียน (Union) มีนิยามว่า เซต A ยูเนียนกับเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ เซต B หรือทั้ง A และ B สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B
ตัวอย่างเช่น
A ={1,2,3}
B= {3,4,5}
∴ A ∪ B = {1,2,3,4,5}
เราสามารถเขียนการยูเนี่ยนลงในแผนภาพได้ดังนี้

อินเตอร์เซกชัน (Intersection)
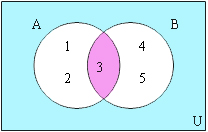
อินเตอร์เซกชัน (Intersection) มีนิยามคือ เซต A อินเตอร์เซกชันเซต B คือ เซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B
ตัวอย่างเช่น
A ={1,2,3}
B = {3,4,5}
∴ A ∩ B = {3}
เราสามารถเขียนการอินเตอร์เซกชันลงในแผนภาพได้ดังนี้

คอมพลีเมนต์ (Complements)
คอมพลีเมนต์ (Complements) มีนิยามคือ ถ้าเซต A ใดๆ ในเอกภพสัมพัทธ์ U แล้วคอมพลีเมนต์ของเซต A คือ เซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่เป็นสมาชิกของ A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A’