ระบบสมการสองตัวแปร

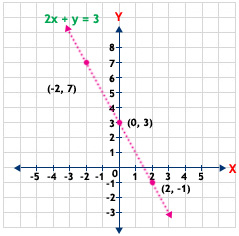
กราฟสมการเชิงเส้นสองตัวแปร

สมการเชิงเส้น คือสมการที่แต่ละพจน์มีเพียงค่าคงตัว หรือเป็นผลคูณระหว่างค่าคงตัวกับตัวแปรยกกำลังหนึ่ง ซึ่งจะมีดีกรีของพหุนามเท่ากับ 0 หรือ 1 สมการเหล่านี้เรียกว่า “เชิงเส้น” เนื่องจากสามารถวาดกราฟของฟังก์ชันบนระบบพิกัดคาร์ทีเซียนได้เป็นเส้นตรง รูปแบบทั่วไปของสมการเชิงเส้นในตัวแปร x และ y คือ

y = ax+b

โดยที่ a คือค่าคงตัวที่แสดงความชันหรือเกรเดียนต์ของเส้นตรง และพจน์ b แสดงจุดที่เส้นตรงนี้ตัดแกน y สำหรับสมการที่มีพจน์ x², y^1/3, xy ฯลฯ ที่มีดีกรีมากกว่าหนึ่งไม่เรียกว่าเป็นสมการเชิงเส้น

รูปแบบทั่วไป

สมการเชิงเส้นที่ซับซ้อน อย่างเช่นตัวอย่างข้างบน สามารถเขียนใหม่โดยใช้กฎเกณฑ์ของพีชคณิตมูลฐานให้อยู่ในรูปแบบที่ง่ายขึ้น ในสิ่งที่จะอธิบายต่อไปนี้ อักษรตัวใหญ่ใช้แทนค่าคงตัว (ที่ไม่ระบุจำนวน) ในขณะที่ x และ y คือตัวแปร

Ax+By+C=0

เมื่อ A กับ B ไม่เป็นศูนย์พร้อมกัน สมการในรูปแบบนี้มักเขียนให้ A ≥ 0 เพื่อความสะดวกในการคำนวณ กราฟของสมการจะเป็นเส้นตรง และทุกๆ เส้นตรงสามารถนำเสนอให้อยู่ในรูปแบบข้างต้นนี้ได้ เมื่อ A ไม่เท่ากับ 0 ระยะตัดแกน x จะอยู่ที่ระยะ −C/A และเมื่อ B ไม่เท่ากับ 0 ระยะตัดแกน y จะอยู่ที่ระยะ −C/B ส่วนความชันของเส้นตรงนี้มีค่าเท่ากับ −A/B
รูปแบบมาตรฐาน

Ax+By=C

เมื่อ A และ B ไม่เป็นศูนย์พร้อมกัน และทั้ง A, B, C จะต้องเป็นจำนวนเต็มที่มีตัวหารร่วมมากเท่ากับ 1 และมักเขียนให้ A ≥ 0 เพื่อความสะดวกเช่นกัน รูปแบบมาตรฐานนี้สามารถแปลงให้เป็นรูปแบบทั่วไปได้ไม่ยากนัก
ข้อสังเกต

1. สมการเชิงเส้นสองตัวแปร เป็นสมการที่มีตัวแปรสองตัวเลขชี้กำลังของตัวแปรแต่ละตัวเป็น1 และไม่มีการคูณกันของตัวแปร
2. คำตอบของสมการเชิงเส้นสองตัวแปร ที่มีx และ y เป็นตัวแปรได้แก่ค่าของ x และ y ที่ทำให้สมการเป็นจริง นิยมเขียนในรูปคู่อันดับ ( x , y ) เช่น (4,8) จะได้ว่า x = 4 , y = 8

**สมการในรูป y = ax b เรียกว่า รูปมาตรฐานของสมการเชิงเส้นสองตัวแปร โดย a เรียกว่าความชันของเส้นตรง ซึ่งค่าของ a และ b จะทำให้ทราบลักษณะกราฟดังนี้คือ

1. ค่าของa บอกให้ทราบว่ากราฟทำมุมอย่างไรกับแกน x ดังนี้
   a > 0 กราฟจะทำมุมแหลมกับแกน x
   a < 0 กราฟจะทำมุมป้านกับแกน x
   a = 0 กราฟจะขนานกับแกน x
2. ค่าของb จะบอกให้ทราบว่ากราฟตัดแกน y ที่จุดใด โดยกราฟจะตัดแกน y ที่ ( 0 , b)
3. ถ้าสมการใด ๆ ที่มีค่าa เท่ากัน จะได้กราฟที่ขนานกัน
4. ถ้าสมการใด ๆ ที่มีค่าa คูณกันได้ –1 จะได้กราฟ 2 เส้นตั้งฉากกัน
5. เนื่องจากกราฟของสมการy = ax b เป็นเส้นตรง ดังนั้นในการเขียนกราฟของสมการดังกล่าวจึงสามารถทำได้โดยการหาจุดเพียง 2 จุด ที่แทน (x, y) แล้วทำให้สมการนั้นเป็นจริง

                โดย จากสมการ y = mx + b เมื่อ m เป็นความชันของเส้นตรง และ b เป็นระยะที่กราฟตัดแกน y เมื่อ x = 0

                เช่น    y = 2x -3

                            ความชันของเส้นตรงคือ 2

                            และกราฟ ตัดแกน y ที่จุด (0,3)

                                        ดังนั้น ความชันของเส้นตรง คือ –A