เซตเบื้อต้นเซต (SET)

เซตเบื้อต้น

ตัวอย่างที่ 1 ก าหนดให้ A เป็นเซตของสระในภาษาอังกฤษนั่นคือ A = {a, e, i, o, u} จะได้ว่า
a ∈ A อ่านว่า a เป็นสมาชิกของเซต A
o ∈ A อ่านว่า o เป็นสมาชิกของเซต A
u ∈ A อ่านว่า u เป็นสมาชิกของเซต A
m ∉ A อ่านว่า m ไม่เป็นสมาชิกของเซต A
y ∉ A อ่านว่า y ไม่เป็นสมาชิกของเซต A
และ n(A) = 5 อ่านว่า จ านวนสมาชิกของเซต A เท่ากับ 5 ตัว

สับเซตคืออะไร

การที่เราจะบอกว่า เซต A เป็นสับเซต(subset)ของเซต B ได้นั้น สมาชิก “ทุกตัวของ A” จะต้องเป็นสมาชิกของ B ด้วย เขียนแทนด้วย A ⊂ B … ตัวอย่างเช่น A = {1,3,5,7} , B = {1,2,3,4,5,6,7,8,9}

เซตว่างเป็นสับเซตของทุกเซต

สับเซต (subset) หรือ “เซตย่อย” คือ เซตที่เล็กกว่าหรือเท่ากันกับเซตที่กำหนด โดยต้องใช้สมาชิกร่วมกับเซตที่กำหนดเท่านั้น

สัญลักษณ์ที่ใช้แทนประโยค “ A เป็นสับเซตของ B” คือ A B และจะเกิดขึ้นได้ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A นั้นเป็นสมาชิกของเซต B ด้วย หรือเมื่อ A เป็นเซตว่างก็ได้

เช่น {1,2}{1,2,3}เนื่องจากทั้ง 1 และ 2 เป็นสมาชิกของ {1,2,3}

รูปแบบ เซต (เล็ก) ⊂ เซต(ใหญ่)

สมบัติของซับเซต

1. A ⊂ A (เซตทุกเซตเป็นสับเซตของตัวมันเอง)

2. A ⊂ U (เซตทุกเซตเป็นสับเซตของเอกภพสัมพัทธ์)

3. Ø ⊂ A (เซตว่างเป็นสับเซตของทุกๆ เซต)

4. ถ้า A ⊂ ø แล้ว A = ø

5. ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C (สมบัติการถ่ายทอด)

6. A = B ก็ต่อเมื่อ A ⊂ B และ B ⊂ A

7. ถ้า A มีจำนวนสมาชิก n ตัว สับเซตของเซตจะมีทั้งสิ้น 2n สับเซต

ตัวอย่าง จงหาสับเซตทั้งหมดของ A เมื่อ A = {2, 4, 6, 8}

A จะมีสับเซตทั้งหมด 2⁴ =16 สับเซต เมื่อแจกแจงสับเซตทั้งหมดจะได้ดังนี้

{2} {4} {6} {8}

{2, 4} {2, 6} {2, 8} {4, 6} {4, 8} {6, 8}

{2, 4, 6} {2, 6, 8} {2, 4, 8} {4, 6, 8}

{2, 4, 6, 8}

ซับเซตและเพาเวอร์เซต ( subset & power set)

สับเซต (Subset) หรือ เซตย่อย

ถ้าสมาชิกทุกตัวของ A เป็นสมาชิกของ B แล้ว จะเรียกว่า A เป็นสับเซตของ B จะเขียนว่า เซต A เป็นสับเซตของเซต B แทนด้วย A ⊂ B

ถ้าสมาชิกบางตัวของ A ไม่เป็นสมาชิกของ B จะเรียกว่า A ไม่เป็นสับเซตของ B เซต A ไม่เป็นสับเซตของเซต B แทนด้วย A ⊄ B

ตัวอย่าง การเป็นสับเซตและไม่เป็นสับเซตกัน

กำหนดให้ A={1,2,3,4,5},B={2,3,5} และ C={2,4}

จะเห็นว่าสมาชิกทุกตัวของ B คือ 2,3 และ 5 เป็นสมาชิกของ A ด้วย ดังนั้น B ⊂ A และสมาชิกของ C คือ 2 และ 4 ก็เป็นสมาชิกของ A ด้วยเช่นกัน ดังนั้น C ⊂ A แต่ในขณะที่สมาชิกของ C ตัวหนึ่ง คือ 4 ไม่เป็นสมาชิกของ B ดังนั้น C ⊄ B

เพิ่มเรื่อง สับเซต หรือ เซตย่อย

การที่เราจะบอกว่า เซต A เป็นสับเซต(subset)ของเซต B ได้นั้น สมาชิก “ทุกตัวของ A” จะต้องเป็นสมาชิกของ B ด้วย เขียนแทนด้วย A ⊂ B

ตัวอย่างเช่น A = {1,3,5,7} , B = {1,2,3,4,5,6,7,8,9}

เราจะสังเกตเห็นว่า สมาชิกทุกตัวของ A เป็นสมาชิกของ B ดังนั้น A เป็นสับเซตของ B (A⊂B) แต่ B ไม่เป็นสับเซตของเซต A (B ⊄ A) เพราะ สมาชิกบางตัวของB ไม่อยู่ใน A

เราอาจจะวาดรูปเพื่อให้เข้าใจมากขึ้น

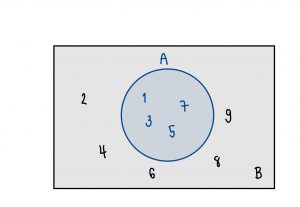
สับเซต หรือ เซตย่อย

จากรูป เราจะเห็นได้ชัดเลยว่า สมาชิกทุกตัวของเซต A อยู่ในเซต B แต่สมาชิกบางตัวของเซต B ไม่อยู่ในเซต A

และเรายังสามารถบอกได้อีกว่า Ø, {1}, {3}, {5}, {7} ⊂ A และ Ø, {1}, {2}, {3} {4}, {5}, {6}, {7}, {8}, {9}⊂ B

สมบัติของพาวเวอร์เซต

∅ ∈ P ( A ) เพราะ ∅ ⊂ A เสมอ
∅ ⊂ P ( A ) เพราะเซตว่างเป็นสับเซตของทุกเซต แล้ว ก็เป็นเซตเช่นกัน
A ∈ P ( A ) เพราะ A ⊂ A เสมอ
ถ้า เป็นเซตจำกัด และ คือจำนวนสมาชิกของ แล้ว จะมีสมาชิก 2 n ( A ) ตัว (เท่ากับจำนวนสับเซตของ )
A ⊂ B ก็ต่อเมื่อ
P ( A ) ∩ P ( B ) = P ( A ∩ B )
P ( A ) ∪ P ( B ) ⊂ P ( A ∪ B )