การแจกจงความน่าจะเป็นของตัวแปรสุ่มชนิดไม่ต่อเนื่อง คือ กฎหรือวิธีการที่กำหนดความน่าจะเป็นให้แก่ค่าตัวแปรสุ่มไม่ต่อเนื่อง โดยการหาค่าความน่าจะเป็นของจุดตัวอย่างต่าง ๆ ที่อยู่ในแซมเปิลสเปซ ที่ให้ค่าเดียวกันกับตัวแปรสุ่มนั้น

Ex. โยนเหรียญ 3 อัน 1 ครั้ง ให้ X แทนจำนวนเหรียญที่ขึ้นหน้าก้อย

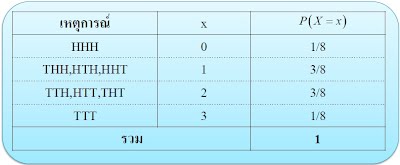
              จะเห็นว่า ค่าที่เป็นไปได้ของ X และความน่าจะเป็นที่ X จะมีค่าต่าง ๆ เรียกว่า การแจกแจงความน่าจะเป็นของตัวแปรสุ่ม X

Ex. ร้านขายของเก่าแห่งหนึ่ง มีแจกันโบราณ 7 ใบ ซึ่งมีตำหนิจำนวน 3 ใบถ้าเสนามาซื้อแจกันโบราณในร้านดังกล่าวจำนวน 3 ใบอย่างสุ่ม จงหาการแจกแจงความน่าจะเป็นของจำนวนแจกันโบราณที่มีตำหนิที่เสนาซื้อมาจากร้านดังกล่าว โดยตาราง, กราฟ, สูตรหรือฟังก์ชัน

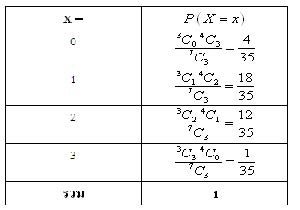
1) หาการแจกแจงความน่าจะเป็น โดยตาราง

      ให้ X แทน จำนวนแจกันโบราณที่มีตำหนิ

                   x = 0,1,2,1

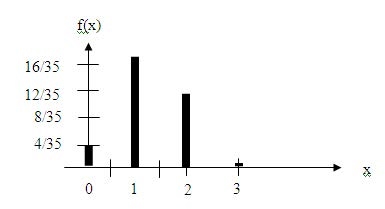
2) หาการแจกแจงความน่าจะเป็น โดยกราฟ

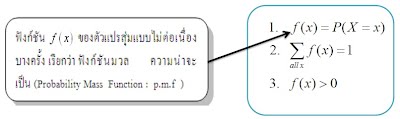
3) หาการแจกแจงความน่าจะเป็น โดยสูตรหรือฟังก์ชัน

การแจกแจงความน่าจะเป็นของตัวแปรสุ่มชนิดไม่ต่อเนื่องที่ส าคัญ (Discrete Probability Distribution)
การทดลองสุ่มแบบทั่วไป หากเราพิจารณาจะพบว่าในบางการทดลองสุ่มนั้น ลักษณะของตัวแปรสุ่ม จะมีลักษณะคล้ายๆ กัน ถึงแม้ว่าจะเป็นการทดลองคนละชนิดกัน เช่น ในการโยนเหรียญ 1 อัน 3 ครั้ง สนใจ จำนวนครั้งที่ขึ้นหัว จำนวนครั้งที่ขึ้นหัวจะมีค่าเป็นไปได้คือ 0,1,2 หรือ 3 และ ในการศึกษาเพศของบุตร โดย สนใจจำนวนบุตรที่เป็นหญิง จากครอบครัวที่มีบุตร 3 คน จะได้ว่าจ านวนบุตรหญิงที่เป็นไปได้คือ 0,1,2 หรือ 3 เช่นเดียวกัน ดังนั้นเราจะเห็นได้ว่า ลักษณะของตัวแปรสุ่มจะมีลักษณะคล้ายๆ กัน จึงตั้งชื่อการแจกแจงความ น่าจะเป็นของการทดลองที่มีลักษณะคล้ายๆ กันนี้ว่าเป็นการแจกแจงความน่าจะเป็นทวินาม (Binomial distribution) และยังมีการแจกแจงของตัวแปรสุ่มชนิดไม่ต่อเนื่องแบบอื่นๆ ที่สำคัญ เช่น การแจกแจงปัวซง (Poisson distribution) เป็นต้น

การทดลองใดๆ ที่ประกอบด้วยการกระทำซ้ าๆ ที่เป็นอิสระกัน และผลที่เกิดขึ้นเป็นไปได้เพียงสองอย่าง คือความสำเร็จ (success) และความไม่สำเร็จ (failure) เช่น การโยนเหรียญหนึ่งอัน 5 ครั้ง เป็นการ
กระทำที่ซ้าๆ กัน 5 ครั้ง ซึ่งแต่ละครั้งเป็นอิสระต่อกัน กล่าวคือ ผลที่ได้จากการโยนเหรียญในแต่ละครั้งไม่ขึ้น ต่อกันและผลจากการโยนเหรียญแต่ละเหรียญจะมีผลเกิดขึ้นได้เพียงสองอย่างคือจะได้หัวหรือได้ก้อยเท่านั้น
ซึ่งหากเราสนใจผลลัพธ์ขึ้นหัว จะถือว่าการขึ้นหัวเป็นความสำเร็จ ส่วนการขึ้นก้อยเป็นความไม่สำเร็จ สำหรับ  ตัวอย่างการโยนเหรียญนี้ความน่าจะเป็นของการขึ้นหัวในแต่ละครั้งเท่ากับ 1/2 และความน่าจะเป็นที่จะขึ้น
ก้อยในแต่ละครั้งเท่ากับ 1/2 เรียกการทดลองแบบนี้ว่าการทดลองทวินาม (binomial experiment)
อีกตัวอย่างหนึ่ง เช่น การหยิบไพ่จากส ารับครั้งละหนึ่งใบ 3 ครั้ง โดยการหยิบครั้งแรกแล้วใส่คืนก่อน การหยิบครั้งต่อไป ถ้าก าหนดให้การหยิบไพ่ได้ไพ่สีแดงเป็นความส าเร็จ และการหยิบไพ่ได้ไพ่สีดำเป็นความไม่
สำเร็จ ในแต่ละครั้งความน่าจะเป็นที่หยิบได้ไพ่สีแดงหรือความส าเร็จมีค่าเท่ากับ ½ และความน่าจะเป็นที่หยิบ
ไพ่ได้สีดำ หรือความไม่ส าเร็จเท่ากับ ½ จะเห็นว่าเป็นการทดลองซ้ าๆกัน 3 ครั้ง ที่เป็นอิสระกัน การกระทำแต่ละครั้งมีผลเกิดขึ้นได้สองอย่าง และความน่าจะเป็นของความส าเร็จในแต่ละครั้งมีค่าเท่ากัน การทดลองนี้จึง
เรียกว่า การทดลองแบบทวินาม เช่นเดียวกัน ดังนั้นเราอาจสรุปได้ว่า การทดลองแบบทวินามมีลักษณะทั่วๆ ไปดังนี้
1. การทดลองประกอบไปด้วยการกระท าซ้ าๆ กัน n ครั้ง
2. ในการกระทำแต่ละครั้งจะมีผลลัพธ์เกิดขึ้นได้2 อย่าง คือ ความส าเร็จ และ ความไม่สำเร็จ
3. ความน่าจะเป็นของความส าเร็จ ที่เกิดขึ้นจากการกระท าแต่ละครั้งมีค่าคงที่เท่ากับ p และความ
น่าจะเป็นของความไม่สำเร็จเท่ากับ q = 1 – p
4. การกระทำแต่ละครั้งเป็นอิสระต่อกัน