สมบัติของเซตและสับเซตที่น่าสนใจ

สมบัติของเซตที่น่าสนใจ

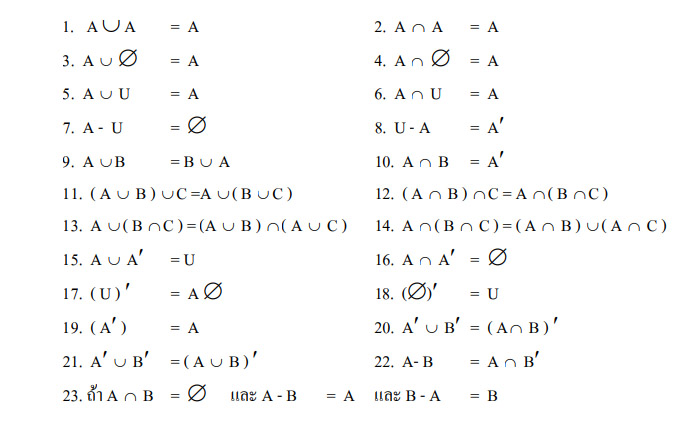
นิยามของเซต เซต คือ คำที่ใช้บ่งบอกกลุ่มของสิ่งต่าง ๆ ทำให้ทราบว่าเมื่อพูดถึงกลุ่มใดแล้วก็จะทราบได้อย่างแน่นอนว่าสิ่งใดอยู่ในกลุ่ม และสิ่งใดไม่อยู่ในกลุ่ม โดยจะเรียกสิ่งที่อยู่ในเซตว่า สมาชิกของเซต เช่น

เซตของอักษรสระในภาษาอังกฤษ หมายถึง กลุ่มของอักษร a, e, i, o, และ u

• จำนวนสมาชิกเซต A เขียนแทนด้วย n(A)
• a เป็นสมาชิกของเซต A เขียนแทนด้วย a ∈ A
• b ไม่เป็นสมาชิกของเซต A เขียนแทนด้วย b ∉ A

**สมบัติของสับเซตที่น่าสนใจ

A ⊂ A (เซตทุกเซตเป็นสับเซตของตัวมันเอง)

A ⊂ U (เซตทุกเซตเป็นสับเซตของเอกภพสัมพัทธ์)

ø ⊂ A (เซตว่างเป็นสับเซตของทุกๆ เซต)

ถ้า A ⊂ ø แล้ว A = ø

ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C (สมบัติการถ่ายทอด)

A = B ก็ต่อเมื่อ A ⊂ B และ B ⊂ A

ถ้า A มีจำนวนสมาชิก n ตัว สับเซตของเซตจะมีทั้งสิ้น 2n สับเซต

**สมบัติของสับเซตอื่นๆ

พาเวอร์เซต (Power Set)

คำว่า เพาเวอร์เซต เป็นคำศัพท์เฉพาะ ซึ่งใช้เป็นชื่อเรียกเซตเซตหนึ่งที่เกี่ยวข้องกับเรื่องสับเซต

เพาเวอร์เซตของ A เขียนแทนด้วย P(A)

P(A) คือเซตที่มีสับเซตทั้งหมดของ A เป็นสมาชิก

สมบัติของเพาเวอร์เซต

ให้ A , B เป็นเซตใดๆ

1) ø ⊂ P(A)

2) A ⊂ P(A)

3) P(A) ≠ ø

4) P(A) ⊂ P(B) ก็ต่อเมื่อ A ⊂ B

5) ถ้า A มีสมาชิก n ตัว P(A) จะมีสมาชิก 2ⁿ ตัว

สมบัติของสับเซต

1) A ⊂ A (เซตทุกเซตเป็นสับเซตของตัวมันเอง)

2) A ⊂ U (เซตทุกเซตเป็นสับเซตของเอกภพสัมพัทธ์)

3) ø ⊂ A (เซตว่างเป็นสับเซตของทุกๆ เซต)

4) ถ้า A ⊂ ø แล้ว A = ø

5) ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C (สมบัติการถ่ายทอด)

6) A = B ก็ต่อเมื่อ A ⊂ B และ B ⊂ A

7) ถ้า A มีจำนวนสมาชิก n ตัว สับเซตของเซตจะมีทั้งสิ้น 2ⁿ สับเซต

สับเซตแท้

นิยาม A เป็นสับเซตแท้ของ B ก็ต่อเมื่อ A⊂B และ A ≠ B

ตัวอย่าง กำหนดให้ A = { a , b , c } จงหาสับเซตแท้ทั้งหมดของ A

วิธีทำ สับเซตแท้ของ A ได้แก่

ø, {a} , {b} ,{c} , {a,b} , {a ,c} , {b,c}