ตรรกศาสตร์ ม.4
- ประพจน์
- การเชื่อมประพจน์
- ค่าความจริงของประพจน์
- การสมมูลและนิเสธของประพจน์
- สัจนิรันดร์และการอ้างเหตุผล
- ตัวบ่งปริมาณและประโยคเปิด
ประพจน์
คือ ประโยคที่บอกค่าความจริง (truth value)ได้
ว่าเป็นจริง (true) หรือ เท็จ(False) เพียงอย่างใดอย่าง หนึ่งเท่านั้น บอกเล่า หรือประโยคปฏิเสธก็ได้
ตัวอย่างประโยคที่ไม่เป็นประพจน์
1. ประโยคค าถาม เช่น ใครกันนะ
2. ประโยคค าสั่ง เช่น จงนั่งลง
3. ประโยคขอร้อง เช่น ช่วยปิ ดหน้าต่างให้หน่อย
4. ประโยคอ้อนวอน เช่น โปรดเมตตาด้วยเถิด
5. ประโยคแสดงความปรารถนา เช่น ฉันอยากเป็นนก
6. ประโยคเปิด เช่น เขาเป็นดารานักร้อง
การเชื่อมประพจน์
โดยปกติเมื่อกล่าวถึงข้อความหรือประโยคนั้นมักจะมีกริยามากกว่าหนึ่งตัว แสดงว่าได้นำประโยคมาเชื่อมกัน มากกว่าหนึ่งประโยค ดังนั้นถ้านำประพจน์มาเชื่อมกัน ก็จะได้ประพจน์ใหม่ ซึ่งสามารถบอกได้ว่าเป็นจริงหรือเป็นเท็จ ตัวเชื่อมประพจน์มีอยู่ 5 ตัว และตัวเชื่อมที่ใช้กันมากในตรรกศาสตร์คือ และ หรือ ถ้า…แล้ว ก็ต่อเมื่อ ไม่
- ตัวเชื่อมประพจน์ “และ”
การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “และ” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ∧ q ซึ่งจะมีค่าความจริงเป็นจริง (T) เมื่อ p และ q มีค่าความจริงเป็นจริง (T) ทั้งคู่ นอกนั้นมีค่าความจริงเป็นเท็จ (F) - ตัวเชื่อมประพจน์ “หรือ”
การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “หรือ” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ∨q ซึ่งจะมีค่าความจริงเป็นเท็จ (F) เมื่อ p และ q มีค่าความจริงเป็นเท็จ (F) ทั้งคู่ นอกนั้นมีค่าความจริงเป็นจริง (T) - ตัวเชื่อมประพจน์ “ถ้า…แล้ว”
การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “ถ้า…แล้ว” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p → q ซึ่งจะมีค่าความจริงเป็นเท็จ (F) เมื่อ p เป็นจริง (T) และ q เป็นเท็จ (F) นอกนั้นมีค่าความจริงเป็นจริง (T) - ตัวเชื่อมประพจน์ “ก็ต่อเมื่อ”
การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “ก็ต่อเมื่อ” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ⇔ q ซึ่งจะมีค่าความจริงเป็นจริง (T) เมื่อ p และ q มีค่าความจริงตรงกัน และจะมีค่าความจริงเป็นเท็จ (F) เมื่อ p และ q มีค่าความจริงตรงข้ามกัน - นิเสธของประพจน์ “ไม่”
นิเสธของประพจน์ใดๆ คือ ประพจน์ที่มีค่าความจริงตรงกันข้ามกับประพจน์นั้นๆ และสามารถเขียนแทนนิเสธของ p ได้ด้วย ~p
ประโยคนิเสธ (Negations)
คือ ประโยคที่แสดงค่าความจริงตรง
ข้ามกับประโยคเดิม
สัญลักษณ์ทั่วไป คือ ~
~ P แทนนิเสธของประโยค P
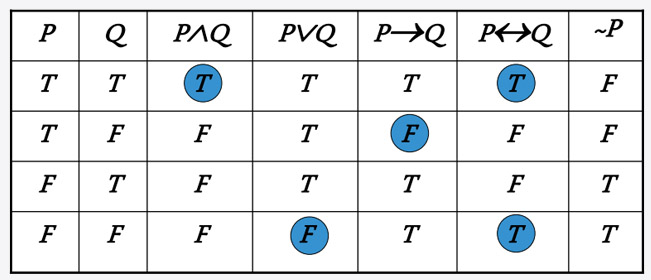
ตัวอย่างประพจน์ที่เป็นนิเสธกันที่ควรทราบ มีดังนี้
~(p ∧ q) สมมูลกับ ~p ∨ ~q
~(p ∨ q) สมมูลกับ ~p ∧ ~q
~(p → q) สมมูลกับ p ∧ ~q
~(p ⇔ q) สมมูลกับ (p ⇔ ~q) ∨(q ⇔ ~p)
~(p ⇔ q) สมมูลกับ (p ∧ ~q) ∨ ( q ∧~p)
การเชื่อมประพจน์ มีด้วยกัน 4 แบบ ได้แก่
- และ (∧) เป็นจริงเพียงกรณีเดียวคือ T ∧ T เป็น T
- หรือ (∨) เป็นเท็จเพียงกรณีเดียวคือ F ∨ F เป็น F
- ถ้า…แล้ว (→) เป็นเท็จเพียงกรณีเดียวคือ T → F เป็น F
- ก็ต่อเมื่อ (↔) ถ้ามีค่าความจริงเหมือนกันจะเป็นจริง ไม่เหมือนกันจะเป็นเท็จ
หรือดังตารางต่อไปนี้
| p | q | p∧q | p∨q | p→q | p↔q |
| T | T | T | T | T | T |
| T | F | F | T | F | F |
| F | T | F | T | T | F |
| F | F | F | F | T | T |
ตรวจสอบสัจนิรันดร์ โดย การสร้างตารางค่าความจริง
ประพจน์ (p∨q)∧p(p∨q)∧p เป็นสัจนิรันดร์หรือไม่
จากประพจน์ที่กำหนดให้ จะมีประพจน์ย่อยทั้งหมดสองประพจน์ ดังนั้นสร้างตารางที่มีประพจน์สองประพจน์นี้ขึ้นมา
สัจนิรันดร์และการอ้างเหตุผล
การอ้างเหตุผล
การอ้างเหตุผลคือ การอ้างว่า เมื่อมีประพจน์ p1,p2,…pn, ชุดหนึ่ง แล้วสามารถสรุปประพจน์ C ประพจน์หนึ่งได้ การอ้างเหตุผลประกอบด้วยส่วนสำคัญสองส่วนคือ เหตุหรือสิ่งที่กำหนดให้ ได้แก่ ประพจน์ p1,p2,…pn, และ ผลหรือข้อสรุป คือ ประพจน์ C โดยใช้ตัวเชื่อม ∧ เชื่อมเหตุทั้งหมด เข้าด้วยกัน และใช้ตัวเชื่อม → เชื่อมส่วนที่เป็นเหตุกับผลดังนี้
(p1 ∧ p2 ∧ … ∧ pn,) → C
จะกล่าวว่า การอ้างเหตุผลนี้ สมเหตุสมผล (valid) ถ้ารูปแบบของประพจน์ (p1 ∧ p2 ∧ … ∧ pn,) → C เป็นสัจนิรันดร์ และจะกล่าวว่า การอ้างเหตุผลนี้ ไม่สมเหตุสมผล (invalid) ถ้ารูปแบบของประพจน์ (p1 ∧ p2 ∧ … ∧ pn,) → C ไม่เป็นสัจนิรันดร์ ดังนั้น ในการตรวจสอบความสมเหตุสมผลจึงใช้วิธีเดียว กับการตรวจสอบสัจนิรันดร์
ตัวอย่าง
กำหนดให้ p และ q เป็นประพจน์ จงพิจารณาว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่
เหตุ
- p→q
- p
ผล q
วิธีทำ ขั้นที่ 1 ใช้ ∧ เชื่อมเหตุเข้าด้วยกัน และใช้ → เชื่อมส่วนที่เป็นเหตุกับผล จะได้รูปแบบของประพจน์คือ [(p → q) ∧ p]→q
ขั้นที่ 2ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่ สมมติให้[(p → q) ∧ p]→q เป็นเท็จ

จากแผนภาพ แสดงว่า รูปแบบของประพจน์ [(p → q) ∧ p]→q เป็นสัจนิรันดร์
ดังนั้น การอ้างเหตุผลนี้สมเหตุสมผล
ตัวอย่าง
กำหนดให้ p และ q เป็นประพจน์ จงพิจารณาว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่
เหตุ
- p→q
- ∼p
ผล ∼q
วิธีทำ ขั้นที่ 1 ใช้ ∧ เชื่อมเหตุเข้าด้วยกัน และใช้ → เชื่อมส่วนที่เป็นเหตุกับผล จะได้รูปแบบของประพจน์คือ [(p → q) ∧ ∼p]→∼q
ขั้นที่ 2ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่ สมมติให้[(p → q) ∧ ∼p]→∼q เป็นเท็จ

จากแผนภาพ มีกรณีที่ p เป็นเท็จ และ q เป็นจริง ที่ทำให้ [(p → q) ∧ ∼p]→∼q เป็นเท็จ
แสดงว่า รูปแบบของประพจน์ [(p → q) ∧ ∼p]→∼q ไม่เป็นสัจนิรันดร์
ดังนั้น การอ้างเหตุผลนี้ไม่สมเหตุสมผล
ตัวอย่าง
จงพิจารณาว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่
เหตุ
- ถ้าฝนตกที่บ้านของสุชาดา แล้วหลังคาบ้านของสุชาดาเปียก
- หลังคาบ้านของสุชาดาไม่เปียก
ผล ฝนไม่ตกที่บ้านของสุชาดา
วิธีทำ ให้ p แทนประพจน์ “ฝนตกที่บ้านของสุชาดา”
q แทนประพจน์ “หลังคาบ้านของสุชาดาเปียก”
เขียนแทนข้อความข้างต้นในรูปสัญลักษณ์ได้ดังนี้
เหตุ
- p→q
- ∼q
ผล ∼p
ดังนั้น รูปแบบของประพจน์ในการอ้างเหตุผลนี้ คือ[(p → q) ∧ ∼q]→∼p
ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่
สมมติให้ [(p → q) ∧ ∼q]→∼p เป็นเท็จ

จากแผนภาพ แสดงว่า รูปแบบของประพจน์ [(p → q) ∧ ∼q]→∼p เป็นสัจนิรันดร์
ดังนั้น การอ้างเหตุผลนี้สมเหตุสมผล
ตัวอย่าง
จงพิจารณาว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่
เหตุ
- ถ้าแป้งได้โบนัส แล้วแป้งจะฝากเงินกับธนาคาร 10,000 บาท
- แป้งฝากเงินกับธนาคาร 10,000 บาท
ผล แป้งได้โบนัส
วิธีทำ ให้ p แทนประพจน์ “แป้งได้โบนัส”
q แทนประพจน์ “แป้งฝากเงินกับธนาคาร 10,000 บาท”
เขียนแทนข้อความข้างต้นในรูปสัญลักษณ์ได้ดังนี้
เหตุ
- p→q
- q
ผล p
ดังนั้น รูปแบบของประพจน์ในการอ้างเหตุผลนี้ คือ[(p → q) ∧ q]→p
ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่
สมมติให้ [(p → q) ∧ q]→ p เป็นเท็จ
ประโยคเปิดและตัวบ่งปริมาณ(Logical Quantifier)-ตรรกศาสตร์
ประโยคเปิด
ประโยคเปิด คือประโยคบอกเล่าหรือปฏิเสธที่มีตัวแปร ประโยคเปิดไม่สามารถบอกค่าความจริงได้ แต่ถ้าแทนค่าตัวแปรลงไป ประโยคเปิดจะกลายเป็นประพจน์ กล่าวคือสามารถบอกค่าความจริงได้
ตัวอย่างของประโยคเปิด
x+10=15
เป็นประโยคเปิด เพราะเราไม่ทราบว่า x มีค่าเท่าไร จึงไม่สามารถบอกได้ว่าประโยคนี้เป็นจริงหรือเท็จ
หากแทนค่า x ด้วย 5 เราสามารถบอกได้ว่าประโยคนี้เป็นจริง ซึ่ง 5+10=15 เป็นประพจน์
หรือหากแทนค่า x ด้วย 1 เราสามารถบอกได้ว่าประโยคนี้เป็นเท็จ ซึ่ง 1+10=15 ก็ถือว่าเป็นประพจน์เช่นกัน
คือ ประโยคบอกเล่าหรือประโยคปฏิเสธที่มีตัวแปรไม่เป็นประพจน์และเมื่อแทนที่ตัวแปร ด้วยสมาชิกในเอกภพสัมพัทธ์แล้วได้ประพจน์ บทนิยาม ประโยคเปิดคือ ประโยคบอกเล่า ซึ่งประกอบด้วยตัวแปรหนึ่งตัวหรือมากกว่าโดยไม่เป็นประพจน์ แต่จะเป็นประพจน์ได้ เมื่อแทนตัวแปรด้วยสมาชิกเอกภพสัมพัทธ์ตามที่กำหนดให้
นั่นคือเมื่อแทนตัวแปรแล้วจะสามารถบอกค่าความจริง
ประโยคเปิด เช่น
1. เขาเป็นนักว่ายน้ำทีมชาติไทย
2. x – 6 = 10
3. y < – 6
ประโยคที่ไม่ใช่ประโยคเปิด เช่น
1. 10 เป็นคำตอบของสมการ x – 1 = 7
2. โลกหมุนรอบตัวเอง
3. จงหาค่า x จากสมการ 2x + 1 = 8
4. กรุณานั่งเงียบ ๆ
5. ห้ามสูบบุหรี่
ข้อตกลง
1. นิยมแทนประพจน์ด้วย p,q,r,s,…
2. นิยมแทนประโยคเปิดด้วย P(x) , Q(x) ,… P(x,y) , Q(x, y), … โดย P(x) , Q(x) , … แทน ประโยคเปิดที่มี x เป็นตัวแปร โดย P(x, y) , Q(x, y) , … แทน ประโยคเปิดที่มี x และ yเป็นตัวแปร
3. ค่าความจริงที่เป็น ” จริง ” จะเขียนแทนด้วย ” T ”
4. ค่าความจริงที่เป็น” เท็จ” จะเขียนแทนด้วย ” F ”
• เขาเป็นคนดี ⇒ เป็นประโยคเปิดที่ประกอบด้วยตัวแปร “เขา”
• x > 3 ⇒ เป็นประโยคเปิดที่ประกอบด้วยตัวแปร “x” Share this:
ประโยคเปิด และ ตัวบ่งปริมาณ
ประโยคเปิด
ประโยคเปิด คือ ประโยคบอกเล่าหรือปฏิเสธที่มีตัวแปร โดยเมื่อแทนค่าตัวแปรด้วยสมาชิกใน
เอกภพสัมพัทธ์ ประโยคเปิดจะกลายเป็นประพจน์
สัญลักษณ์
ประโยคเปิดที่มี x เป็นตัวแปร ใช้สัญลักษณ์ P(x), Q(x),…
***ประโยคเปิด ใช้ตั้วเชื่อมต่างๆ (∧,∨,→,↔) และ นิเสธ (∼) ได้เหมือนกับที่ใช้กับประพจน์
ตัวบ่งปริมาณ 1 ตัว
กำหนดให้ U คือ เอกภพสัมพัทธ์
∀x[P(x)] หมายถึง สมาชิกทุกตัว (แต่ละตัว) ในเอกภพสัมพัทธ์
แทนค่าใน x ของประโยคเปดิ P(x)
∃x[P(x)] หมายถึง สมาชิกอย่างน้อย 1 ตัว ในเอกภพสัมพัทธ์
แทนค่าใน x ของประโยคเปดิ P(x)
∀x[P(x)] มีค่าความจริงเป็นจริง
เมื่อ สมาชิกทุกตัว(แต่ละตัว)ในเอกภพสัมพัทธ์แทนค่าใน P(x) แล้วเป็นจริง
∀x[P(x)] มีค่าความจริงเป็นเท็จ
เมื่อ มีสมาชิกอย่างน้อย 1 ตัวในเอกภพสัมพัทธ์แทนค่าใน P(x) แล้วเป็นเท็จ
∃x[P(x)] มีค่าความจริงเป็นจริง
เมื่อ มีสมาชิกอย่างน้อย 1 ตัวในเอกภพสัมพัทธ์แทนค่าใน P(x) แล้วเป็นจริง
∃x[P(x)] มีค่าความจริงเป็นเท็จ
เมื่อ ไม่มีสมาชิกตัวใดเลยในเอกภพสัมพัทธที่แทนค่าใน P(x) แล้วเป็นจริง
สูตรนี้ออกสอบบ่อยมาก!!!
∼ ∀x[P(x)] ≡ ∃x[∼ P(x)]
∼ ∃x[P(x)] ≡ ∀x[∼ P(x)]
รู้ไว้นะ!!!
กำหนดให้ P(x) คือ 3x ≥ 2 จะได้ ∼ P(x) คือ 3x < 2
ตัวบ่งปริมาณ 2 ตัว
กำหนดให้ U คือ เอกภพสัมพัทธ์
มีทั้งหมด 8 แบบ
1) ∀x∀y[P(x, y)]เป็น จริง
เมื่อ นำแต่ละตัวใน U แทนใน x แล้วสามารถนำทุกตัวใน U แทนใน y แล้วเป็นจริง
2)∀x∃y[P(x, y)]เป็น จริง
เมื่อ นำแต่ละตัวใน U แทนใน x แล้วสามารถนำอย่างน้อย 1 ตัวใน U แทนใน y แล้วเป็นจริง
3)∃ x∀y[P(x, y)]เป็น จริง
เมื่อ นำอย่างน้อย 1 ตัวใน U แทนใน x แล้วสามารถนำทุกตัวใน U แทนใน y แล้วเป็นจริง
4)∃ x∃y[P(x, y)] เป็น จริง
เมื่อ นำอย่างน้อย 1 ตัวใน U แทนใน x แล้วสามารถนำอย่างน้อย 1 ตัวใน U แทนใน y แล้วเป็นจริง
5) ∀y∀x[P(x, y)]เป็น จริง
เมื่อ นำแต่ละตัวใน U แทนใน y แล้วสามารถนำทุกตัวใน U แทนใน x แล้วเป็นจริง
6)∀ y∃x[P(x, y)]เป็น จริง
เมื่อ นำแต่ละตัวใน U แทนใน y แล้วสามารถนำอย่างน้อย 1 ตัวใน U แทนใน x แล้วเป็นจริง
7) ∃y∀x[P(x, y)]เป็น จริง
เมื่อ นำอย่างน้อย 1 ตัวใน U แทนใน y แล้วสามารถนำทุกตัวใน U แทนใน x แล้วเป็นจริง
8)∃y∃x[P(x, y)]เป็น จริง
เมื่อ นำอย่างน้อย 1 ตัวใน U แทนใน y แล้วสามารถนำอย่างน้อย 1 ตัวใน U แทนใน x แล้วเป็นจริง
สูตรนี้ออกสอบบ่อยมาก!!!
∼ ∀x∀y[P(x, y)] ≡ ∃x∃y[∼ P(x, y)]
∼ ∃x∃y[P(x, y)] ≡ ∀x∀y[∼ P(x, y)]
∼ ∀x∃y[P(x, y)] ≡ ∃x∀y[∼ P(x, y)]
∼ ∃x∀y[P(x, y)] ≡ ∀x∃y[∼ P(x, y)]






