กราฟแบบออยเลอร์
อยเลอร์ได้ให้ทฤษฎีที่เกี่ยวกับปัญหานี้ไว้ดังนี้
-
- เครือข่าย ที่แสดงเป็นกราฟจะประกอบด้วยจุดเชื่อมโยง (Vertices) และเส้นเชื่อมโยงระหว่างจุด เรียกว่า arcs
- จุด ที่มีจำนวนเส้นที่เชื่อมออกไปยังจุดอื่นเป็นจำนวนคี่ เรียกว่า odd และถ้าจุดนั้นมีเส้นเชื่อมออกไปยังจุดอื่นเป็นจำนวนคู่ จะเรียกว่า even
- เส้นทางออยเลอร์ คือเส้นทางที่ลากผ่านเส้นต่าง ๆ ในเครือข่าย โดยแต่ละเส้นลากผ่านได้เพียงครั้งเดียว
- ทฤษฎีของออยเลอร์ กล่าวว่า ถ้าหากว่าเครือข่ายใดมีจุดที่เป็น odd มากกว่าสองขึ้นไป จะไม่มีทางสร้างเส้นทางออยเลอร์ได้
- เครือข่าย ที่แสดงเป็นกราฟจะประกอบด้วยจุดเชื่อมโยง (Vertices) และเส้นเชื่อมโยงระหว่างจุด เรียกว่า arcs
ความเป็นมาของทฤษฎีกราฟ เกิดจากปัญหาของการต้องการเดินท่องเทียวให้ทัวเมืองโคนิกสเบอร์ก ซึงเลออนฮาร์ด ออยเลอร์ คิดว่าเป็นไปไม่ได้ทีจะเดิน
ข้ามสะพานดังกล่าวโดยไม่ซําและให้ทัวเมืองได้ นันคือ ปัญหานีต้องการคําตอบว่ากราฟ ของเมืองโคนิกสเบอร์ก ต้องมีรอยเดิน (หรือวงจร) ซึงรวมเส้นเชือม ทังหมดในกราฟหรือไม่
ดังนัน ออยเลอร์ จึงหาวิธีตอนปัญหานีโดยใช้กราฟมาช่วยในการ พิสูจน์ดังต่อไปนี้
ทฤษฎีบท
กราฟ G ของปัญหาสะพานโคนิกเบอร์ก ไม่รอยเดินทีประกอบด้วย
เส้นทังหมด
QRSP
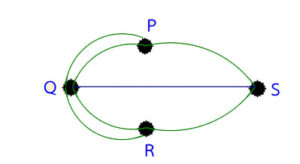
พิสูจน์
(โดยการขัดแย้ง) ถ้ากราฟ G มีรอยเดิน P ซึงรวมทกเส้นใน
กราฟ รอยเดิน P จะต้องเริมต้นทีจดยอดใดจดยอด
หนึง คือ จด Q หรือ R หรือ P หรือ S
จดเริมต้นและจดสินสด
ถ้าให้จดยอด
v เป็นจดในกล่ม Q , R , P ซึงไม่เป็นจดเริมต้นหรือจดสินสด
เนื่องจากจดยอด
Q , R , P มีดีกรีเท่ากับ 3 หรือ 5
ดังนัน เมือมีรอยเดินของ P เข้ามาทีจดุ v จะต้องมีรอยเดินของ P ออกจาก v จึงเหลือเส้นเชือมของ v หนึงเส้น ทีรอยเดิน P จะต้องผ่าน เพราะยังไม่ได้ใช้ แต่เมือ
ใช้เส้นเชือมทีเข้ามาที P จะไม่มีเส้นเชือมออกจาก v
ลองพิจารณาจากปัญหากราฟต่อไปนี้
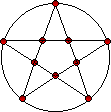
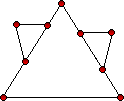
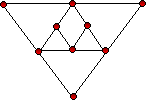
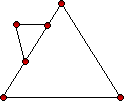
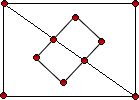
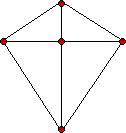
เฉลยปัญหาทฤษฎีกราฟของออยเลอร์

มีเส้นทางออยเลอร์

ไม่มีเส้นทางออยเลอร์ เพราะมีจุดที่มีจำนวนเส้นเชื่อมออกไปยังจุดอื่นเป็นจำนวนคี่ มากกว่า 2 จุด (4 จุด)

มีเส้นทางออยเลอร์

มีเส้นทางออยเลอร์

ไม่มีเส้นทางออยเลอร์ เพราะมีจุดที่มีจำนวนเส้นเชื่อมออกไปยังจุดอื่นเป็นจำนวนคี่ มากกว่า 2 จุด

มีเส้นทางออยเลอร์
ที่มา : รศ. ยืน ภู่วรวรรณ, สำนักบริการคอมพิวเตอร์ มหาวิทยาลัยเกษตรศาสตร์






