กราฟแบบแฮมิลตัน
บทที่6 กราฟแบบแฮมิลตัน
แฮมิลตันได้ริเริ่มการคิดว่าจะเดินทางอย่างไรให้ผ่านเมืองสําคัญแต่ละแห่งเพียง ครั้งเดียวแล้วกลับมายังที่เดิมได้
บทนิยาม
กราฟหรือทุกกราฟ G ซึ่งมีวงเยียนที่รวมทุกจุดใน G เรียกว่าเป็น
กราฟแบบแฮมิลตัน ส่วนวิถีซึ่งรวมทุกจุดใน G เรียกว่า วิถีแบบแฮมิลตัน
กราฟแฮมิลตัน
วงที่เป็นกราฟย่อยแผ่ทัวของกราฟได้เริ่มศึกษาโดย โทมัส พี เคิร์กแมน (Thomas P. Kirkman) ในปี พ.ศ. 2398 แต่ได้รับการตัAงชือตาม เซอร์ วิลเลียม แฮมิลตัน (William Hamilton) โดยแฮมิลตันได้ศึกษา
เกี่ยวกับเกมที่เล่นกับทรงสิบสองหน้า (dodecahedron) โดยมีจุดยอดยี่สิบจุดบนทรงเหลี่ยมแทนเมืองสําคัญของโลกยีสิบเมือง จุดประสงค์ของเกมคือการหาเส้นทางผ่านจุดยอดทุกจุดไปตามขอบของทรงเหลี่ยมโดยเมื่อ
ผ่านทุกเมืองเมืองละหนึ่งครัAงแล้วสามารถกลับมาที่จุดตัAงต้นได้ทันที แฮมิลตันได้จําลองทรงเหลี่ยมนี A ในรูปของ
กราฟ (ดูตัวอย่าง 4.2.2) และหาวงทีเป็นกราฟย่อยแผ่ทั่วของกราฟซึ่งก็คือคําตอบของเกมนั้นเอง
วงแฮมิลตัน (Hamiltonian cycle) ของกราฟ G คือ วงที่มีจุดยอดของ G ทุกจุด
วิถีแฮมิลตัน (Hamiltonian path) ของกราฟ G คือ วิถีที่มีจุดยอดของ G ทุกจุด
กราฟแฮมิลตัน (Hamiltonian graph) คือ กราฟที่มีวงแฮมิลตัน
ข้อสังเกต
การลบเส้นใด ๆ ออกจากวงเวียนแบบแฮมิลตันจะทําให้ได้วิถีแบบแฮมิลตัน
ดังนั้น กราฟอาจมีวิถีแบบแฮมิลตัน แต่ไม่มีวงเวียนแบบแฮมิลตัน
ตัวอย่าง จงพิจารณากราฟต่อไปนี้
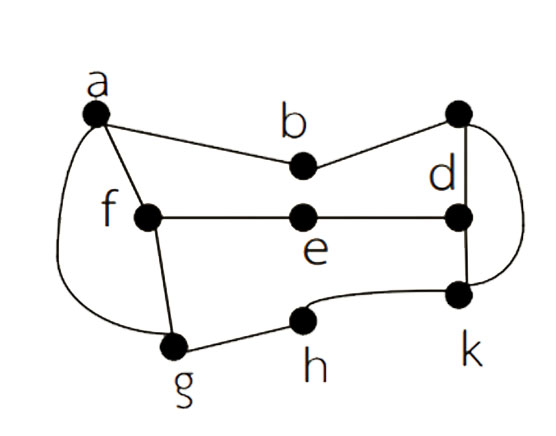
จะเห็่นว่ากราฟมีวิถีแบบแฮมิลตัน คือ a b c d e f g h k
แต่กราฟไม่มีวงเวียนแบบแฮมิลตัน
ตัวอย่าง จงพิจารณากราฟต่อไปนี้
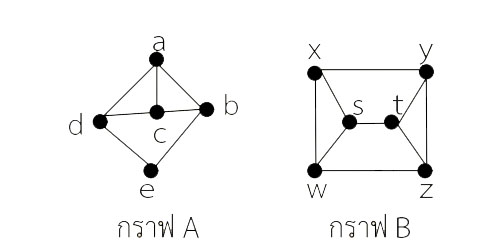
จะเห็นว่า กราฟ A มีวงเวียนแบบแฮมิลตัน คือ a b e d c a
กราฟ B มีวงเวียนแบบแฮมิลตัน คือ x y z t s w x