สรุปเนื้อหาเรื่องฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม
ฟังก์ชันเอกซ์โพเนนเชียล คืออะไร..
ฟังก์ชันเอกซ์โพเนนเชียล คือ ฟังก์ชันที่เขียนอยู่ในรูป {(x, y) ∈ ×
: y = ax } โดยที่ a เป็นจำนวนจริงที่มากกว่า 0 และ a ≠ 1 เช่น 2x , 1.2x, 3-x , 1.5-xซึ่งพูดอีกอย่างก็คือ จำนวนจริงที่มีเลขชี้กำลังเป็นตัวแปรนั่นเอง
ฟังก์ชันเอกซ์โพเนนเชียล คือ f = { (x, y) ∈ R × R+ / y = ax , a > 0, a ≠ 1 }
ฟังก์ชันเพิ่มและฟังก์ชันลด
f เป็นฟังก์ชันเพิ่ม เมื่อ
a > 1
เมื่อ a มากกว่า 1 และเมื่อ x เพิ่มขึ้นเรื่อยๆ จะทำให้ ค่าของ f เพิ่มขึ้นเรื่อยๆ ทำให้ f เป็นฟังก์ชันเพิ่ม
f เป็นฟังก์ชันลด เมื่อ
0 < a < 1
เมื่อ a อยู่ระหว่าง 0 กับ 1 เช่น 0.5, 0.3 เมื่อ x เพิ่มขึ้นเรื่อยๆ ค่าของ f จะลดลงเรื่อยๆ ทำให้ f เป็นฟังก์ชันลด
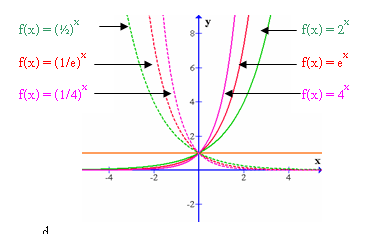
เมื่อ a > 1 ค่า a ยิ่งมากขึ้นกราฟจะยิ่งชัน
เมื่อ 0 < a < 1 ค่า a ยิ่งน้อย กราฟจะยิ่งชัน
นิยามของฟังก์ชันเอกซ์โพเนนเชียล
ฟังก์ชันเอกซ์โพเนนเชียล (Exponential Function)
จากการศึกษาในเรื่องเลขยกกำลัง ซึ่งท้ายที่สุดเราได้สนใจเลขยกกำลังที่มีฐานเป็นจำนวนจริงบวก และเลขชี้กำลังเป็นจำนวนจริงใด ๆ
แต่ได้มีนักคณิตศาสตร์ได้สังเกตเห็นว่า ถ้าเลขยกกำลังมีฐานเป็น 1 และเลขชี้กำลังเป็นจำนวนจริงใด ๆ ดังนี้
ถ้ากำหนดให้ a = 1 และ x เป็นจำนวนจริงใดแล้วจะได้
ax = 1x = 1
ข้อสังเกต
- ไม่ว่า x จะเป็นจำนวนจริงใด ๆ ก็ตาม 1x ก็ยังคงเท่ากับ 1 เสมอ ดังนั้นจึงไม่น่าสนใจ เนื่องจาก เราทราบว่ามันเป็นอะไรแน่ ๆ อยู่แล้ว
- เรายังไม่ทราบนะว่า เลขยกกำลังที่มีฐานเป็นจำนวนจริงบวกยกเว้น 1 และเลขชี้กำลังเป็นจำนวนจริงใด ๆ แสดงว่าเราจะต้องสนใจศึกษาเลขยกกำลังลักษณะนี้เป็นพิเศษ ซึ่งจะกล่าวถึงใน เรื่องฟังก์ชันเอกซ์โพเนนเชียลดังนี้
ข้อกำหนด (ฟังก์ชันเอกซ์โพเนนเชียล)
ฟังก์ชันเอกซ์โพเนนเชียล คือ f = { (x, y) Î R ´ R+ / y = ax , a > 0, a ¹ 1 }
ข้อตกลง ในหนังสือคณิตศาสตร์บางเล่มให้ข้อกำหนดของฟังก์ชันเอกซ์โพเนนเชียล เป็นฟังก์ชันที่อยู่ในรูป f(x) = kax เมื่อ k เป็นค่าคงตัวที่ไม่ใช่ 0 และ a เป็นจำนวนจริงบวกที่ไม่เป็น 1 แต่ในหลักสูตรมัธยมศึกษาตอนปลายนี้ จะถือว่าฟังก์ชันเอกซ์โพเนนเชียลจะอยู่ในรูป f(x) = ax เมื่อ a เป็น จำนวนจริงบวกที่ไม่เป็น 1 เท่านั้น
ข้อสังเกต จากข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล
- f(x) = 1x เป็นฟังก์ชันคงตัวเนื่องจาก 1x = 1 ดังนั้นในข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล จึงไม่สนใจ ฐาน (a) ที่เป็น 1
- f(x) = 1x ไม่เป็นฟังก์ชันเอ็กซ์โพเนนเชียล เนื่องจาก f(x) = 1x เป็นฟังก์ชันคงตัว
- จากเงื่อนไขที่ว่า y = ax, a > 0, a ¹ 1 ทำให้เราทราบได้เลยว่าฐาน (a) มีอยู่ 2 ลักษณะ คือ 0 < a < 1 กับ a > 1
- ฟังก์ชันเอกซ์โพเนนเชียลจะมีอยู่ 2 ชนิด โดยขึ้นอยู่กับลักษณะของฐาน (a) ดังนี้
ชนิดที่ 1 y = ax, 0 < a < 1
ชนิดที่ 2 y = ax, a > 1
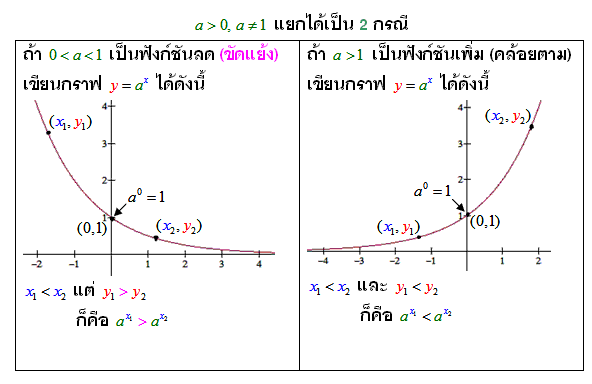
กราฟของฟังก์ชัน y = ax, 0 < a < 1
อสมการเอกซ์โพเนนเชียล
เทคนิคชุดที่ 1
การแก้อสมการเอกซ์โพเนนเชียลที่ทำฐานให้เหมือนกันได้
หลักการ
- ถ้า 0 < a < 1 (ฟังก์ชันลด) แล้ว
- ax1 > ax2 ก็ต่อเมื่อ x1 < x2
- ax1 < ax2 ก็ต่อเมื่อ x1 > x2
ข้อสังเกต
- ถ้า a > 1(ฟังก์ชันเพิ่ม) แล้ว
- ax1 > ax2 ก็ต่อเมื่อ x1 > x2
- ax1 < ax2 ก็ต่อเมื่อ x1 < x2
ข้อสังเกต ปลดฐาน หรือเติมฐาน คงเดิมเครื่องหมายอสมการ
สิ่งที่ควรเน้น คำตอบที่ได้จากการแก้อสมการ ไม่ต้องนำมาตรวจสอบคำตอบ
ยกเว้น ในกรณีที่มีการยกกำลังจำนวนคู่ จะต้องตรวจสอบคำตอบด้วย
เรื่องการแก้อสมการเอกซ์โพเนนเชียลนั้น มีสิ่งที่ต้องคำนึงอยู่แค่หนึ่งสิ่งที่สำคัญคือ กรณีฐานของเลขยกกำลังนั้นมีค่ามากกว่าศูนย์แต่น้อยกว่าหนึ่ง นอกนั้นไม่มีอะไรเลยครับ การแก้อสมการในกรณีที่เลขฐานมากกว่าศูนย์แต่น้อยกว่าหนึ่ง ต้องมีการสลับเครื่องหมายเป็นเครื่องหมายตรงกันข้าม ดังทฤษฏีต่อไปนี้
กรณีที่ฐาน 0<a<10<a<1
ถ้า ax>ayax>ay แล้ว x<yx<y ต้องสลับเครื่องหมายเป็นเครื่องหมายตรงกันข้าม
แต่ถ้า
กรณีที่ฐาน a>1a>1
ถ้า ax>ayax>ay แล้ว x>yx>y ฐานมากว่าหนึ่งไม่ต้องสลับเครื่องหมายนะครับ
เป็นดูตัวอย่างการแก้อสมการเอ็กซ์โพเนนเชียลกันเลย
ตัวอย่างที่ 1 จงแก้อสมการเอ็กซ์โพเนนเชียลต่อไปนี้
1) 4x+1>2x−34x+1>2x−3
วิธีทำ ขั้นตอนแรกต้องทำฐานให้เท่ากันก่อนครับ
4x+1>2x−34x+1>2x−3
22(x+1)>2x−322(x+1)>2x−3
22x+2>2x−322x+2>2x−3 จะเห็นว่าฐานเท่ากันแล้ว
ดังนั้นจะได้ เอาเลขชี้กำลังมาแก้อสมการต่อนะครับ ไม่ต้องสลับเครื่องหมายเพราะฐานคือ 2 มากกว่า 1
2x+2>x−32x+2>x−3
2x>x−3−22x>x−3−2
2x>x−52x>x−5
2x−x>−52x−x>−5
x>−5
การแก้อสมการเอกซ์โพเนนเชียล
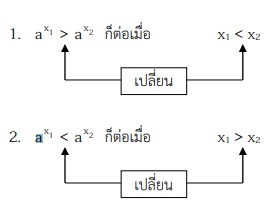
1. ถ้า 0 < a < 1 (ฟังก์ชันลด) แล้ว
สังเกตได้ว่า : สําหรับ 0 < a < 1 เมื่อปลดฐานหรือเติมฐาน เปลี่ยนเครื่องหมายอสมการ
- ถ้า a > 1(ฟังก์ชันเพิ่ม) แล้ว
- ax1 > ax2 ก็ต่อเมื่อ x1 < x2
- ax1 < ax2 ก็ต่อเมื่อ x1 > x2
2. ถ้า a > 1 (ฟังก์ชันเพิ่ม) แล้ว
- ถ้า a > 1(ฟังก์ชันเพิ่ม) แล้ว
- ax1 > ax2 ก็ต่อเมื่อ x1 > x2
- ax1 < ax2 ก็ต่อเมื่อ x1 < x2
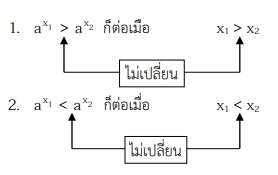
จุดสังเกต : สําหรับ a > 1 เมื่อปลดฐาน หรือเติมฐาน คงเดิมเครื่องหมายอสมการ
ฟังก์ชันลอการิทึม คืออะไร
- ฟังก์ชันอินเวอร์สของฟังก์ชันเอกซ์โพเนนเชียลสามารถเขียนใหม่ได้เป็น { (x, y) ∈ R+ ×R / y = logax, a > 0, a ≠ 1 }
- ฟังก์ชันอินเวอร์สของฟังก์ชันเอกซ์โพเนนเชียล ถูกเรียกใหม่ว่า ฟังก์ชันลอการิทึม
- logax อ่านว่า “ลอการิทึมเอกซ์ฐานเอ” หรือ “ล็อกเอกซ์ฐานเอ”






