ฟังก์ชัน ตรีโกณมิติ
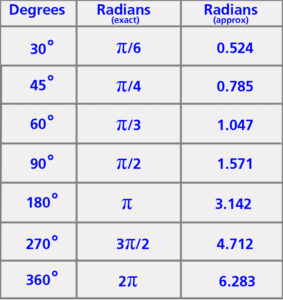
เปลี่ยนมุมในหน่วยเรเดียนเป็นองศา
หน่วยวัดมุม
โดยทั่วไปเราคุ้นเคยกับหน่วยวัดมุมอย่าง “องศา” กันมาอยู่แล้ว หากเป็นรูปสามเหลี่ยมด้านเท่า ก็จะมีมุมภายในมุมละ 60 องศา มุมฉากเท่ากับ 90 องศา เส้นตรงมีมุม 180 องศา และวงกลมที่เราทราบกันดีว่ามีมุมภายในเท่ากับ 360 องศา แม้ว่าองศาจะไม่ใช่หน่วยในระบบหน่วยวัดสากล (SI) แต่ก็ได้รับการยอมรับให้ใช้กันอย่างกว้างขวาง
เรเดียนคืออะไร
แม้ว่าเราจะใช้คำว่า “เรเดียน” ตามหลังตัวเลขบอกขนาดของมุม แต่แท้จริงแล้ว เรเดียนไม่ใช่หน่วย มันเป็นรูปแบบหนึ่งของการบอกขนาดมุมเท่านั้น เพียงแต่การเติมเรเดียนด้านหลังก็เพื่อให้เข้าใจตรงกันและใช้งานได้สะดวกขึ้น เรเดียนถูกใช้มานานแล้ว แต่กลับประกาศใช้และมีการให้คำจำกัดความประมาณปี 1870 โดยนักคณิตศาสตร์ โทมัส มูเยอร์ (Thomas Muir) และเจมส์ ทอมป์สัน (James Thompson) ซึ่งในเวลานั้นมีความลังเลระหว่างการใช้ rad, radial และ radian แต่ก็ปรับเปลี่ยนเป็นเรเดียนเมื่อปี 1874 และได้รับการตีพิมพ์เมื่อปี 1890 ในท้ายที่สุด
เรเดียนก็คือ อัตราส่วนระหว่าง ส่วนโค้งของวงกลมกับรัศมี หรือก็คือ θ = ส่วนโค้งของวงกลม/รัศมี หน่วยจึงหายไป ดังนั้น เรเดียนจึงไม่มีหน่วย หากสมมุติให้รัศมีวงกลมมีค่า 1 หน่วย ส่วนโค้งของวงกลมที่มีระยะจากรัศมีเส้นที่ 1 มายังรัศมีเส้นที่ 2 มีความยาว 1 หน่วยเท่ากับขนาดของรัศมี θ ก็จะมีค่าเท่ากับ 1 และเมื่อลองแบ่งวงกลมไปเรื่อย ๆ ทีละ θ = 1 จะได้มุมภายในวงกลมทั้งหมดเป็น θ = 6
สูตรเส้นรอบวง = 2πr และนิยาม θ = ส่วนโค้งของวงกลม/รัศมี
ซึ่งจะได้เป็น θ = 2πr/r
ดังนั้น θ = 2π
แต่ π = 3.14 หรือ 22/7 จึงได้เป็น θ = 2π = 2×3.14
ด้วยเหตุนี้ θ หรือมุมภายในวงกลมทั้งหมดจึงเท่ากับ 6.28 ซึ่งทำให้เราทราบว่า ส่วนโค้งของวงกลมที่เหลืออีกเล็กน้อยนั่นก็คือ 0.28