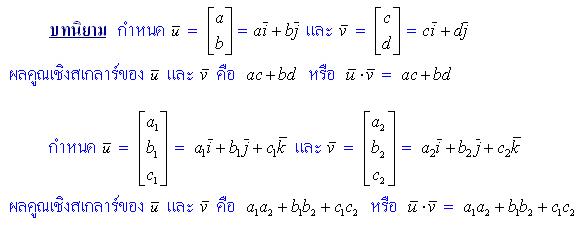เวกเตอร์ (vector)

ทำไมต้องเรียนเรื่องเวกเตอร์แน่นอนว่าถ้าเรายังเป็นมนุษย์โบราณและยังอาศัยอยู่ในถ้า เราคงไม่มีความจำเป็นต้องเรียนเรื่องเวกเตอร์อย่างแน่นอน เพราะว่าเรื่องนี ้คงไม่จ าเป็ นส าหรับมนุษย์ถ ้า แต่เนื่องจากเรา
เกิดมาในยุคนี ้ การไม่เรียนรู้อะไรเลย คงไม่ได้ เพราะว่าวิทยาการในปัจจุบันก้าวหน้าไปอย่างมากและการเรียนรู้ เกี่ยวกับเวกเตอร์ก็มีความจ าเป็ น เพราะว่าปริมาณหลายปริมาณที่เกี่ยวข้องกับ ชีวิตประจำวันของเราเป็นปริมาณเวกเตอร์ เช่น แรง ความเร็ว ฯลฯ

เวกเตอร์ คณิตศาสตร์ ม.ปลาย ประกอบด้วย

1. ระบบพิกัดฉากในสามมิติ

2. เวกเตอร์

3. ลักษณะของเวกเตอร์

4. การบวกเวกเตอร์

5. การลบเวกเตอร์

6. การคูณเวกเตอร์ด้วยสเกลาร์

7. เวกเตอร์หนึ่งหน่วย

8. เวกเตอร์ในระบบพิกัดฉาก 2 มิติ

9. เวกเตอร์ในระบบพิกัดฉาก 3 มิติ

10. สมบัติของเวกเตอร์

11. ขนาดของเวกเตอร์

12. เวกเตอร์หนึ่งหน่วยซึ่งมีทิศเดียวกับเวกเตอร์ที่กำหนด

13. โคไซน์แสดงทิศทาง

14. ผลคูณเชิงสเกลาร์

15. ผลคูณเชิงเวกเตอร์ เวกเตอร์ในสามมิติ การบอกปริมาณ ปริมาณมี 2 รูปแบบ คือ1. ปริมาณสเกลาร์ (scalar quantity) คือ ปริมาณที่บอกเฉพาะขนาด ไม่บอกทิศทาง เช่น ระยะทาง พื้นที่ อุณหภูมิ

เวกเตอร์ในเชิงเรขาคณิตได้ด้วยส่วนของเส้นตรงและลูกศร โดยที่ทิศทางของลูกศรแทนทิศทางของเวกเตอร์ และความยาวของลูกศรแทน ขนาดของเวกเตอร์ หางลูกศรเรียกว่า จุดเริ่มต้นของเวกเตอร์ หัวลูกศร เรียกว่า จุดสิ้นสุดของเวกเตอร์

สัญลักษณ์ที่ใช้

(รูปที่ 1)

บทนิยาม  1  ถ้าเวกเตอร์  u และ v เป็นเวกเตอร์ที่ไม่ใช่เวกเตอร์ศูนย์ แล้ว ผลบวกของเวกเตอร์  u และ v เขียนแทนด้วยเวกเตอร์  u + v  หาได้จากให้ตำแหน่งเวกเตอร์ v มีจุดเริ่มต้นอยู่ที่จุดสิ้นสุดของเวกเตอร์ u
เวกเตอร์ u + v  จะแทนด้วยลูกศรจากจุดเริ่มต้นของเวกเตอร์ u  ไปยังจุดสิ้นสุดของเวกเตอร์  v ดังรูปที่  2

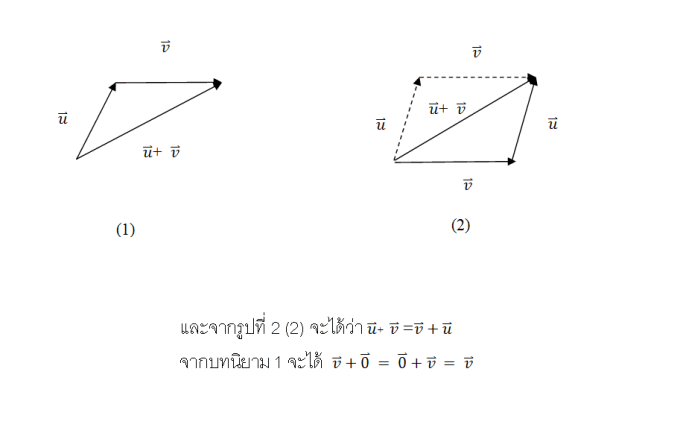(รูปที่ 2)

บทนิยาม 2 ให้เวกเตอร์ v เป็นเวกเตอร์ที่ไม่ใช่เวกเตอร์ศูนย์ และ k เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ แล้ว เวกเตอร์  kv หมายถึงเวกเตอร์ที่มีขนาดเท่ากับ |k| เท่าของเวกเตอร์ v เมื่อ k>0 เวกเตอร์ kv จะมีทิศทางเดียวกับ v และเมื่อ k<0 เวกเตอร์ kv มีทิศตรงข้ามกับเวกเตอร์ v และให้เวกเตอร์  kv =0 เมื่อ k =0

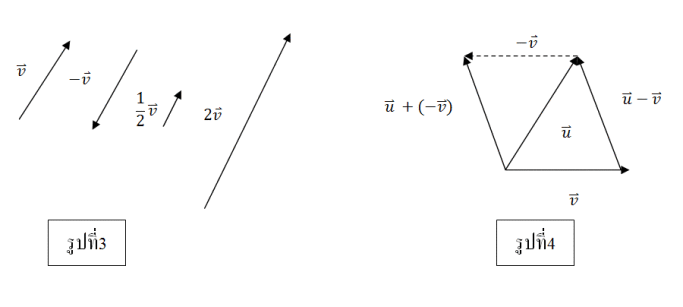จากรูปที่  3 ได้ว่าเวกเตอร์  v กับเวกเตอร์  Kv เป็นเวกเตอร์ที่ขนานกัน

สมบัติการบวกในระนาบ

1. u + v เป็นเวกเตอร์ในระนาบ สมบัติปิด
2. u + v = v + u สมบัติการสลับที่
3. u + (v + w) = (u + (v) + w สมบัติการเปลี่ยนกลุ่มได้
4. มี 0 โดยที่ 0 + u = u + 0 = u สมบัติการมีเอกลักษณ์
5. สำหรับทุก ๆ u จะมี -u โดยที่ -u + u = 0 = u + (-u) สมบัติการผกผัน
6. ถ้า u = v แล้ว w + v = w + u สมบัติการบวกด้วยเวกเตอร์ที่เท่ากัน

กราฟแสดงผลบวก u + v

ให้
u = ai + bj
v = ci + dj
u + v = (a + c)i + (b + d)j
u – v = (a – c)i + (b – d)j

เวกเตอร์ศูนย์

1. เวกเตอร์ศูนย์ 0 (0) คือเวกเตอร์ที่มีขนาดศูนย์หน่วย
2. จุดเริ่มต้นและจุดสิ้นสุดของเวกเตอร์ศูนย์เป็นจุดเดียวกัน

การคูณเวกเตอร์ด้วยสเกลาร์

ให้เวกเตอร์ u จะเขียน 2u ได้ 2u = u + u

สมบัติการคูณเวกเตอร์ด้วยสเกลาร์

ให้ u และ v เป็นเวกเตอร์ใด ๆ ในระนาบ a และ b เป็นจำนวนจริง
1. au เป็นเวกเตอร์ในระบบ สมบัติปิด
2. a(bu) = (ab)u สมบัติการเปลี่ยนกลุ่ม
3. (a + b)u = au + bu สมบัติการแจกแจง
4. a(u + v) = au + av สมบัติการแจกแจง
5. 1u = u
6. ถ้า au = 0 แล้ว a = 0 หรือ u = 0

เวกเตอร์หนึ่งหน่วย (Unit vector)

เวกเตอร์หนึ่งหน่วย คือ เวกเตอร์ที่มีขนาดเท่ากับ 1

มองภาพเห็นไหม ยกตัวอย่างให้เห็นภาพชัดเจน

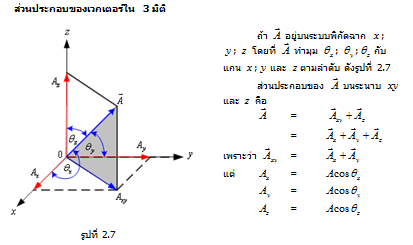
ส่วนประกอบของเวกเตอร์

เวกเตอร์หนึ่งหน่วย คือเวกเตอร์ที่มีขนาด 1 หน่วย และมีทิศทางตามเวกเตอร์ที่พิจารณา เช่น ให้ เป็นเวกเตอร์ที่มีขนาดเท่ากับ และ เป็นเวกเตอร์หนึ่งหน่วย ที่มีทิศเดียวกับเวกเตอร์ ดังรูป

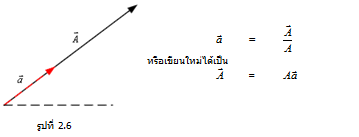
ดังนั้นในระบบพิกัดแกนมุมฉาก เวกเตอร์หนึ่งหน่วยแทนด้วย

มีขนาด 1 หน่วยทิศตามแกน X

มีขนาด 1 หน่วยทิศตามแกน Y

มีขนาด 1 หน่วยทิศตามแกน Z

โดยเวกเตอร์ทั้งสามตั้งฉากซึ่งกันและกัน และเวกเตอร์ทั้งสามจะเรียงกันในทิศทวนเข็มนาฬิกา

จากตัวอย่างที่ 2.3  คำตอบที่ได้สามารถเขียนใหม่ได้เป็น เป็นการเขียนในรูปแบบมาตรฐานซึ่งมีความสะดวกมากเมื่อนำไปใช้ในการบวกและการคูณเวกเตอร์

รูปแแบบทั่ว ๆ ไปของเวกเตอร์เขียนได้ดังนี้ เมื่อ คือส่วนประกอบบนแกน ของ  ; คือส่วนประกอบบนแกน ของ ; คือส่วนประกอบบนแกน ของ เป็นเวกเตอร์ใน 3 มิติ

เวกเตอร์หนึ่งหน่วย (Unit vector)

เวกเตอร์หนึ่งหน่วย (Unit vector)

ผลคูณเชิงสเกลาร์

ผลคูณเชิงสเกลาร์ของเวกเตอร์ หรือภาษาอังกฤษคือ dot product  คือการนำเวกเตอร์มาดอทกันผลลัพธ์จากการนำเวกเตอร์มาดอทกันนี้จะเป็นสเกลาร์หรือว่าตัวเลข  เรามาดูนิยามของมันเลยครับ