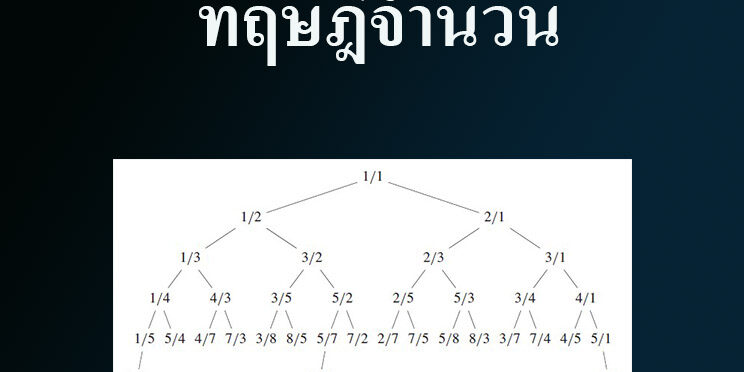
ทฤษฎีจำนวนพื้นฐาน
ตามหลักการทางคณิตศาสตร์ จำนวนธรรมชาติ (natural number) อาจนิยามได้ในรูปแบบตามหลักการของทฤษฎีจำนวน ก็คือ จำนวนเต็มบวก หรือ จำนวนนับ (1, 2, 3, 4, …) แต่หาในกรณีนิยามในรูปแบบของหลักการในเชิงเซต ตรรกศาสตร์ และวิทยาการคำนวณ อาจกล่าวได้ว่า 0 เป็นจำนวนธรรมชาติตัวแรก หรือนิยามได้ว่า จำนวนธรรมชาติ คือ จำนวนเต็มไม่เป็นลบ (0, 1, 2, 3, 4, …)
หรือสรุปได้ว่า จำนวนธรรมชาติ เป็นจำนวนที่เกิดขึ้นในทางธรรมชาติโดยธรรมดา ชัดเจน ไม่ซับซ้อน เช่น จำนวนไม่เป็นลบทั้งหมด อาจเขียนเซต ของ จำนวนธรรมชาติ โดยใช้สัญลักษณ์ N ซึ่งสามารถกำหนดได้สองรูปแบบ คือ N = {0, 1, 2, 3, …} และ N = (1, 2, 3, 4, …}
มีสันนิษฐานว่าจำนวนธรรมชาติเกิดขึ้นอย่างเป็นธรรมชาติตามรูปแบบของการนับหรือจำนวนนับ ซึ่งก็หมายถึงลำดับการนับของตัวเลขเพื่อแสดงค่าจำนวน ดังนั้น ถ้าถามว่าจำนวนธรรมชาติมีความสำคัญอย่างไร ? ก็คงตอบได้ว่า ไม่อาจกล่าวได้ว่ามีความสำคัญ แต่เป็นหลักการพื้นทางของวิชาคณิตศาสตร์ ที่ควรทำความเข้าใจเสียมากกว่า ซึ่งโดยปกติ เราใช้จำนวนธรรมชาติในการนับและการจัดอันดับเป็นส่วนใหญ่ ตัวอย่างการนับ เช่น บ้านหลังนี้มีจำนวนสมาชิกอยู่ทั้งหมด 5 คน ส่วนตัวอย่างการจัดอันดับเช่น กรุงเทพมหานครเป็นเมืองที่มีประชากรหนาแน่นเป็นอันดับที่ 1 ในประเทศ เป็นต้น
เป็นสาขาหนึ่งของทฤษฎีจำนวนที่ศึกษาจำนวนโดยไม่ได้ใช้ความรู้ชั้นสูงจากสาขาอื่นเลย ปัญหาที่สาขานี้สนใจส่วนใหญ่แล้วจะเกี่ยวกับสมบัติที่น่าสนใจต่าง ๆ ของจำนวนเต็ม เช่น การหารลงตัว (divisibility) การแยกตัวประกอบเฉพาะ (prime factorization) และ จำนวนสมบูรณ์ (perfect number) เป็นต้น ทฤษฎีบทในทฤษฎีจำนวนพื้นฐานจำนวนมากมีประยุกต์ใช้ในคณิตศาสตร์สาขาอื่น เช่น ทฤษฎีบทเศษเหลือของจีน (Chinese remainder theorem) ในขณะที่ทฤษฎีบทเล็กของแฟร์มาต์ (Fermat’s little theorem) และ ทฤษฎีบทของออยเลอร์ (Euler’s theorem) ถูกนำไปใช้ในงานวิจัยด้านทฤษฎีพื้นฐานของการเข้ารหัส
ปัญหาบางอย่างในสาขานี้สามารถอธิบายให้เข้าใจได้ง่าย แต่ยังเป็นปัญหาเปิดจนถึงปัจจุบัน เช่น
- ข้อความคาดการณ์ของโกลด์บาช (Goldbach conjecture)
- ข้อความคาดการณ์ของคาตาลอง (Catalan’s conjecture)
- ข้อความคาดการณ์จำนวนเฉพาะคู่แฝด (Twin prime conjecture)
ทฤษฎีบทที่มีชื่อเสียงของสาขาทฤษฎีจำนวนเชิงวิเคราะห์คือ ทฤษฎีบทจำนวนเฉพาะ ในขณะที่หลายปัญหาเปิดในสาขานี้ก็เป็นที่รู้จักกันทั่วไป เช่น ข้อความคาดการณ์ฮาร์ดี-ลิตเติลวูด ปัญหาวอร์ริง และ สมมติฐานรีมันน์
เครื่องมือที่สำคัญในสาขาทฤษฎีจำนวนเชิงวิเคราะห์เช่น วิธีวงกลม วิธีตะแกรง และ แอล-ฟังก์ชัน นอกจากนี้ทฤษฎีของแบบมอดูลาร์ยังเป็นแกนหลักสำคัญของทฤษฎีจำนวนวิเคราะห์สมัยใหม่ด้วย
ทฤษฎีจำนวนเบื้องต้น
นิยาม : ให้ m และ n เป็นจำนวนเต็ม
โดยที่ n หาร m ลงตัว ก็ต่อเมื่อ มีจำนวน q ที่ทำให้ m = nq
เรียก n ว่าเป็น ตัวหาร ของ m และ
เรียก m ว่าเป็นพหุคูณ ของ n
จากนิยามดังกล่าว มีการใช้สัญลักษณ์ ดังนี้
n|m แทน n หาร m ลงตัว หรือ m หารด้วย n ลงตัว
n|/m แทน n หาร m ไม่ลงตัว หรือ m หารด้วย n ไม่ลงตัว
การหารลงตัว
a|b หมายถึง “b หารด้วย a ลงตัว” หรือ “a หาร b ลงตัว”
b/a= c โดยที่ c เป็นจำนวนเต็ม
สมบัติ
- ถ้า a|b และ b|c แล้ว a|c
- ถ้า a และ b เป็นจำนวนเต็มบวก และ a|b แล้ว a≤b
- ถ้า a, b, c เป็นจำนวนเต็ม โดย a|b และ a|c แล้ว a|(bx+cy) เมื่อ x, y เป็นจำนวนเต็มใด ๆ
การหารเหลือเศษ
a/b= c เศษ d ⟶ a=b.c+d
โดยที่ a, b, c, d เป็นจำนวนเต็ม และ 0 ≤ d < |b|
คำแนะนำเพิ่มเติม :
- ถ้า a/b เหลือเศษเท่ากับ d แล้ว (m.a)/b เหลือเศษเท่ากับเศษเหลือของ (m.d)/b
- ถ้า a/b เหลือเศษเท่ากับ d แล้ว am/b เหลือเศษเท่ากับเศษเหลือของ dm/b