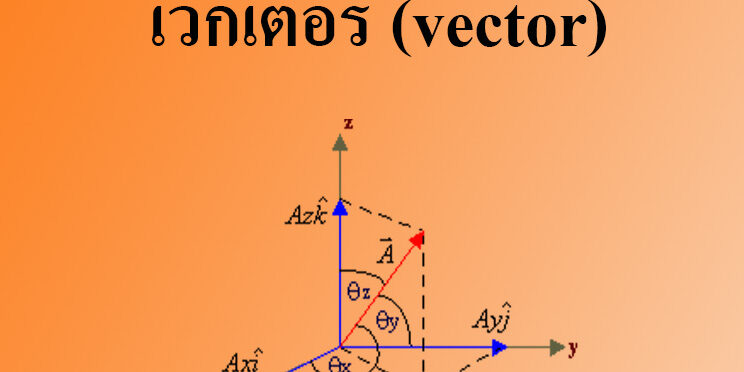
เวกเตอร์ (vector)
เวกเตอร์ (อังกฤษ: vector) เป็นปริมาณในทางคณิตศาสตร์ และ ฟิสิกส์ ปริมาณเวกเตอร์ประกอบไปด้วยขนาด (magnitude) และทิศทาง (direction) ซึ่งสามารถใช้ดำเนินการทางคณิตศาสตร์บนปริภูมิเวกเตอร์ (vector space) ต่างจากปริมาณสเกลาร์ที่อธิบายปริมาณด้วยขนาดเพียงอย่างเดียว
เวกเตอร์มีการใช้กันในหลายสาขานอกเหนือจากทางคณิตศาสตร์ โดยเฉพาะในทางวิทยาศาสตร์ฟิสิกส์ และเคมี เช่น การกระจัด
- เวกเตอร์และสมบัติของเวกเตอร์
- เวกเตอร์ในระบบพิกัดฉาก
- ผลคูณเชิงสเกลาร์
- ผลคูณเชิงเวกเตอร์
- การหาพื้นที่และปริมาตร
เวกเตอร์ ปริมาณมี 2 แบบ คือสเกลาร์ กับเวกเตอร์
สเกลาร์ เป็น ปริมาณที่มีแต่ขนาด เช่น พื้นที่ อุณหภูมิ ความยาว เป็นต้น
เวกเตอร์ เป็น ปริมาณที่มีทั้งขนาดและทิศทาง เช่นความเร็ว แรง เป็นต้น
เราสามารถแทนเวกเตอร์ในเชิงเรขาคณิตได้ด้วยส่วนของเส้นตรงและลูกศร โดยที่ทิศทางของลูกศรแทนทิศทางของเวกเตอร์ และความยาวของลูกศรแทน ขนาดของเวกเตอร์ หางลูกศรเรียกว่า จุดเริ่มต้นของเวกเตอร์ หัวลูกศร เรียกว่า จุดสิ้นสุดของเวกเตอร์
สัญลักษณ์ที่ใช้
(รูปที่ 1)
บทนิยาม 1 ถ้าเวกเตอร์ u และ v เป็นเวกเตอร์ที่ไม่ใช่เวกเตอร์ศูนย์ แล้ว ผลบวกของเวกเตอร์ u และ v เขียนแทนด้วยเวกเตอร์ u + v หาได้จากให้ตำแหน่งเวกเตอร์ v มีจุดเริ่มต้นอยู่ที่จุดสิ้นสุดของเวกเตอร์ u
เวกเตอร์ u + v จะแทนด้วยลูกศรจากจุดเริ่มต้นของเวกเตอร์ u ไปยังจุดสิ้นสุดของเวกเตอร์ v ดังรูปที่ 2
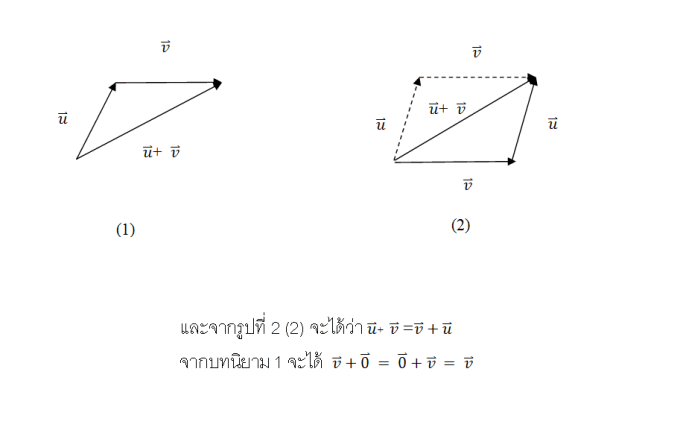 (รูปที่ 2)
(รูปที่ 2)
บทนิยาม 2 ให้เวกเตอร์ v เป็นเวกเตอร์ที่ไม่ใช่เวกเตอร์ศูนย์ และ k เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ แล้ว เวกเตอร์ kv หมายถึงเวกเตอร์ที่มีขนาดเท่ากับ |k| เท่าของเวกเตอร์ v เมื่อ k>0 เวกเตอร์ kv จะมีทิศทางเดียวกับ v และเมื่อ k<0 เวกเตอร์ kv มีทิศตรงข้ามกับเวกเตอร์ v และให้เวกเตอร์ kv =0 เมื่อ k =0
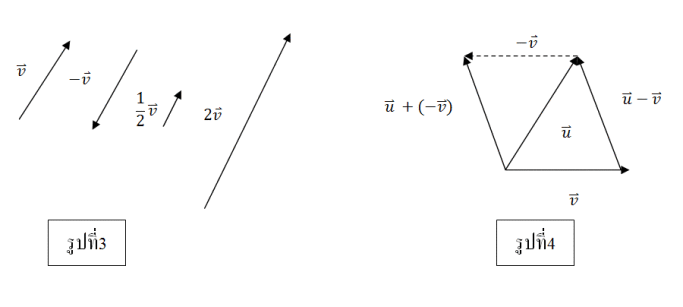 จากรูปที่ 3 ได้ว่าเวกเตอร์ v กับเวกเตอร์ Kv เป็นเวกเตอร์ที่ขนานกัน
จากรูปที่ 3 ได้ว่าเวกเตอร์ v กับเวกเตอร์ Kv เป็นเวกเตอร์ที่ขนานกัน
 เวกเตอร์ในระบบพิกัดฉากในปริภูมิสามมิติ
เวกเตอร์ในระบบพิกัดฉากในปริภูมิสามมิติ
ให้เวกเตอร์ v เป็นเวกเตอร์ในปริภูมิ 3 มิติในระบบพิกัดฉาก ซึ่งมีจุดเริ่มต้นอยู่ที่จุดกำเนิด และจุดสิ้นสุดอยู่ที่จุด (x1,y1,z1) ดังรูปที่ 5 เรียกพิกัด x1,y1และ z1ว่า ส่วนประกอบเวกเตอร์ และเขียนแทนด้วย
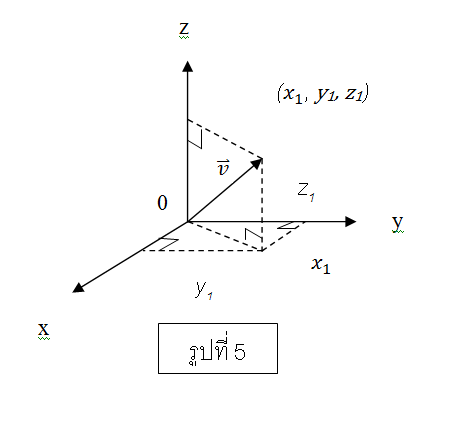

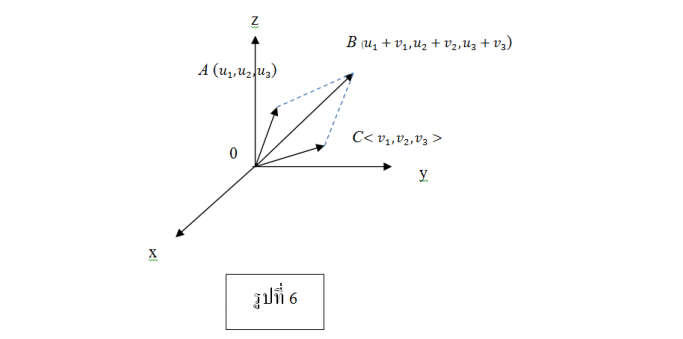
เวกเตอร์ในระบบพิกัดฉาก 2 มิติและ 3 มิติ
เนื้อหาประกอบด้วย
2.1 ระบบพิกัด
2.2 เวกเตอร์
2.3 ส่วนประกอบของเวกเตอร์
2.4 การบวกเวกเตอร์
2.5 เวกเตอร์ตำแหน่ง
2.6 การคูณเวกเตอร์

เวกเตอร์เป็นเครื่องมือทางคณิตศาสตร์อย่างหนึ่ง ซึ่งดูเหมือนไม่มีความจำเป็นแตเป็นเครื่องมืออย่างแรกที่ต้องใช้ อย่างไรก็ตามในการศึกษาทางฟิสิกส์เวกเตอร์เป็นเครื่องมือที่มีความสำคัญ เพื่อช่วยในอำนวยความสะดวกในการคำนวณ
2.1 ระบบพิกัด (แกนอ้างอิง)
ระบบพิกัดมีความสำคัญเพื่อช่วยในการวัดมีความหมาย เช่นอีก 800 m ถึงอาคารวิทยาศาสตร์เป็นการบอกที่ไม่สมบูรณ์ เนื่องจากไม่ทราบว่าเริ่มต้นที่ตำแหน่งใด
ดังนั้นในการกำหนดระบบพิกัดต้องทราบ
ก. จุดเริ่มต้น
ข. ชนิดของระบบพิกัด (พิกัดฉาก ; พิกัดเชิงขั้ว ; พิกัดทรงกระบอก)
ค. ทิศตามแกน
ระบบพิกัดแบบมาตรฐานใน 2 มิติ
ได้แก่ระบบพิกัดฉาก (Cartesian) และ ระบบพิกัดเชิงขั้ว (Polar)
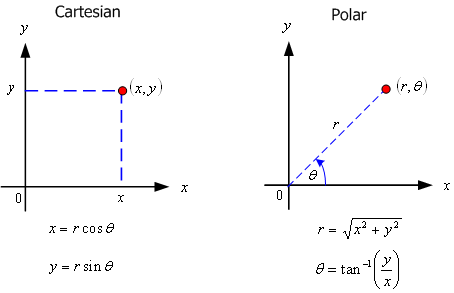
ระบบพิกัดแบบมาตรฐานใน 3 มิติ
ได้แก่ระบบพิกัดฉาก (Cartesian) และ ระบบพิกัดทรงกระบอก (Cylindrical) และระบบพิกัดทรงกลม (Spherical)
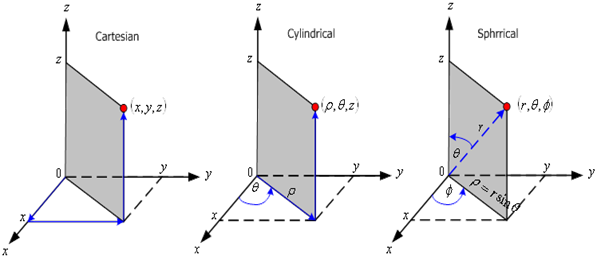
รูปที่ 2.3 ระบบพิกัดฉากใน 3 มิติ
2.2 เวกเตอร์
สเกลาร์ : ปริมาณที่มีเฉพาะขนาดอย่างเดียว
เวกเตอร์ : ปริมาณที่มีทั้งขนาดและทิศทาง
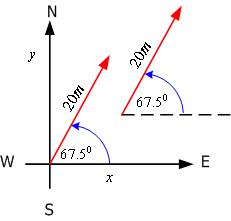
รูปที่ 2.1 แสดงระบบพิกัดใน 2 มิติ
ลคูณเชิงสเกลาร์ (Scalar Product or Product)
ผลคูณเชิงสเกลาร์ หมายถึง ผลคูณของเวกเตอร์ที่ได้ผลลัพธ์เป็นสเกลาร์ ซึ่งนิยามในสองมิติ และสามมิติ ได้ดังนี้
บทนิยาม ถ้า ![]() = x1
= x1 ![]() + y1
+ y1 ![]() และ
และ ![]() = x2
= x2 ![]() + y2
+ y2 ![]()
ผลคูณเชิงสเกบาร์ของ ![]() และ
และ ![]() คือ x1x2+ y1 y2
คือ x1x2+ y1 y2
ถ้า ![]() =x1
=x1![]() + y1
+ y1 ![]() +z1
+z1![]() และ
และ ![]() =x2
=x2![]() +y2
+y2 ![]() +z2
+z2 ![]()
ผลคูณเชิงสเกลาร์ของ ![]() และ
และ ![]() คือ x1x2+ y1 y2+ z1z2
คือ x1x2+ y1 y2+ z1z2
ผลคูณเชิงสเกลาร์ของ ![]() และ
และ ![]() เขียนแทนด้วย
เขียนแทนด้วย ![]() ,
, ![]()
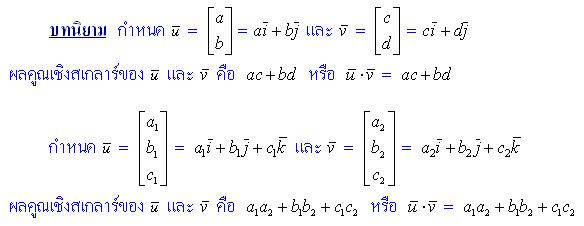
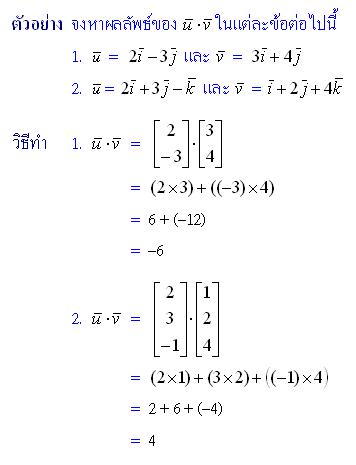
ผลคูณเชิงเวกเตอร์ (cross – vector Product )


เวกเตอร์เรื่องพื้นที่และปริมาตร