ตรรกศาสตร์เบื้องต้น ม.4 (Mathematical Logic )

ในเรื่องตรรกศาสตร์นี้ เราจะสนใจหาว่า ประโยคต่างๆ เป็นจริง หรือ เท็จแต่ก่อนอื่น ต้องรู้ว่า ไม่ใช่ทุกประโยค ที่จะเอามาหาความจริงได้
เช่น ถ้าอยากรู้ว่าประโยค “กินอะไรดี” เป็น จริง หรือ เท็จ คงตอบลำบาก“ประพจน์” คือ ประโยคที่เป็นจริง หรือ เท็จ ได้อย่างใดอย่างหนึ่งเพียงอย่างเดียว
เช่น ประเทศไทยอยู่ในทวีปเอเชีย → เป็นประพจน์ เพราะบอกได้ว่าเป็นจริง 3 > 5 → เป็นประพจน์เพราะบอกได้ว่าเป็นเท็จ
ขณะนี้ มีผู้หญิง 3,674,196 คน ใน กทม. → เป็นประพจน์ ถึงจะไม่รู้ว่าจริงหรือเท็จ แต่ถ้าช่วยกันนับดูก็จะรู้ว่า
จริงหรือเท็จซักอย่าง แน่นอน ประโยคที่ไม่ใช่ประพจน์ คือ ประโยคที่ท ายังไงก็บอกไม่ได้ว่าจริงหรือเท็จ
เช่น ประโยคค าถาม ค าสั่ง ค าขอร้อง ค าอุทาน สุภาษิต รวมถึงประโยคที่มีตัวแปร
เช่น กินอะไรดี → ไม่ใช่ประพจน์ เพราะเป็นประโยคคำถาม 𝑥 > 5 → ไม่ใช่ประพจน์ เพราะมีตัวแปร (ถ้า 𝑥 เป็น 8 จะจริง แต่ถ้า 𝑥 เป็น 1 จะเท็จ)
ในเรื่องตรรกศาสตร์นี้ เราจะสนใจศึกษาเฉพาะประโยคที่เป็นประพจน์เท่านั้น
โดยเรานิยมใช้ตัวอักษร 𝑝, 𝑞, 𝑟 เป็นสัญลักษณ์แทนประโยคที่เป็นประพจน์
เช่น ให้ 𝑝 แทนประพจน์ “เมื่อวานฝนตก”
ให้ 𝑞 แทนประพจน์ “ประเทศไทยมี 76 จังหวัด” เป็นต้น

ตรรกศาสตร์เบื้องต้น

1. ประพจน์

         ประพจน์ คือ ประโยคบอกเล่าหรือปฏิเสธที่มีค่าความจริงเป็นจริงหรือเท็จ

                                     อย่างใดอย่างหนึ่งเท่านั้น
                    ตัวอย่าง
                     ประโยคที่เป็นประพจน์ 
                                ดาวอังคารเป็นดาวเคราะห์                                  (จริง)
                                จังหวัดลพบุรีไม่อยู่ทางภาคใต้ของประเทศไทย    (จริง)
                                5 ≠ 8                                                               (จริง)
                                19 + 4 ≠ 23                                                     (เท็จ)
                                π เป็นจำนวนตรรกยะ                                         (เท็จ)
                    ประโยคที่ไม่เป็นประพจน์ 
ได้แก่ ข้อความที่อยู่ในรูปของ คำถาม คำสั่ง คำขอร้อง คำอุทาน คำอ้อนวอน คำแสดงความปรารถนา สุภาษิตคำพังเพย ประโยคเปิด เพราะข้อความดังกล่าวไม่สามารถบอกค่าความจริงได้
ตัวอย่างประโยคที่ไม่เป็นประพจน์ 
                                คำถาม  เช่น  3 หารด้วย 2 มีค่าเท่าไร
                                คำสั่ง  เช่น  จงยืนขึ้น
                                คำขอร้อง  เช่น  ช่วยกันรักษาความสะอาด
                                คำอ้อนวอน  เช่น  โปรดเมตตาด้วยเถิด
                                คำแสดงความปรารถนา  เช่น  อยากเห็นหน้าเธออีกสักครั้ง
                                คำอุทาน  เช่น  โอ้ย
                                สุภาษิตคำพังเพย  เช่น  วัวหายล้อมคอก
                                ประโยคเปิด  เช่น  เขาเป็นนักกีฬา

………………………………………………………………………………………………………

2. 
   การเชื่อมประพจน์
        ถ้าให้ p และ q เป็นประพจน์ เมื่อนำประพจน์มาเชื่อมกันด้วยตัวเชื่อมแล้ว เราเรัยกประพจน์ใหม่ว่า ประพจน์เชิงประกอบ ซึ่งตัวเชื่อมที่ใช้จะมี 5 ตัว คือ

                  1) ตัวเชื่อม และ  ใช้สัญลักษณ์ คือ ” ∧ “

                  2) ตัวเชื่อม หรือ  ใช้สัญลักษณ์ คือ  ” ∨ “

                  3) ตัวเชื่อม ถ้า… แล้ว…    ใช้สัญลักษณ์ คือ ” → “

                  4) ตัวเชื่อม ก็ต่อเมื่อ  ใช้สัญลักษณ์ คือ ” ↔ ”
5) ตัวเชื่อม นิเสธ  ใช้สัญลักษณ์แทนด้วย ” ~ “

แบบฝึกหัด
1. จงพิจารณาว่า ข้อใดต่อไปนี้เป็นประพจน์
1. ปิดหน้าต่างให้หน่อย 2. 4 + 7 = 12
3. หนังสือเรียนวิชาคณิตศาสตร์ 4. เชียงใหม่ ไม่ใช่เมืองหลวงของไทย
5. สุนัขปกติ มี 4 ขา 6. สุนัขปกติมี 3 ขา
7. เขาเป็นคนดี 8. หนึ่งวัน มี 30 ชั่วโมง

การเชื่อมประพจน์
เราสามารถน าประพจน์ต่างๆ มา “เชื่อม” กันได้ เช่น “เมื่อวานฝนตก และ ประเทศไทยมี 76 จังหวัด”
ค าเชื่อมที่จะได้เรียนในบทนี้ ได้แก่
1 …… และ ……

2 …… หรือ ……
3 ถ้า …… แล้ว ……

4 …… ก็ต่อเมื่อ ……

5 ไม่ ……

 สรุปการอ้างเหตุผลและตัวอย่าง

การอ้างเหตุผลคือ การอ้างว่า เมื่อมีประพจน์ p₁,p₂,…p_n, ชุดหนึ่ง แล้วสามารถสรุปประพจน์ C ประพจน์หนึ่งได้ การอ้างเหตุผลประกอบด้วยส่วนสำคัญสองส่วนคือ เหตุหรือสิ่งที่กำหนดให้ ได้แก่ ประพจน์ p₁,p₂,…p_n, และ ผลหรือข้อสรุป คือ ประพจน์ C โดยใช้ตัวเชื่อม ∧ เชื่อมเหตุทั้งหมด เข้าด้วยกัน และใช้ตัวเชื่อม → เชื่อมส่วนที่เป็นเหตุกับผลดังนี้

(p₁ ∧ p₂ ∧ … ∧ p_n,) → C

จะกล่าวว่า การอ้างเหตุผลนี้ สมเหตุสมผล (valid) ถ้ารูปแบบของประพจน์ (p₁ ∧ p₂ ∧ … ∧ p_n,) → C เป็นสัจนิรันดร์ และจะกล่าวว่า การอ้างเหตุผลนี้ ไม่สมเหตุสมผล (invalid) ถ้ารูปแบบของประพจน์ (p₁ ∧ p₂ ∧ … ∧ p_n,) → C ไม่เป็นสัจนิรันดร์ ดังนั้น ในการตรวจสอบความสมเหตุสมผลจึงใช้วิธีเดียว กับการตรวจสอบสัจนิรันดร์

ตัวอย่าง

กำหนดให้ p และ q เป็นประพจน์ จงพิจารณาว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่

เหตุ

1. p→q
2. p

ผล q

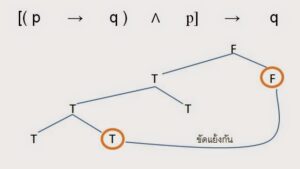
วิธีทำ ขั้นที่ 1 ใช้ ∧ เชื่อมเหตุเข้าด้วยกัน และใช้ → เชื่อมส่วนที่เป็นเหตุกับผล จะได้รูปแบบของประพจน์คือ [(p → q) ∧ p]→q

ขั้นที่ 2ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่ สมมติให้[(p → q) ∧ p]→q เป็นเท็จ

จากแผนภาพ แสดงว่า รูปแบบของประพจน์ [(p → q) ∧ p]→q เป็นสัจนิรันดร์

ดังนั้น การอ้างเหตุผลนี้สมเหตุสมผล

ตัวอย่าง

กำหนดให้ p และ q เป็นประพจน์ จงพิจารณาว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่

เหตุ

1. p→q
2. ∼p

ผล ∼q

วิธีทำ ขั้นที่ 1 ใช้ ∧ เชื่อมเหตุเข้าด้วยกัน และใช้ → เชื่อมส่วนที่เป็นเหตุกับผล จะได้รูปแบบของประพจน์คือ [(p → q) ∧ ∼p]→∼q

ขั้นที่ 2ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่ สมมติให้[(p → q) ∧ ∼p]→∼q เป็นเท็จ

จากแผนภาพ มีกรณีที่ p เป็นเท็จ และ q เป็นจริง ที่ทำให้ [(p → q) ∧ ∼p]→∼q เป็นเท็จ

แสดงว่า รูปแบบของประพจน์ [(p → q) ∧ ∼p]→∼q ไม่เป็นสัจนิรันดร์

ดังนั้น การอ้างเหตุผลนี้ไม่สมเหตุสมผล

ข้อสังเกต
1) การเชื่อมประพจน์ด้วยตัวเชื่อม และ  ” ∧ ”  จะเป็น T เมื่อ p และ q เป็น T ทั้งคู่
2) การเชื่อมประพจน์ด้วยตัวเชื่อม หรือ  ” ∨ ”  จะเป็น F เมื่อ p และ q เป็น F ทั้งคู่
3) การเชื่อมประพจน์ด้วยตัวเชื่อม ถ้า… แล้ว… ” → ”  จะเป็น F เมื่อ p เป็น T และ q เป็น F
4) การเชื่อมประพจน์ด้วยตัวเชื่อม ก็ต่อเมื่อ  ” ↔ ”  จะเป็น T เมื่อ p และ q มีค่าความจริงตรงกัน

3. การสร้างตารางค่าความจริง
กำหนด p , q , r เป็นประพจน์ที่ไม่ได้กำหนดค่าความจริงมาให้ จะเรียกประพจน์ที่มีตัวเชื่อมว่า รูปแบบประพจน์ เช่น ~p , p ∧ q , p → q , ( p ∨ q ) ↔ r เป้นต้น
ในการหาค่าความจริงของรูปแบบประพจน์ จะต้องพิจารณาค่าความจริงที่เป็นไปได้ของประพจน์ย่อยทุกกรณี โดยการสร้างตารางค่าความจริง
จำนวนกรณีที่พิจารณา = 2ⁿ กรณี
เมื่อ n คือ จำนวนประพจน์ย่อยของรูปแบบประพจน์นั้น

4. ประพจน์ที่สมมูลกัน
ประพจน์สองประพจน์ใด จะสมมูลกันก็ต่อเมื่อประพจน์ทั้งสองมีค่าความจริงเหมือนกันทุกกรณี ใช้สัญลักษณ์ ≡ แทนคำว่า สมมูล ประพจน์ที่สมมูลกันจะสามารถใช้แทนกันได้ เนื่องจากมีค่าความจริงเหมือนกันทุกกรณี
การตรวจสอบว่าประพจน์สมมูลกันหรือไม่ ทำได้ 2 วิธี ดังนี้

4.1 ใช้ตารางแสดงค่าความจริง
ตัวอย่าง จงตรวจสอบว่าประพจน์ต่อไปนี้สมมูลกันหรือไม่
1. p → q กับ  ~p ∨ q

จะเห็นว่า ค่าความจริงของ p → q กับ  ~p ∨ q ตรงกันกรณีต่อกรณี
ดังนั้น p → q สมมูลกับ  ~p ∨ q

2. ~p ∧ q กับ p → q

จะเห็นว่า ค่าความจริงของ ~p ∧ q กับ p → q มีบางกรณีต่างกัน
ดังนั้น ~p ∧ q ไม่สมมูลกับ p → q

4.2 ใช้รูปแบบของประพจน์ที่สมมูลกัน
รูปแบบของประพจน์ที่สมมูลกันที่สำคัญ
1. p ∧ ~p ≡ F
2. p ∨ ~p ≡ T
3. p ∧ T ≡ p
4. p ∨ F ≡ p
5. ~(~p) ≡ p
6. p ∨ q ≡ q ∨ p
7. p ∧ q ≡ q ∧ p
8. ( p ∨ q ) ∨ r ≡ p ∨ ( q ∨ r ) ≡ p ∨ q ∨ r
9. ( p ∧ q ) ∧ r ≡ p ∧ ( q ∧ r ) ≡ p ∧ q ∧ r
10. p ∨ ( q ∧ r ) ≡ ( p ∨ q ) ∧ ( p ∨ r )
11. p ∧ ( q ∨ r ) ≡ ( p ∧ q ) ∨ ( p ∧ r )
12. ~( p ∨ q ) ≡ ~p ∧ ~q
13. ~( p ∧ q ) ≡ ~p ∨ ~q
14. p → q ≡ ~q → ~p
15. p → q ≡ ~p ∨ q
16. ~( p → q ) ≡ p ∧ ~q
17. p ↔ q ≡ ( p → q ) ∧ ( q → p )

5. สัจนิรันดร์
ประพจน์ที่เป็นสัจนิรันดร์ คือ รูปแบบของประพจน์ที่มี ค่าความจริงเป็นจริงเสมอ ไม่ว่าประพจน์ย่อยจะมีค่าความจริงเป็น จริง หรือ เท็จ ก็ตาม เช่น p ∨ ~p , p → p , ~( p ∧ ~p ) , p ↔ p เป็นต้น
การตรวจสอบว่าประพจน์ใดเป็นสัจนิรันดร์ ทำได้ดังนี้
1. ใช้ตารางแสดงค่าความจริง
ตัวอย่าง จงตรวจสอบว่าประพจน์ต่อไปนี้ เป็นสัจนิรันดร์หรือไม่
1. [ ( p → q ) ∧ p ] → q

จะเห็นว่ารูปแบบของประพจน์  [ ( p → q ) ∧ p ] → q มีค่าจริงเป็นจริงทุกกรณี
ดังนั้น [ ( p → q ) ∧ p ] → q เป็น สัจนิรันดร์

2. ใช้วิธีการหาข้อขัดแย้ง
ตัวอย่าง จงตรวจสอบว่าประพจน์ต่อไปนี้ เป็นสัจนิรันดร์หรือไม่
1. ( p ∧ q ) → ( q ∨ p )
วิธีทำ สมมุติว่า ( p ∧ q ) → ( q ∨ p ) เป็นเท็จ

6. การอ้างเหตุผล

การอ้างเหตุผลจะประกอบด้วยส่วนสำคัญ 2 ส่วนคือ
1. ส่วนที่เป็น เหตุ หรือ สิ่งที่กำหนดให้ ซึ่งได้แก่ P1 , P2 , P3 , … , Pn
2. ส่วนที่เป็น ผล ซึ่งได้แก่ Q

ในการอ้างเหตุผลอาจจะสมเหตุสมผล (valid) หรือไม่สมเหตุสมผล (invalid) ก็ได้ ซึ่งมีวิธีการตรวจสอบ

คือใช้ สัจนิรันดร์ โดยเชื่อมเหตุทุกเหตุด้วยตัวเชื่อม ∧ แล้ว นำเหตุกับผลมาเชื่อมด้วยตัวเชื่อม → ดังนี้