เรียนเลขออนไลน์ ฟังก์ชั่น ม.4
ความสัมพันธ์จาก A ไป B ให้ A และ B เป็นเซตใด ๆ แล้ว r เป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ AB เขียนได้ว่า
r = {(a,b) | (a,b) ∈ A×B}
กราฟของความสัมพันธ์
| ในระบบแกนมุมฉาก เราสามารถจับคู่หนึ่งต่อหนึ่ง ระหว่างคู่อันดับของจำนวนจริง (x, y) กับพิกัดของจุดบนระนาบ โดยให้ x เป็นพิกัดแรก และ y เป็นพิกัดหลัง จากหลักการดังกล่าวทำให้เราสามารถเขียนกราฟของความสัมพันธ์ได้ดังนี้ | ||
| บทนิยาม |
|
|
| ตัวอย่างที่ 1 | จงเขียนกราฟของความสัมพันธ์ |
| r = { (x,y) ∈ A × A | x + y = 5} เมื่อกำหนดให้ | |
| A = {1, 2, 3, 4}
ขั้นที่ 1 ให้ลองแทนค่าของจำนวนเต็มบวก x ลงในสมการ y = x² ที่ต้องแทน x เป็นจำนวนเต็มบวก เพราะเงื่อนไขในเซต A นั่นเอง แทน x = 1, 2, 3, 4 x = 1 ; y = 5-1 = 4 x = 2 ; y = 5-2 =3 x = 3 ; y = 5-3 = 2 x = 4 ; y = 5-4 = 1 ขั้นที่ 2 เมื่อเราแทนค่า และได้ค่า y มาแล้ว ให้เราเขียนคู่อันดับที่เราได้จากขั้นที่ 1 จะได้คู่อันดับ ดังนี้ (1, 4), (2, 3), (3, 2), (4, 1) **คู่อันดับที่ได้นี้เป็นเพียงสมาชิกบางส่วนของ r นะคะ เนื่องจากสมาชิกของ r เยอะมาก เราเลยยกตัวอย่างมาบางส่วนเพื่อที่จะเอาไปเขียนกราฟ** ขั้นที่ 3 นำคู่อันดับที่ได้จากขั้นที่ 2 มาเขียนกราฟ โดยแกนตั้งคือ y แกนนอนคือ x วิธีการเขียนกราฟคือ นำคู่อันดับแต่ละคู่มามาเขียนบนกราฟ แล้วลากเส้นเชื่อมจุดแต่ละจุด |
|
| r = {(1, 4), (2, 3), (3, 2), (4, 1)}
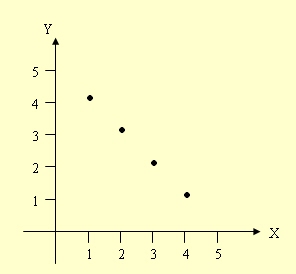 |
สมบัติของผลคูณคาร์ทีเชียน ให้ A, B และ C เป็นเซตใด ๆ และ n(A) คือ จำนวนสมาชิกของเซต A
- A×{} = {}
- {}×A = {}
- A×(B∪C) = (A×B)∪(A×C)
- A×(B∩C) = (A×B)∩(A×C)
- A×(B-C) = (A×B) – (A×C)
- n(A×B) = n(A).n(B)






