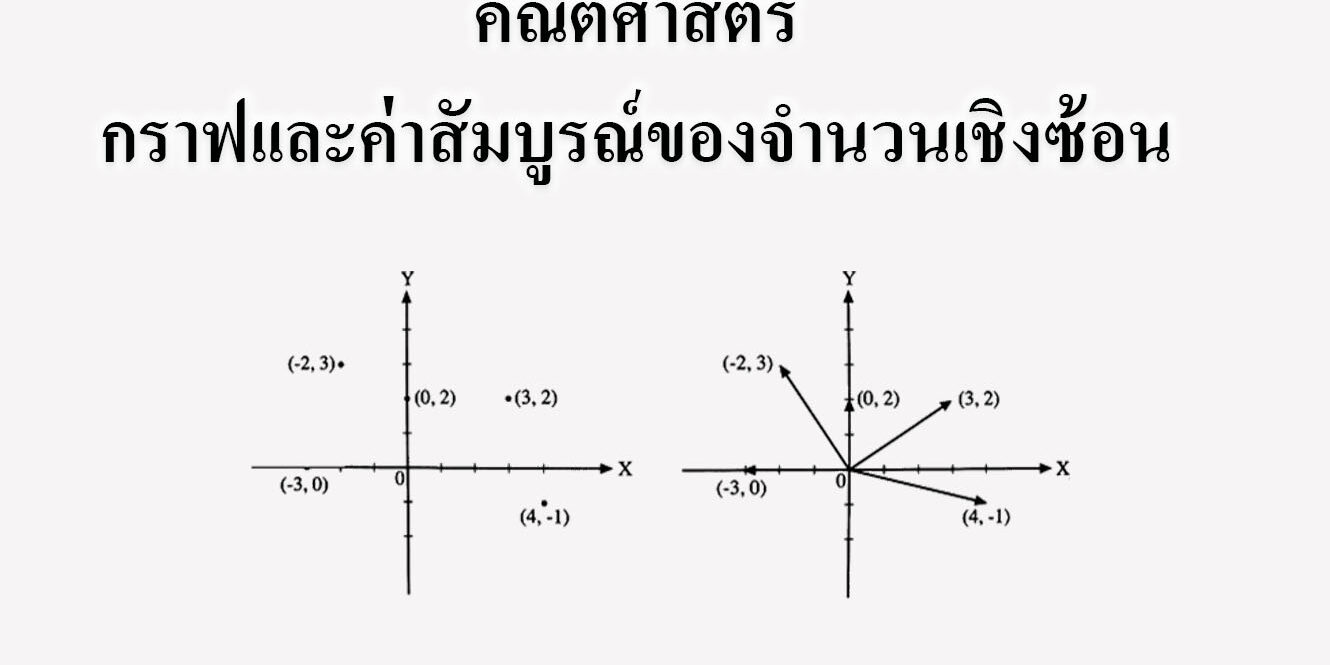
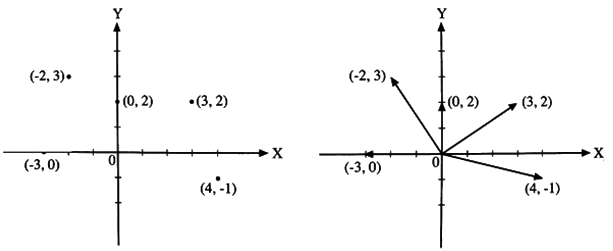
จำนวนเชิงซ้อน 3+ 2i แทนได้ด้วยจุด (3, 2) หรือแทนด้วยเวกเตอร์ที่มีจุด (0, 0) เป็นจุดเริ่มต้น และจุด (3, 2) เป็นจุดสิ้นสุด ส่วนจำนวนเชิงซ้อนอื่นๆ เช่น – 3, 2i, 4 – I, – 2+3i, แทนได้ด้วยจุดและเวกเตอร์บนระนาบเชิงซ้อนดังรูปที่ 1
ดังนั้นเราจึงได้นิยามว่า ค่าสัมบูรณ์ (absolute value หรือ modulus) ของจำนวนเชิงซ้อน a + bi คือ จำนวนจริง 
เขียนแทนด้วยสัญลักษณ์ |a + bi| จากบทนิยาม จะเห็นว่าค่าสัมบูรณ์ของ a + bi คือระยะทางระหว่างจุดกำเนิด (0, 0) กับจุด (a, b) นั่นเอง
สมบัติของค่าสัมบูรณ์
ให้ z1, z2 และ z3 เป็นจำนวนเชิงซ้อน จะได้ว่า
1. 
2. 
3. 
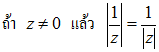
4. 
5. 
6. 
ถ้า z1 = a + bi และ z2 = c + di เป็นจำนวนเชิงซ้อน แล้ว โดยบทนิยามค่าสัมบูรณ์
หมายถึง ระยะทางระหว่างจุด (0, 0) และจุดที่แทนจำนวนเชิงซ้อน z1 – z2 ในระนาบเชิงซ้อน
z1 – z2 = (a – c) + (b – d)i
ฉะนั้น
สมบัติค่าสัมบูรณ์ มีสมบัติดังนี้
|a| ≥ 0
|a| = 0 ก็ต่อเมื่อ a = 0.
|ab| = |a | |b|
|a/b| = |a| / |b| (ถ้า b ≠ 0)
|a+b| ≤ |a| + |b| (อสมการอิงรูปสามเหลี่ยม)
|a−b| ≥ ||a| − |b||
|a| ≤ b ก็ต่อเมื่อ −b ≤ a ≤ b
|a| ≥ b ก็ต่อเมื่อ a ≤ −b หรือ b ≤ a
คุณสมบัติสองอันสุดท้าย ใช้ในการแก้อสมการอยู่เสมอ ตัวอย่างเช่น
|x − 3| ≤ 9
−9 ≤ x−3 ≤ 9
−6 ≤ x ≤ 12
“x” = [-6,12]
|x − 3| ≥ 9
x − 3 ≤ -9 U x − 3 ≥ 9
x ≤ -6 U x ≥ 12
“x” = (-infinity,-6] U [12,infinity)
