คณิตศาสตร์พื้นฐานหลักการนับเบื้องต้น ม.4
หลักการนับเบื้องต้น
3.1 หลักการบวกและหลักการคูณ
3.2 การเรียงสับเปลี่ยนเชิงเส้นของสิ่งของที่แตกต่างกันทั้งหมด
3.3 การจัดหมู่สิ่งของที่แตกต่างกันทั้งหมด
หลักการบวกและหลักการคูณ
ถ้าสามารถแบ่งการทำงานออกเป็นหลายกรณี จำนวนวิธีการทำงานทั้งหมด คือ ผลรวมของจำนวนวิธีการทำงานทุกกรณี แสดงออกมาในรูปแบบ
n1 + n2 + … + nn
ถ้าการทำงานแบ่งออกเป็นหลายขั้นตอน จำนวนวิธีการทำงานทั้งหมด คือผลคูณของจำนวนวิธีการทำงานทุกขั้นตอน แสดงออกมาในรูปแบบ
n1 ✕ n2 ✕ … ✕ nn
วิธีการเรียงสับเปลี่ยน (Permutation) คือการเรียงสิ่งของโดยคำนึงถึงตำเเหน่งของสิ่งของเเต่ละสิ่งเป็นที่สำคัญที่สุด โดยจะใช้บทนิยามที่ว่า “ถ้า n เป็นจำนวนเต็มบวก จะใช้เเฟกทอเรียล (factorial) n โดยเป็นผลคูณตั้งเเต่ 1 ถึง n เขียนเเทนด้วย n!”
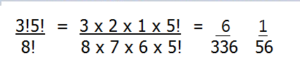
วิธีการเรียงสับเปลี่ยนเชิงเส้น
วิธีเรียงสับเปลี่ยน (Permutation)
- วิธีการเรียงสับเปลี่ยนสิ่งของที่แตกต่างกันทั้งหมด
หมายถึง การนำสิ่งของที่มีลักษณะที่แตกต่างกันทั้งหมดมาจัดเรียงสับเปลี่ยน โดยถือตำแหน่งหรือลำดับก่อนหลังเป็นสำคัญ แบ่งออกเป็น 3 แบบ คือ
1) จำนวนวิธีเรียงสับเปลี่ยนของสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนวเส้นเดียวกัน (แตไม่เป็นวงกลม) เท่ากับ n! วิธี
2) จำนวนวิธีเรียงสับเปลี่ยนสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนวเส้นเดียวกัน โดยจัดทีละ r สิ่ง (r £ n) เท่ากับ n! / (n-r)! วิธี
* เขียนแทนด้วย P(n, r) = n! / (n-r)!
จาก P(n, r) = n! / (n-r)!
= n . (n-1) . (n-2) . … . (n-r+1) . (n-r)! / (n-r)!
= n . (n-1) . (n-2) . … . (n-r+1)
การเรียงสับเปลี่ยน
ต่อเนื่องจากหลักการคูณ หากมีสิ่งของอยู่ n ชิ้นที่แตกต่างกันทั้งหมด แล้วต้องการจะนำสิ่งของ r ชิ้นจากสิ่งของที่มีอยู่ นำมาเรียงลำดับจะได้ว่า
- ขั้นตอนที่ 1 เลือกของชิ้นที่ 1 มาวาง ซึ่งจะเป็นชิ้นใดก็ได้ มี n ชิ้น
- ขั้นตอนที่ 2 เลือกของชิ้นที่ 2 มาวาง โดยเป็นชิ้นที่เหลือจากการวางชิ้นที่ 1 มี n-1 ชิ้น
- ขั้นตอนที่ r เลือกของชิ้นที่ r โดยเป็นชิ้นที่เหลือจากการวางชิ้นที่ r-1 มี n-r+1 ชิ้น
ดังนั้น จำนวนวิธีในการนำสิ่งของมาเรียง = n ✕ (n-1) ✕ (n-2) ✕ … ✕ (n-r+1)
หรือเรียกอีกอย่างว่า แฟกทอเรียล เขียนแทนด้วย n! โดยที่ n เป็นจำนวนเต็มบวก
โดย n! = n ✕ (n-1) ✕ (n-2) ✕ … ✕ 3 ✕ 2 ✕ 1
และ 0! = 1
วิธีการเรียงสับเปลี่ยนสิ่งของที่ไม่แตกต่างกันทั้งหมด
จำนวนวิธีเรียงสับเปลี่ยนของสิ่งของ n สิ่ง ซึ่งซ้ำกันบางส่วน ดังนี้
กลุ่มที่ 1 มีสิ่งของที่มีความซ้ำกันอยู่ n1 สิ่ง
กลุ่มที่ 2 มีสิ่งของที่มีความซ้ำกันอยู่ n2 สิ่ง
กลุ่มที่ 3 มีสิ่งของที่มีความซ้ำกันอยู่ n3 สิ่ง
กลุ่มที่ k มีสิ่งของที่มีความซ้ำกันอยู่ nk สิ่ง
เมื่อ n = n1 + n2 + n3 + … + nk
1) จำนวนวิธีเรียงสับเปลี่ยนของสิ่งของทั้ง n สิ่ง ซึ่งไม่แตกต่างกันทั้งหมดในแนวเส้นตรง คือ [n! / n1! . n2! . n3! . … . nk!] วิธี
2) จำนวนวิธีเรียงสับเปลี่ยนของสิ่งของทั้ง n สิ่ง ซึ่งไม่แตกต่างกันทั้งหมดในแนวเส้นตรง โดยจัดทีละ r สิ่ง (r)
2.การเรียงสับเปลี่ยนของ n สิ่ง ซึ่งมีบางสิ่งซ้ำกัน มีวิธีการจัดเรียงได้ทั้งหมด = n! วิธี
n1!n2!n3!…..nk!
วิธีการเรียงสับเปลี่ยนสิ่งของที่แตกต่างกันทั้งหมด
หมายถึง การนำสิ่งของที่มีลักษณะที่แตกต่างกันทั้งหมดมาจัดเรียงสับเปลี่ยน โดยถือตำแหน่งหรือลำดับก่อนหลังเป็นสำคัญ
แบ่งออกเป็น 3 แบบ คือ
1) จำนวนวิธีเรียงสับเปลี่ยนของสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนวเส้นเดียวกัน (แต่ไม่เป็นวงกลม) เท่ากับ n! วิธี
2) จำนวนวิธีเรียงสับเปลี่ยนสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนวเส้นเดียวกัน โดยจัดทีละ r สิ่ง (r £ n) เท่ากับ n! / (n-r)! วิธี
เขียนแทนด้วย P(n, r) = n! / (n-r)!
จาก P(n, r) = n! / (n-r)!
= n . (n-1) . (n-2) . … . (n-r+1) . (n-r)! / (n-r)!
= n . (n-1) . (n-2) . … . (n-r+1)
ตัวอย่าง จะมีวิธีการเรียงตัวอักษรในคำว่า MISSISSIPPI มาเรียงสับเปลี่ยนกันใหม่ทั้งหมดได้ กี่วิธี
วิธีทำ มีตัว S ซ้ำ 4 ตัว มีตัว I ซ้ำ 4 ตัว มีตัว P ซ้ำ 2 ตัว
มีตัว M ซ้ำ 1 ตัว
มีวิธีการเรียงสับเปลี่ยน = 11!
4! 4! 2! 1!
= 11 x 10 x 9 x7 x5
= 34,650 วิธี
3.การเรียงสับเปลี่ยนแบบวงกลม
ถ้ามีของ n สิ่งต่าง ๆ กัน นำของทั้ง n สิ่งมาเรียงสับเปลี่ยนแบบวงกลม จำนวนวิธี ที่จะจัดได้ทั้งหมด คือ (n-1)! วิธี
ถ้ามีของ n สิ่งต่าง ๆ กัน เลือกมาเรียงสับเปลี่ยนแบบวงกลมเพียง r สิ่ง (r<n) จำนวนวิธีที่จัดได้ทั้งหมด คือ n! วิธี (n-r)!r
จำนวนวิธีเรียงสับเปลี่ยนของสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนววงกลม เท่ากับ (n-1)! วิธี และมีหลักการจัดเรียงโดยแบ่งตามเงื่อนไขได้ดังนี้
3.1 การจัดสิ่งของ n สิ่ง วึ่งแตกต่างกันทั้งหมดในแนววงกลม โดยไม่มีเงื่อนไข จะจัดได้เท่ากับ (n-1)! วิธี
3.2 การสร้างจุดอ้างอิงบนวงกลมก่อน แล้วแทรกเข้าไป วนเป็นวงกลม โดยที่รู้ว่ามีจุดอ้างอิงก่อนแล้ว
3.3 การจัดสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนววงกลม โดยที่มีเงื่อนไขการสับที่ แล้วแทรกอีกฝ่ายหนึ่งเข้าในฝ่ายแรก โดยต้องรู้ว่าการแทรกครั้งนี้มีจุดอ้างอิงแล้ว
3.4 การจัดสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนววงกลม โดยจัดทีละ r สิ่ง (r £ n) เท่ากับ n! / (n-r)! . r! วิธี
เขียนแทนด้วย [P(n, r)] / r = n! / (n-r)! . r!
3.5 การจัดสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนววงกลมแบบมองได้ 2 ด้าน (แบบสามมิติ)
3.6 การจัดสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนววงกลมแบบมองได้ 2 ด้าน โดยจัดทีละ r สิ่ง (r £ n)
เขียนแทนด้วย [P(n, r)] / 2r = n! / (n-r)! . 2r!
4.การจัดหมู่( Combination)
ถ้ามีของ n สิ่งต่าง ๆ กัน เราเลือกมา r สิ่ง แบบจัดหมู่ จำนวนวิธีที่เลือกได้คือ
Cn,r = n = n!
r (n-r)!r!
r ที่สุ่มมาได้มีลักษณะคล้ายคลึงกัน
ตัวอย่าง มีหนังสือที่แตกต่างกัน 5 เล่ม ถ้าอนุญาตให้เด็กยืมได้ 3 เล่ม เด็กคนหนึ่งจะมีวิธีเลือกได้กี่วิธี
วิธีทำ หนังสือ 3 เล่มที่ยืมมาได้ถือว่ามีลักษณะไม่แตกต่างกันสลับที่กันไม่มีผลดังนั้นใช้ C 5,2 = 5! = 10 วิธี
3!2!






