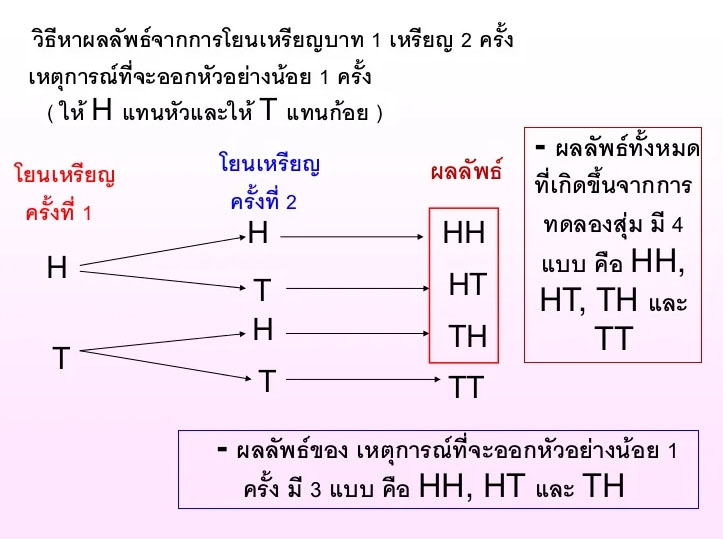
ความน่าจะเป็น โอกาสของเหตุการณ์
ความน่าจะเป็นของเหตุการณ์คือจำนวนที่แสดงให้ทราบว่าเหตุการณ์ใดเหตุการณ์หนึ่งมีโอกาสเกิดขึ้นมาก หรือน้อยเพียงใด ความน่าจะเป็นของเหตุการณ์ใด ๆ เท่ากับอัตราส่วนของจำนวนเหตุการณ์ที่เราสนใจ (จะให้เกิดขึ้นหรือไม่เกิดขึ้นก็ได้) ต่อจำนวนผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้ ซึ่งมีสูตรในการคิดคำนวณดังนี้

เมื่อผลทั้งหมดที่อาจจะเกิดขึ้นจากการทดลองสุ่มแต่ละตัวมีโอกาสเกิดขึ้นได้เท่าๆ กัน
กำหนดให้ E แทน เหตุการณ์ที่เราสนใจ
P(E) แทน ความน่าจะเป็นของเหตุการณ์
n(E) แทน จำนวนสมาชิกของเหตุการณ์
S แทน ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้
n(S) แทน จำนวนสมาชิกของผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้ ดังนั้น
![]()
คุณสมบัติของความน่าจะเป็นของเหตุการณ์
1. ความน่าจะเป็นของเหตุการณ์ใดๆ มีค่าตั้งแต่ 0 ถึง 1
2. ความน่าจะเป็นของเหตุการณ์ที่เกิดขึ้นแน่นอน เท่ากับ 1
3. ความน่าจะเป็นของเหตุการณ์ที่ไม่มีโอกาสเกิดขึ้นเท่ากับ 0
ความน่าจะเป็นกับการตัดสินใจ จากการศึกษาเรื่องความน่าจะเป็นสามารถช่วยให้เรารู้ว่าเหตุการณที่พิจารณาอยู่นั้นมีโอกาสเกิดขึ้นมากน้อยเพียงใด แต่บางเหตุการณ์ความรู้ เรื่องความน่าจะเป็นเพียงอย่างเดียวอาจไม่เพียงพอที่จะช่วยเราตัดสินใจได้ จำเป็นจะต้องหาองค์ประกอบอื่นมาช่วยในการตัดสินใจด้วยซึ่งองค์ประกอบหนึ่ง คือ ผลตอบแทนของการเกิดเหตุการณ์นั้น ในทางสถิติได้นำความน่าจะเป็นของเหตุการณ์และผลตอบแทนของการเกิดเหตุการณ์นั้น พิจารณาประกอบกันเป็นค่าคาดหมาย ซึ่งหาได้จากผลรวมของผลคูณระหว่างความน่าจะเป็น ของเหตุการณ์กับผลตอบแทนของเหตุการณ์
ในชีวิตประจำวันเราอยู่กับเหตุการณ์ต่าง ๆ และมีคำถามอยู่ในใจตลอดเวลา เช่น
– พรุ่งนี้ฝนจะตกหรือไม
– บางทีเราต้องไปทำงานวันนี้
– นายกอาจลาออกและยุปสภาเร็ว ๆ นี้
– ทีมฟุตบอลทีมใดจะได้เป็นแชมป์โลก
– ใครชนะเลือกตั้งในสมัยหน้า
คำว่า ความน่าจะเป็นหรือ probability เป็นวิธีการวัดความไม่แน่นอนในรูปแบบคณิตศาสตร
์ เช่นเมื่อโยนเหรียญความน่าจะเป็นของเหรียญที่จะออกหัวหรือก้อยเท่ากับ 0.5 ดังนั้นเหตุการณ์ต่าง ๆที่เกิดขึ้น
ในอนาคตเป็นสิ่งที่ยากจะคาดเดาได้ถูกต้องร้อยเปอร์เซ็นต์นักอุตุนิยมวิทยาจึงใช้หลักการของความน่าจะเป็นเข้ามาทำนาย
เช่น ความน่าจะเป็นของการเกิดฝนตกใน กรุงเทพมหานคร ในวันพรุ่งนี้มีค่าเท่ากับ 0.7 ความน่าจะเป็นค่าที่อาจมี
ความหมาย ที่หลายคน เข้าใจได้ไม่ยาก ความน่าจะเป็น
เป็นศาสตร์ที่มีความละเอียดอ่อนที่จะนำไปประยุกต์ใช้ โดยเฉพาะเหตุการณ์ในชีวิตประจำ วันต่าง ๆ
ความน่าจะเป็นมีการกำหนดค่าเป็นเศษส่วนหรือเป็นเปอร์เซ็นต์หรือให้มีค่าระหว่างถึงเช่น ถ้านำลูกเต๋า ทอยลงบนพื้นโอกาสที่จะปรากฎหน้ามีค่าเท่ากับเปอร์เซนต์ ถ้าโยนเหรียญหนึ่งเหรียญ และให้ตกบนพื้น (โยนแบบยุติธรรม) โอกาสที่จะปรากฏหัวเท่ากับหรือ
ในทางคณิตศาสตร์ เราหา ค่าของความน่าจะเป็นของเหตุการณ์ซึ่ง ไม่ทราบแน่ว่าจะเกิดหรือไม่ได้ โดยพิจารณา น้ำหนัก ที่เหตุการณ์นั้นๆ จะเกิด ถ้ากำหนดให้น้ำหนักของเหตุการณ์ที่เกิดขึ้นไม่ได้มีค่าเป็น 0 น้ำหนัก ของ เหตุการณ์ที่เกิดขึ้นแน่มีค่าเป็น1และน้ำหนักของเหตุการณ์ใด ๆ ที่อาจ เกิดขึ้นมีค่าเป็นจำนวนเลขที่อยู่ระหว่าง0 กับ 1 เราจะมีตัวเลขมากมายนับ ไม่ถ้วน แสดงค่าของน้ำหนัก หรือโอกาสที่เหตุการณ์ต่าง ๆ จะเกิดขึ้นได และเรียกค่าของน้ำหนัก นี้ว่า
ค่าของความน่าจะเป็น

พิจารณาการโยนเหรียญบาทหนึ่งเหรียญ ถ้าเหรียญนั้นไม่ได้มีการถ่วง ให้หน้าใดง่ายง่ายกว่าหน้าอื่นก็เชื่อว่า
“น้ำหนัก” ของการที่เหรียญจะ หงายหน้าใดหน้าหนึ่งย่อมเท่ากัน
ผลที่เป็นไปได้ทั้งหมดมี 2 อย่าง
คือเหรียญหงายหัวหรือเหรียญหงายก้อยซึ่งอาจเกิดอย่างใดอย่างหนึ่งได้เท่าๆกัน
ผลที่เป็นไปได้ทั้งหมดมี 2 อย่าง
โอกาสที่เหรียญจะหงายหัว = 1/2
โอกาสที่เหรียญจะหงายหัว = 1/2
เรากล่าวว่า ความน่าจะเป็นที่เหรียญหงายหัวมีค่า 1/2
และความน่าจะเป็นที่เหรียญหงายก้อยมีค่า 1/2

ในการทอดลูกเต๋าลูกหนึ่ง เมื่อลูกเต๋านั้น ๆ มีหน้าใหญ่เท่า ๆกัน และไม่มีการถ่วงให้หน้าใดหงายง่ายกว่าหน้าอื่น
ก็เชื่อได้ว่า “น้ำหนัก” ของการที่ลูกเต๋าจะหงายหน้าใดหน้าหนึ่งย่อมเท่ากัน
ผลที่ลูกเต๋าจะขึ้นหน้าต่าง ๆ ทั้งหมดมี 6 อย่าง คือ อาจขึ้นหน้า หนึ่ง สอง สาม สี่ ห้า หรือหก ด้วยความน่าจะเป็น เท่า ๆ กัน คือ 1/6

พิจารณาการโยนเหรียญบาทหนึ่งเหรียญ และเหรียญห้าบาทหนึ่งเหรียญ พร้อม ๆ กัน เหรียญย่อมหงายได้ 4
อย่าง ความน่าจะเป็นที่เหรียญใดจะหงายหัวหรือก้อยมีเท่า ๆ กัน คือ 1/2 สำหรับ แต่ละเหรียญ
เราใช้ทฤษฎีของความน่าจะเป็นคำนวณค่าของความน่าจะเป็น ได้ดังนี้
ความน่าจะเป็นที่เหรียญทั้งสองจะหงายหัว = 1/4
ความน่าจะเป็นที่เหรียญทั้งสองจะหงายก้อย = 1/4
ความน่าจะเป็นที่เหรียญหนึ่งหงายหัวกับอีก เหรียญหนึ่งหงายก้อย = 1/2
นอกจากเรื่องโยนลูกเต๋า โยนเหรียญ จับสลาก แจกไพ่แล้ว ยัง มีเรื่องอื่น ๆ อีกมาก ที่มีผลการเกิดซึ่งบอกล่วงหน้าไม่ได้ว่าจะให้ผลอย่างไรทางคณิตศาสตร์จึงต้องใช้สัญลักษณ์มาช่วยจำลองเหตุการณ์ต่างๆ
ที่อาจ เกิดขึ้นเฉพาะเรื่อง
และอาศัยกฎเกณฑ์ของคณิตศาสตร์ในแขนงอื่น ๆ ทำให้ เกิดทฤษฎีต่าง ๆ ที่สามารถนำไปหาค่าความน่าจะเป็นของเรื่องที่เกี่ยวข้อง กับความไม่แน่นอนทั้งหลายได และสามารถใช้ค่าเหล่านี้คำนวณหาค่าอื่น ๆ ที่จะเป็นประโยชน์ในการนำไปใช้ประกอบการตัดสินใจ เช่น ใช้ค่าของความน่าจะเป็นที่จะมีลูกค้าเข้ามาซื้อของในร้าน เพื่อหาว่าโดยเฉลี่ยจะ มีลูกค้าเข้ามาซื้อของกี่คน นักคณิตศาสตร์ชาวฝรั่งเศส เป็นผู้ให้กำเนิดเรื่องของความน่าจะเป็น เมื่อประมาณ 300 ปีมาแล้ว แต่เพิ่งจะได้มีการศึกษาโดยละเอียดและนำไปใช้เมื่อประมาณ 40 ปีมานี้เอง ปัจจุบัน เรื่องราวของความน่าจะเป็น มีความสำคัญอย่างมาก การค้นคว้า การวิจัย และการปฏิบัติงานใด ๆ ที่ เกี่ยวข้องกับการคาดคะเน จะต้องอาศัยเรื่องของความน่าจะเป็นทั้งสิ้น เช่น การเกษตร การแพทย์ เศรษฐศาสตร์ วิทยาศาสตร์และเทคโน โลยีทุกสาขา ความน่าจะเป็นบางเรื่องใช้คณิตศาสตร์ชั้นสูงหลายวิชามาเกี่ยว โยงกัน และยังมีเรื่องต้องศึกษาค้นคว้าอีกมาก
ในทางคณิตศาสตร์มักเขียนแสดงความน่าจะเป็นของเหตุการณ์ต่างๆในลักษณะนี้
P(ได้เลขคี่)=P({1,3,5})=3/6
P(ได้มากกว่า3)=P({4,5,6})=4/6
P(ได้2ขึ้นไป)=P({2,3,4,5,6})=5/6
วิธีเขียนเป็น P(เงื่อนไข) = ค่าความน่าจะเป็น แบบนี้เป็นหลักสากลที่ใช้กันทั่วไป บางที่อาจเขียน p() ตัวพิมพ์เล็ก หรือเขียนเป็น Pr() หรือ Prob() ก็มี แต่ส่วนใหญ่จะเขียนเป็น P() แบบนี้ ในบทความนี้เองก็จะเขียนแบบนี้ตลอดด้วย
ส่วนกรณีของการทอยลูกเต๋าซึ่งโดยทั่วไปมี 6 หน้า
โอกาสออกแต่ละหน้าเท่ากันก็ควรจะเป็นแบบนี้
P(ได้1)=1/10
P(ได้2)=4/10
P(ได้3)=1/10
P(ได้4)=1/10
P(ได้5)=2/10
P(ได้6)=1/10

นอกจากนี้ยังอาจพิจารณาเหตุการณ์ต่างๆที่รวมถึงหลายหน้าพร้อมกันเช่น
- ได้เลขคี่: คือได้ 1,3,5
- ได้มากกว่า 3: คือได้ 4,5,6
- ได้ 2 ขึ้นไป: คือได้ 2,3,4,5,6
อาจเขียนสมาชิกของเหตุการณ์ในรูปของเซ็ต เช่น {1,3,5}, {4,5,6}, {2,3,4,5,6} แบบนี้
ความน่าจะเป็นของเหตุการณ์เหล่านี้ก็จะเป็น
ยิ่งไปกว่านั้น บางทีโลกนี้ก็อาจไม่ได้เรียบง่ายแบบนั้น เช่นถ้ามีใครใช้วิธีการอะไรบางอย่างทำให้หน้าเหรียญหน้าหนึ่งมีโอกาสออกมากกว่าอีกหน้า เช่นโอกาสออกหัวเหลือแค่ 2/5 ออกก้อย 3/5

ลูกเต๋าเองก็อาจมีการเล่นตุกติกให้บางหน้ามีโอกาสออกมากว่าหน้าอื่น เช่นความน่าจะเป็นกลายเป็นแบบนี้

ถ้าเป็นแบบนี้ ความน่าจะเป็นของเหตุการณ์เหล่านี้ก็ต้องเปลี่ยนไป โดยรวมจากพื้นที่ที่แบ่งแบบใหม่นี้
จะเห็นได้ว่าเมื่อเทียบความน่าจะเป็นเป็นการแบ่งพื้นที่แล้วจะช่วยให้นึกภาพได้เข้าใจได้ง่ายขึ้น
เมื่อผลทั้งหมดที่อาจจะเกิดขึ้นจากการทดลองสุ่มแต่ละตัวมีโอกาสเกิดขึ้นได้เท่าๆ กัน
กำหนดให้ E แทน เหตุการณ์ที่เราสนใจ
P(E) แทน ความน่าจะเป็นของเหตุการณ์
n(E) แทน จำนวนสมาชิกของเหตุการณ์
S แทน ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้
n(S) แทน จำนวนสมาชิกของผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้ ดังนั้น
คุณสมบัติของโอกาศของเหตุการณ์
1. โอกาศของเหตุการณ์ใดๆ มีค่าตั้งแต่ 0 ถึง 1
2. โอกาสของเหตุการณ์ที่เกิดขึ้นแน่นอน เท่ากับ 1
3. ความโอกาสของเหตุการณ์ที่ไม่มีโอกาสเกิดขึ้นเท่ากับ 0
ความน่าจะเป็นกับการตัดสินใจ จากการศึกษาเรื่องความน่าจะเป็นสามารถช่วยให้เรารู้ว่าเหตุการณที่พิจารณาอยู่นั้นมีโอกาสเกิดขึ้นมากน้อยเพียงใด แต่บางเหตุการณ์ความรู้ เรื่องความน่าจะเป็นเพียงอย่างเดียวอาจไม่เพียงพอที่จะช่วยเราตัดสินใจได้ จำเป็นจะต้องหาองค์ประกอบอื่นมาช่วยในการตัดสินใจด้วยซึ่งองค์ประกอบหนึ่ง คือ ผลตอบแทนของการเกิดเหตุการณ์นั้น ในทางสถิติได้นำความน่าจะเป็นของเหตุการณ์และผลตอบแทนของการเกิดเหตุการณ์นั้น พิจารณาประกอบกันเป็นค่าคาดหมาย ซึ่งหาได้จากผลรวมของผลคูณระหว่างความน่าจะเป็น ของเหตุการณ์กับผลตอบแทนของเหตุการณ์
ในชีวิตประจำวันเราอยู่กับเหตุการณ์ต่าง ๆ และมีคำถามอยู่ในใจตลอดเวลา เช่น
– พรุ่งนี้ฝนจะตกหรือไม
– บางทีเราต้องไปทำงานวันนี้
– นายกอาจลาออกและยุปสภาเร็ว ๆ นี้
– ทีมฟุตบอลทีมใดจะได้เป็นแชมป์โลก
– ใครชนะเลือกตั้งในสมัยหน้า
คำว่า ความน่าจะเป็นหรือ probability เป็นวิธีการวัดความไม่แน่นอนในรูปแบบคณิตศาสตร
์ เช่นเมื่อโยนเหรียญความน่าจะเป็นของเหรียญที่จะออกหัวหรือก้อยเท่ากับ 0.5 ดังนั้นเหตุการณ์ต่าง ๆที่เกิดขึ้น
ในอนาคตเป็นสิ่งที่ยากจะคาดเดาได้ถูกต้องร้อยเปอร์เซ็นต์นักอุตุนิยมวิทยาจึงใช้หลักการของความน่าจะเป็นเข้ามาทำนาย
เช่น โอกาสของการเกิดฝนตกใน กรุงเทพมหานคร ในวันพรุ่งนี้มีค่าเท่ากับ 0.7 ความน่าจะเป็นค่าที่อาจมี
ความหมาย ที่หลายคน เข้าใจได้ไม่ยาก ความน่าจะเป็น
เป็นศาสตร์ที่มีความละเอียดอ่อนที่จะนำไปประยุกต์ใช้ โดยเฉพาะเหตุการณ์ในชีวิตประจำ วันต่าง ๆ
ความน่าจะเป็นมีการกำหนดค่าเป็นเศษส่วนหรือเป็นเปอร์เซ็นต์หรือให้มีค่าระหว่างถึงเช่น ถ้านำลูกเต๋า ทอยลงบนพื้นโอกาสที่จะปรากฎหน้ามีค่าเท่ากับเปอร์เซนต์ ถ้าโยนเหรียญหนึ่งเหรียญ และให้ตกบนพื้น (โยนแบบยุติธรรม) โอกาสที่จะปรากฏหัวเท่ากับหรือ
ในทางคณิตศาสตร์ เราหา ค่าของความน่าจะเป็นของเหตุการณ์ซึ่ง ไม่ทราบแน่ว่าจะเกิดหรือไม่ได้ โดยพิจารณา น้ำหนัก ที่เหตุการณ์นั้นๆ จะเกิด ถ้ากำหนดให้น้ำหนักของเหตุการณ์ที่เกิดขึ้นไม่ได้มีค่าเป็น 0 น้ำหนัก ของ เหตุการณ์ที่เกิดขึ้นแน่มีค่าเป็น1และน้ำหนักของเหตุการณ์ใด ๆ ที่อาจ เกิดขึ้นมีค่าเป็นจำนวนเลขที่อยู่ระหว่าง0 กับ 1 เราจะมีตัวเลขมากมายนับ ไม่ถ้วน แสดงค่าของน้ำหนัก หรือโอกาสที่เหตุการณ์ต่าง ๆ จะเกิดขึ้นได และเรียกค่าของน้ำหนัก นี้ว่า ค่าของความน่าจะเป็น
โจทย์ตัวอย่าง
พิจารณาการโยนเหรียญบาทหนึ่งเหรียญ ถ้าเหรียญนั้นไม่ได้มีการถ่วง ให้หน้าใดง่ายง่ายกว่าหน้าอื่นก็เชื่อว่า
“น้ำหนัก” ของการที่เหรียญจะ หงายหน้าใดหน้าหนึ่งย่อมเท่ากัน
ผลที่เป็นไปได้ทั้งหมดมี 2 อย่าง
คือเหรียญหงายหัวหรือเหรียญหงายก้อยซึ่งอาจเกิดอย่างใดอย่างหนึ่งได้เท่าๆกัน
ผลที่เป็นไปได้ทั้งหมดมี 2 อย่าง
โอกาสที่เหรียญจะหงายหัว = 1/2
โอกาสที่เหรียญจะหงายหัว = 1/2
เรากล่าวว่า ความน่าจะเป็นที่เหรียญหงายหัวมีค่า 1/2
และความน่าจะเป็นที่เหรียญหงายก้อยมีค่า 1/2