ตัวประกอบและการหาตัวประกอบ

ตัวประกอบของจำนวนนับใดๆ คือ จำนวนนับที่หารจำนวนนับนั้นได้ลงตัว
เช่น a เป็นตัวประกอบของ b ก็ต่อเมื่อ b หารด้วย a ลงตัว หรือกล่าวอีกนัยหนึ่งก็คือ a หาร b ลงตัว
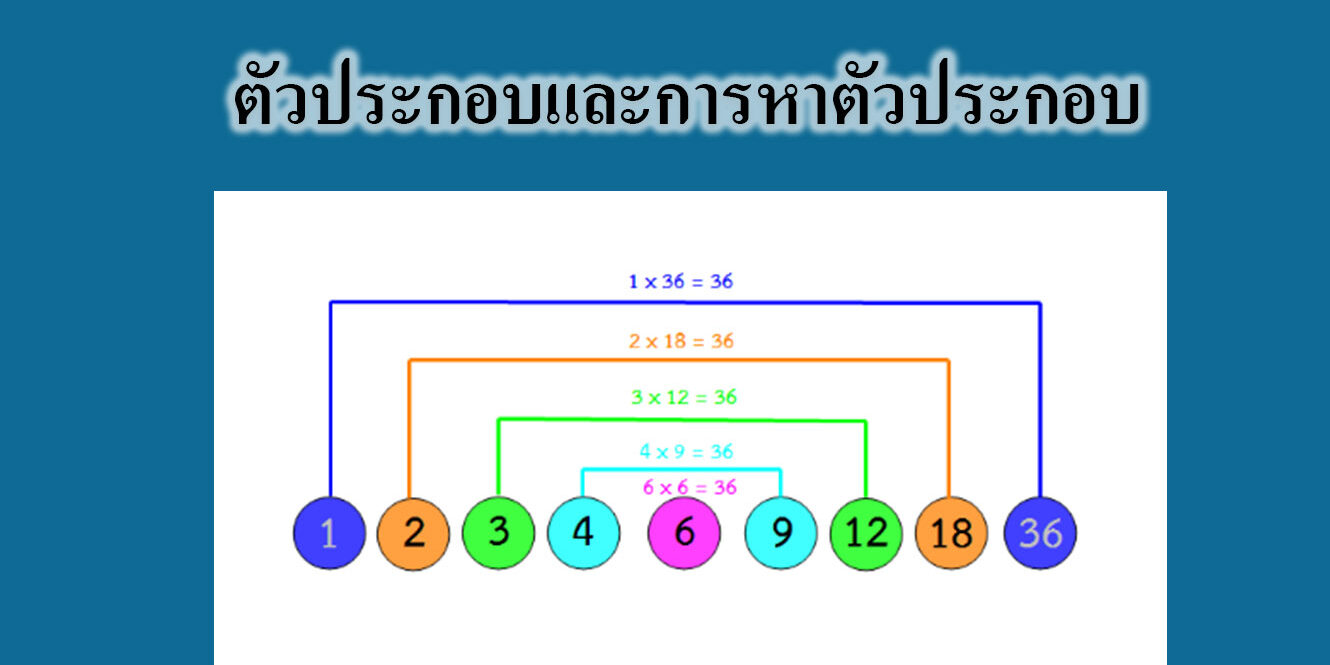
ตัวอย่าง 1 จงหาตัวประกอบทั้งหมดของ 36
วิธีทำ ให้นำจำนวนนับตั้งแต่ 1 ไปหาร 36 จำนวนนับตัวใดหาร 36 ลงตัว
จำนวนนับนั้นและผลลัพธ์ที่ได้จากการหารจะเป็นตัวประกอบของ 36 เช่น
1 ) 36 ==> จะได้ 1 และ 36 เป็นตัวประกอบของ 36
36
2 ) 36 ==> จะได้ 2 และ 18 เป็นตัวประกอบของ 36
18
3 ) 36 ==> จะได้ 3 และ 12 เป็นตัวประกอบของ 36
12
4 ) 36 ==> จะได้ 4 และ 9 เป็นตัวประกอบของ 36
9
6 ) 36 ==> จะได้ 6 เป็นตัวประกอบของ 36
6
ดังนั้น ตัวประกอบทั้งหมดของ 36 ได้แก่ 1 และ 36 , 2 และ 18 , 3 และ 12 , 4 และ 9 , 6 และ 6 (ใช้ 6 ตัวเดียว)
จะได้ ตัวประกอบทั้งหมดของ 36 คือ 1, 2, 3, 4, 6, 9, 12, 18, 36 ตอบ.
ตัวอย่าง 2 จงหาตัวประกอบทั้งหมดของ 144
จะได้ ตัวประกอบทั้งหมดของ 144 คือ 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72 และ 144 ตอบ.
ตัวอย่าง 3 จงหาตัวประกอบทั้งหมดของ 56
จะได้ ตัวประกอบทั้งหมดของ 56 คือ 1, 2, 4, 7, 8, 14, 28 และ 56 ตอบ.
ข้อสังเกต จำนวนนับทุกจำนวนจะมีตัวประกอบอย่างน้อย 2 ตัว (สังเกต สีชมพู) คือ 1 และตัวมันเอง โดยที่ 1 เป็นตัวประกอบตัวแรกและตัวมันเองเป็นตัวประกอบตัวสุดท้าย
การหาจำนวนตัวประกอบทั้งหมดของจำนวนนับ
1. แยกตัวประกอบของจำนวนนับนั้น และเขียนในรูปเลขยกกำลัง
2. ให้นำ 1 ไปบวกกับเลขชี้กำลังของแต่ละตัวของเลขยกกำลัง
3. นำผลบวกของเลขชี้กำลังที่ได้ มาคูณกัน
ตัวอย่าง 1 จงหาจำนวนของตัวประกอบทั้งหมดของ 50
50 = 2 x 5 x 5 = 21 x 52
นำ 1 ไปบวกกับเลขชี้กำลังของแต่ละตัวของเลขยกกำลัง ดังนี้
21 จะได้ 1 + 1 = 2
52 จะได้ 2 + 1 = 3
ดังนั้น ตัวประกอบทั้งหมดของ 50 มี 2 x 3 = 6 จำนวน ตอบ.
ตัวอย่าง 2 จงหาจำนวนของตัวประกอบทั้งหมดของ 144
144 = 2 x 2 x 2 x 2 x 3 x 3 = 24 x 32
นำ 1 ไปบวกกับเลขชี้กำลังของแต่ละตัวของเลขยกกำลัง ดังนี้
24 จะได้ 4 + 1 = 5
32 จะได้ 2 + 1 = 3
ดังนั้น ตัวประกอบทั้งหมดของ 50 มี 5 x 3 = 15 จำนวน ตอบ.