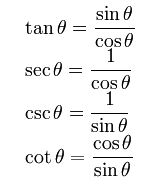อัตราส่วนตรีโกณมิติ ม.ต้น (Trigonometry Ratios)

1. ความหมายของตรีโกณมิติ
ตรีโกณมิติหมายถึง วิทยาศาสตร์วิเคราะห์(Analytic Science) จุดเริ่มตน้ของวิชาน้ีเริ่มในศตวรรษที่ 17หลังจากได้พัฒนาสัญลักษณ์ของพีชคณิตตรีโกณมิติหมายถึง เรขาคณิตที่เกี่ยวก ับดาราศาสตร์ซึ่งเกี่ยวกับการวัดมุม ต้นก าเนิดวิชานี้ อาจจะขั้นอยทที่ผลงานของ ฮิปพาร์คัส (Hipparchus)ตรีโกณมิติหมายถึงการวัดรูปสามเหลี่ยมต้นก าเนิดวิชาน้ีอาจมีมานานราว 2,000 ปี ก่อนคริสต์ศักราช
2. อัตราส่วนรูปสามเหลียม ชาวอียิปต์โบราณทำการวัดฐานของพีระมิดโดยการแบ่งเส้นเชือกออกเป็น 12 ส่วนเท่าๆกัน แล้วทำ
เชือกให้เป็นปมตรงส่วนที่แบ่งน้ัน แล้วดึงให้ตึงเป็ นรูปสามเหลี่ยม ด้วยอัตราส่วนของด้าน 3 : 4 : 5 และมุมที่อยู่ ตรงข้ามกับด้านที่ยาวที่สุดจะเป็ นมุมฉากเสมอ จึงเป็ นที่น่าเชื่อได้ว่าทฤษฎีปี ทาโกรัสเป็นที่รู้จักกันมาแพร่หลายแล้ว

อัตราส่วนตรีโกณมิติ (TRIGONOMETRY RATIOS)

1.ฟังก์ชันไซน์และโคไซน์

การกำหนดค่าของฟังก์ชันตรีโกณมิตินั้น สามารถทำได้โดยการใช้วงกลมรัศมี 1 หน่วย มีจุดศูนย์กลางอยู่ที่จุดกำเนิด

และเราจะเรียกวงกลมดังกล่าวว่า วงกลมหนึ่งหน่วย (The unit circle)

เมื่อเรากำหนดจำนวนจริง θ (ทีตา) จาก (1,0) วัดระยะไปตามส่วนโค้งของวงกลม โดยมีข้อตกลงดังนี้ว่า :

ถ้า θ > 0 จะวัดส่วนโค้งจากจุด (1,0) ไปในทิศทางทวนเข็มนาฬิกา

ถ้า θ < 0 จะวัดส่วนโค้งจากจุด (1,0) ไปในทิศทางตามเข็มนาฬิกา

ถ้า θ = 0 จุดปลายส่วนโค้งคือจุด (1,0)

จะได้ว่า เมื่อเรากำหนดจำนวนจริง θ ให้ เราสามรารถหาจุด (x,y) ซึ่งเป็นจุดปลายส่วนโค้งได้เพียงจุดเดียวเท่านั้น

ถ้า |θ| > 2π แสดงว่า วัดส่วนโค้งเกิน 1 รอบ เพราะเส้นรองวงของวงกลมยาว 2π หน่วย

เมื่อ (x,y) เป็นจุดปลายส่วนโค้งของวงกลมข้างต้น

y = sinθ (อ่านว่า วาย เท่ากับ ไซน์ทีตา)

x = cosθ (อ่านว่า เอกซ์ เท่ากับ คอสทีตา)

ฟังก์ชันไซน์และฟังก์ชันโคไซน์นั้น เป็นจำนวนจริง ตั้งแต่ -1 ถึง 1

นั่นคือ เรนจ์ของฟังก์ชันไซน์และโคไซน์ คือ เซตของจำนวนจริง ตั้งแต่ -1 ถึง 1

และโดเมนของฟังก์ชันทั้งสองคือเซตของจำนวนจริง

2.ค่าของฟังก์ชันไซน์และโคไซน์

ค่าของฟังก์ชันไซน์และโคไซน์ เป็นดังตารางนี้

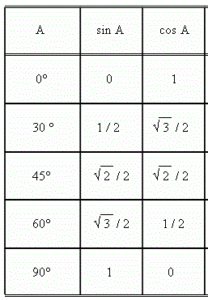
จากตาราง ทำให้เราสามารถสรุปได้ว่า

sin(-θ) = -sinθ

cos(-θ) = cosθ