เรียนคณิตศาสตร์ เรื่อง Set เซต ม.4 – เพาเวอร์เซต(Power Set) 

การหาสับเซตทั้งหมดของA

จำนวนสับเซตทั้งหมดหาได้จาก 2ⁿ เมื่อ n = จำนวนสมาชิกในเซต

ตัวอย่าง             จงหาสับเซตทั้งหมดของ A เมื่อ A = {2, 4, 6, 8}

A จะมีสับเซตทั้งหมด 2⁴ =16 สับเซต เมื่อแจกแจงสับเซตทั้งหมดจะได้ดังนี้

Ø

{2}  {4}  {6}  {8}

{2, 4}  {2, 6}  {2, 8}  {4, 6}  {4, 8}  {6, 8}

{2, 4, 6}  {2, 6, 8}  {2, 4, 8}  {4, 6, 8}

{2, 4, 6, 8}

ความหมายของสับเซตแท้

สับเซตแท้ คือ สับเซตทั้งหมดที่ไม่ใช่ตัวมันเอง มี 2ⁿ – 1 สับเซต (เซตว่างไม่มีสับเซตแท้)

นิยาม A เป็นสับเซตแท้ของ B ก็ต่อเมื่อ A⊂B และ A ≠ B

ซึ่งจะได้รูปดังภาพ

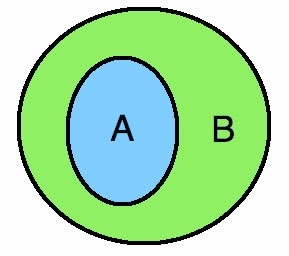
การหาจำนวนสับเซตทั้งหมดของ A

            หลักในการเขียนสับเซตทั้งหมดของเซตๆหนึ่งที่โจทย์กำหนดมาทำโดย เริ่มเขียนตั้งแต่เซตว่าง แล้วตามด้วยเซตที่มีสมาชิก 1 ตัว, 2 ตัว ไปเรื่อยๆ จนมีสมาชิกเท่ากับเซตที่โจทย์กำหนดมา (ตัวมันเอง) โดยสมาชิกที่นำมาใช้เขียนต้องเป็นสมาชิกของเซตที่โจทย์กำหนดมาด้วย

ตัวอย่าง  จงเขียนสับเซตทั้งหมดของเซตต่อไปนี้

1. A = Ø สับเซตทั้งหมดของ A มี 1 สับเซต คือ Ø

2. B = {1} สับเซตทั้งหมดของ B มี 2 สับเซต คือ 1) Ø   2) {1}

3. C = {1,3} สับเซตทั้งหมดของ C มี 4สับเซต คือ  1) Ø   2) {1}  3) {3}   4) {1,3}

4. D = {1,3,5} สับเซตทั้งหมดของ D มี 4 สับเซต คือ1) Ø   2) {1}   3) {3}   4) {5}   5) {1,3}   6)  

   {1,5}   7) {3,5}   8) { 1,3,5}