เรียนเลขออนไลน์ ตรีโกณมิติ ม.5
ตรีโกณมิติ sin cos tan
หากน้องๆ จำได้ ใน ม.3 ที่เราเรียนกันในอัตราส่วนตรีโกณมิติ sin cos tan ที่เราท่องหรือร้องเพลงกันว่า ”sin คือ ข้ามฉาก cos คือ ชิดฉาก tan คือ ข้ามชิด” อันนี้เป็นการประยุกต์ใช้ sin cos tan แบบง่ายกับสามเหลี่ยมมุมฉาก
ใน ตรีโกณมิติ ม.5 เราจะมาหาค่า sin cos tan แบบเยอะมุมมากขึ้น อย่างเช่น มุมที่มากกว่า 90 องศา ไปจนถึง มุมที่มากกว่า 360 องศา หรือมุมอื่นๆ ทั่วไป โดยการใช้ ”วงกลมหนึ่งหน่วย”
การจดจำค่าของฟังก์ชันตรีโกณมิติ โดยมีฟังก์ชันพื้นฐานอยู่ 3 ฟังก์ชัน ซึ่งเป็นค่าของแต่ละด้านที่หารด้วยอีกด้านหนึ่ง ได้แก่
***sine***
sin θ = ด้านตรงข้ามมุม θ/ด้านตรงข้ามมุมฉาก
= ข้าม/ฉาก
***cosine***
cos θ = ด้านประชิดมุม θ/ด้านตรงข้ามมุมฉาก
= ชิด/ฉาก
***tangent***
tan θ = ด้านตรงข้ามมุม θ/ด้านประชิดมุม θ
= ข้าม/ชิด

นิยามด้วยวงกลมหนึ่งหน่วย
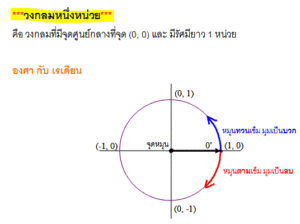
วงกลมหนึ่งหน่วย
ฟังก์ชันตรีโกณมิติทั้ง 6 ฟังก์ชัน สามารถนิยามด้วยวงกลมหนึ่งหน่วย ซึ่งเป็นวงกลมที่ มีรัศมียาว 1 หน่วย และมีจุดศูนย์กลางอยู่ที่จุดกำเนิด วงกลมหนึ่งหน่วยช่วยในการคำนวณ และหาค่าฟังก์ชันตรีโกณมิติสำหรับอาร์กิวเมนต์ที่เป็นบวกและลบได้ ไม่ใช่แค่ 0 ถึง π/2 เรเดียนเท่านั้น สมการของวงกลมหนึ่งหน่วยคือ:
จากรูป เราจะวัดมุมในหน่วยเรเดียน โดยให้มุมเป็นบวกในทิศทวนเข็มนาฬิกา และมุมเป็นลบในทิศตามเข็มนาฬิกา ลากเส้นให้ทำมุม θ กับแกน x ด้านบวก และตัดกับวงกลมหนึ่งหน่วย จะได้ว่าพิกัด xและ y ของจุดตัดนี้จะเท่ากับ cos θ และ sin θ ตามลำดับ เหตุผลเพราะว่ารูปสามเหลี่ยมที่เกิดขึ้นนั้น จะมีความยาวด้านตรงข้ามมุมฉาก ยาวเท่ากับรัศมีวงกลม นั่นคือยาวเท่ากับ 1 หน่วย เราจะได้ sin θ =y/1 และ cos θ = x/1 วงกลมหนึ่งหน่วยช่วยให้เราหากรณีที่สามเหลี่ยมมีความสูงเป็นอนันต์ (เช่น มุม π/2 เรเดียน) โดยการเปลี่ยนความยาวของด้านประกอบมุมฉาก แต่ด้านตรงข้ามมุมฉากยังยาวเท่ากับ 1 หน่วย เท่าเดิม
ฟังก์ชัน f(x) = sin(x) และ f(x) = cos(x) ที่วาดบนระนาบคาร์ทีเซียน
สำหรับมุมที่มากกว่า 2π หรือต่ำกว่า −2π เราสามารถวัดมุมได้ในวงกลม ด้วยวิธีนี้ ค่าไซน์และโคไซน์จึงเป็นฟังก์ชันเป็นคาบที่มีคาบเท่ากับ 2π:
จากข้างบนนี้ ค่าไซน์และโคไซน์ถูกนิยามจากวงกลมหนึ่งหน่วยโดยตรง แต่สี่ฟังก์ชันตรีโกณมิติที่เหลือจะถูกนิยามโดย









