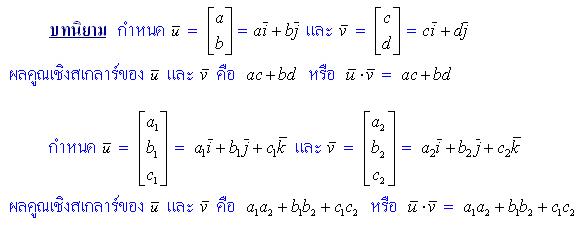เวกเตอร์คืออะไร

เวกเตอร์ (Vector) ในกรณีที่ง่ายที่สุดคือวัตถุทางคณิตศาสตร์ที่มีขนาดและทิศทาง ตัวอย่างเช่นในรูปทรงเรขาคณิตและในวิทยาศาสตร์ธรรมชาติเวกเตอร์เป็นส่วนกำกับของเส้นตรงในปริภูมิแบบยุคลิด (หรือบนระนาบ)

สามารถให้คำจำกัดความอื่นได้ ฟังก์ชันคือการดำเนินการเฉพาะกับตัวแปร ซึ่งหมายความว่าเรารับค่าของ x ทำการกระทำบางอย่างกับมัน (เช่นยกกำลังสองหรือคำนวณลอการิทึมของมัน) – และเราจะได้ค่าของ y

ตัวอย่าง: เวกเตอร์รัศมีความเร็วโมเมนต์ของแรง หากระบุระบบพิกัดในอวกาศเวกเตอร์จะถูกกำหนดโดยไม่ซ้ำกันโดยชุดพิกัดของมัน ดังนั้นในวิชาคณิตศาสตร์วิทยาการคอมพิวเตอร์และวิทยาศาสตร์อื่น ๆ ชุดตัวเลขที่เรียงตามลำดับจึงมักเรียกว่าเวกเตอร์ ในความหมายทั่วไปเวกเตอร์ในคณิตศาสตร์ถือเป็นองค์ประกอบของปริภูมิเวกเตอร์ (เชิงเส้น) บางส่วน

เป็นแนวคิดพื้นฐานอย่างหนึ่งของพีชคณิตเชิงเส้น การใช้คำจำกัดความทั่วไปที่สุดเวกเตอร์กลายเป็นวัตถุทั้งหมดที่ศึกษาในพีชคณิตเชิงเส้นรวมถึงเมทริกซ์เทนเซอร์อย่างไรก็ตามหากวัตถุเหล่านี้มีอยู่ในบริบทโดยรอบเวกเตอร์จะถูกเข้าใจว่าหมายถึงเวกเตอร์แถวหรือเวกเตอร์คอลัมน์ a เทนเซอร์ของอันดับแรกตามลำดับ มีการศึกษาคุณสมบัติของการดำเนินการกับเวกเตอร์ในแคลคูลัสเวกเตอร์

เวกเตอร์ (vector)

เวกเตอร์ เป็นปริมาณทางกายภาพที่บอกทั้งขนาดและทิศทาง ตัวอย่างปริมาณเวกเตอร์ได้แก่ การกระจัด ความเร็ว ความเร่ง และแรง ในบทนี้จะศึกษาพีชคณิตเวกเตอร์ การรวมเวกเตอร์ การคูณเวกเตอร์ นักศึกษาจึง
จําเป็นต้องทําความเข้าใจในเรื่องดังกล่าว ไม่ว่าจะเป็นการวิเคราะห์เวกเตอร์เชิงกราฟ วิเคราะห์เชิงพีชคณิต และ การคูณเวกเตอร์
1.1 พีชคณิตเวกเตอร์ (Vectors algebra) ในทางฟิสิกส์และวิศวกรรมศาสตร์นั้นการทราบจํานวนและหน่วยของปริมาณใดปริมาณหนึ่งจะไม่เพียงพอ สําหรับอธิบายปริมาณนั้น ๆ ให้สมบูรณ์ได้เช่น การเดินไปทางทิศเหนือ 8 กิโลเมตร ย่อมมีตําแหน่งแตกต่างจากการเดินไปทางทิศตะวันออก 6 กิโลเมตร การกล่าวเพียงสั้น ๆ ว่าได้เดินทางไป 8 กิโลเมตร จะไม่สามารถบอก ตําแหน่งสุดท้ายได้ถ้าไม่ทราบทิศของการเดิน ตําแหน่งที่เปลี่ยนไปนี้เราเรียกว่า การกระจัด (Displacement) ซึ่ง เรียกปริมาณที่มีทั้งขนาด (Magnitude) และทิศทาง (Direction) ว่า ปริมาณเวกเตอร์ (Vector quantity) เช่น ความเร็ว ความเร่ง แรง โมเมนต์ ฯลฯ ส่วนปริมาณที่มีเฉพาะขนาดเพียงอย่างเดียวจะเรียกว่า ปริมาณสเกลาร์

(Scalar quantity) เช่น มวล ปริมาตร ความหนาแน่น ความดัน อุณหภูมิ อัตราเร็ว อัตราเร่ง ฯลฯ การคํานวณทาง คณิตศาสตร์ของปริมาณสเกลาร์จะเหมือนกับการคํานวณทั่วไป ส่วนการคํานวณปริมาณเวกเตอร์ จะต้องคํานึ่งถึง
ทิศทางของปริมาณนั้นด้วย จึงเรียกการคํานวณแบบนี้ว่า พีชคณิตเวกเตอร์ (Vector algebra) ซึ่งจะกล่าวอย่าง ละเอียดดังต่อไปนี้
1.1.1 ปริมาณสเกลาร์ (Scalar quantity) ปริมาณสเกลาร์ คือ ปริมาณที่มีแต่ขนาดเพียงอย่างเดียว ไม่มี
ทิศทาง ตัวอย่าง เช่น เวลา อุณหภูมิประจุไฟฟ้า พลังงาน และปริมาตร มวล ระยะทาง อัตราเร็ว อัตราเร่ง เป็นต้น
ดังนั้นปริมาณสเกลาร์จึงเป็นปริมาณต่าง ๆ ที่บอกแต่เพียงขนาดเพียงอย่างเดียวก็เป็นที่เข้าใจได้อย่างสมบูรณ์ได้
1.1.2 ปริมาณเวกเตอร์ (Vector quantity) ปริมาณเวกเตอร์ คือ ปริมาณที่มีทั้งขนาดและทิศทาง ซึ่งอาจ เขียนแทนด้วยลูกศร โดยความยาวลูกศรจะแสดงขนาดและหัวลูกศรแสดงทิศทางของเวกเตอร์นั้น ๆ นอกจากนี้เรา
ยังสามารถเขียนเวกเตอร์ได้ โดยการกําหนดขนาดเวกเตอร์ด้วยตัวอักษรโรมันที่มีหัวลูกศรกํากับ

เวกเตอร์ (vector)

เวกเตอร์เป็นเครื่องมือทางคณิตศาสตร์อย่างหนึ่ง ซึ่งดูเหมือนไม่มีความจำเป็นแตเป็นเครื่องมืออย่างแรกที่ต้องใช้  อย่างไรก็ตามในการศึกษาทางฟิสิกส์เวกเตอร์เป็นเครื่องมือที่มีความสำคัญ  เพื่อช่วยในอำนวยความสะดวกในการคำนวณ

2.1      ระบบพิกัด (แกนอ้างอิง)

ระบบพิกัดมีความสำคัญเพื่อช่วยในการวัดมีความหมาย  เช่นอีก 800 m ถึงอาคารวิทยาศาสตร์เป็นการบอกที่ไม่สมบูรณ์  เนื่องจากไม่ทราบว่าเริ่มต้นที่ตำแหน่งใด

ดังนั้นในการกำหนดระบบพิกัดต้องทราบ

ก.     จุดเริ่มต้น

ข.     ชนิดของระบบพิกัด (พิกัดฉาก ; พิกัดเชิงขั้ว ; พิกัดทรงกระบอก)

ค.     ทิศตามแกน

สมบัติการบวกในระนาบ

1. u + v เป็นเวกเตอร์ในระนาบ สมบัติปิด
2. u + v = v + u สมบัติการสลับที่
3. u + (v + w) = (u + (v) + w สมบัติการเปลี่ยนกลุ่มได้
4. มี 0 โดยที่ 0 + u = u + 0 = u สมบัติการมีเอกลักษณ์
5. สำหรับทุก ๆ u จะมี -u โดยที่ -u + u = 0 = u + (-u) สมบัติการผกผัน
6. ถ้า u = v แล้ว w + v = w + u สมบัติการบวกด้วยเวกเตอร์ที่เท่ากัน

กราฟแสดงผลบวก u + v

ให้
u = ai + bj
v = ci + dj
u + v = (a + c)i + (b + d)j
u – v = (a – c)i + (b – d)j

เวกเตอร์ศูนย์

1. เวกเตอร์ศูนย์ 0 (0) คือเวกเตอร์ที่มีขนาดศูนย์หน่วย
2. จุดเริ่มต้นและจุดสิ้นสุดของเวกเตอร์ศูนย์เป็นจุดเดียวกัน

การคูณเวกเตอร์ด้วยสเกลาร์

ให้เวกเตอร์ u จะเขียน 2u ได้ 2u = u + u

สมบัติการคูณเวกเตอร์ด้วยสเกลาร์

ให้ u และ v เป็นเวกเตอร์ใด ๆ ในระนาบ a และ b เป็นจำนวนจริง
1. au เป็นเวกเตอร์ในระบบ สมบัติปิด
2. a(bu) = (ab)u สมบัติการเปลี่ยนกลุ่ม
3. (a + b)u = au + bu สมบัติการแจกแจง
4. a(u + v) = au + av สมบัติการแจกแจง
5. 1u = u
6. ถ้า au = 0 แล้ว a = 0 หรือ u = 0

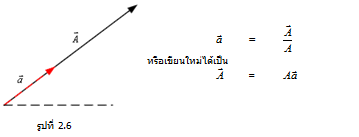
เวกเตอร์หนึ่งหน่วย (Unit vector)

เวกเตอร์หนึ่งหน่วย คือ เวกเตอร์ที่มีขนาดเท่ากับ 1

มองภาพเห็นไหม ยกตัวอย่างให้เห็นภาพชัดเจน

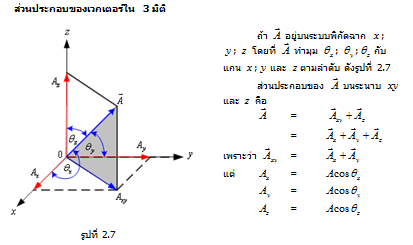
ส่วนประกอบของเวกเตอร์

เวกเตอร์หนึ่งหน่วย คือเวกเตอร์ที่มีขนาด 1 หน่วย และมีทิศทางตามเวกเตอร์ที่พิจารณา เช่น ให้ เป็นเวกเตอร์ที่มีขนาดเท่ากับ และ เป็นเวกเตอร์หนึ่งหน่วย ที่มีทิศเดียวกับเวกเตอร์ ดังรูป

ดังนั้นในระบบพิกัดแกนมุมฉาก เวกเตอร์หนึ่งหน่วยแทนด้วย

มีขนาด 1 หน่วยทิศตามแกน X

มีขนาด 1 หน่วยทิศตามแกน Y

มีขนาด 1 หน่วยทิศตามแกน Z

โดยเวกเตอร์ทั้งสามตั้งฉากซึ่งกันและกัน และเวกเตอร์ทั้งสามจะเรียงกันในทิศทวนเข็มนาฬิกา

จากตัวอย่างที่ 2.3  คำตอบที่ได้สามารถเขียนใหม่ได้เป็น เป็นการเขียนในรูปแบบมาตรฐานซึ่งมีความสะดวกมากเมื่อนำไปใช้ในการบวกและการคูณเวกเตอร์

รูปแแบบทั่ว ๆ ไปของเวกเตอร์เขียนได้ดังนี้ เมื่อ คือส่วนประกอบบนแกน ของ  ; คือส่วนประกอบบนแกน ของ ; คือส่วนประกอบบนแกน ของ เป็นเวกเตอร์ใน 3 มิติ

ผลคูณเชิงสเกลาร์

ผลคูณเชิงสเกลาร์ของเวกเตอร์ หรือภาษาอังกฤษคือ dot product  คือการนำเวกเตอร์มาดอทกันผลลัพธ์จากการนำเวกเตอร์มาดอทกันนี้จะเป็นสเกลาร์หรือว่าตัวเลข  เรามาดูนิยามของมันเลยครับ