กฎเกณฑ์เบื้องต้นเกี่ยวกับการนับ ความน่าจะเป็น (Probability) -ติวเลขความน่าจะเป็น ม.5 ออนไลน์

กฎเกณฑ์เบื้องต้นเกี่ยวกับการนับ

กฎข้อที่ 1

ถ้างานแรกมีวิธีทำได้  n₁ วิธี ในแต่ละวิธีที่เลือกทำงานอย่างแรกมีวิธีที่จะทำงานอย่าง 2 ได้ n₂วิธี และในแต่ละวิธีที่ทำงานอย่างแรกและอย่างที่สอง มีวิธีที่จะทำงานอย่างที่ 3 ได้วิธี n₃ จำนวนทั้งหมดที่จะเลือกวิธีทำงาน k อย่าง เท่ากับ n₁n₂…n_k  วิธี

ตัวอย่างที่ 1 การแต่งกายของดำรงหน่งชุดประกอบด้วย เสื้อ กางเกง และรองเท้าถ้าดำรง มีเสื้อ 5 ตัว กางเกง 3 ตัว  และรองเท้า 2 คู่ ดำรงจะเลือกแต่งกายได้ต่างๆกิ่ชุด

วิธีทำ การแต่งกายของดำรงประกอบด้วย 3 ขั้นตอน คือ

ขั้นตอนที่ 1 เลือกสวมกางเกงซึ่งเลือกได้ 3 วิธี และในแต่ละวิธีทำในขั้นตอนที่ 1 ยังสามารถเลือกทำงาน ในขั้นตอนที่ 2 คือ สวมเสื้อได้อีก 5 วิธีและในแต่ละวิธีที่เลือกทำงาน

ในขั้นตอนที่ 1 และ 2 ยังสามารถเลือกทำงาน ในขั้นตอนที่ 3 คือ สวมรองเท้าได้อีก 2 วิธี

ดั้งนั้น จำนวนวิธีทั้งหมดที่ทำกิจกรรมนี้เสร็จสิ้น    3×5×2 =30 วิธี

นั่นคือ ดำรงสามารถเลือกแต่งกายได้ 30 ชุด

กฎข้อที่ 2

ถ้ากิจกรรมอย่างหนึ่งสามารถทำกิจกรรมเสร็จสิ้นได้ k แบบโดยที่แต่ละแบบทำเสร็จสิ้นได้ n₁n₂…n_k   วิธี ดั้งนั้นจำนวนทั้งหมดที่ทำกิจกรรมนี้เสร็จสิ้นได้ทั้งสิ้น n₁n₂…n_k  วิธี

ตัวอย่าง นายดำมีเสื้อ  2  ตัว  สีต่างกัน  และกางเกง  3  ตัว  สีต่างกัน  จงหาจำนวนวิธีทั้งหมดที่นายดำสวมเสื้อและกางเกงเป็นชุดต่าง ๆ กัน

วิธีคิด       นายดำมีวิธีเลือกสวมเสื้อได้  2   วิธี

เลือกสวมกางเกงได้   3   วิธี

ดังนั้น  นายดำมีวิธีสวมเสื้อและกางเกงเป็นชุดต่าง ๆ กันได้  (2)(3)  =  6  วิธี

อาจใช้แผนภาพต้นไม้ในการหาคำตอบได้ดังนี้

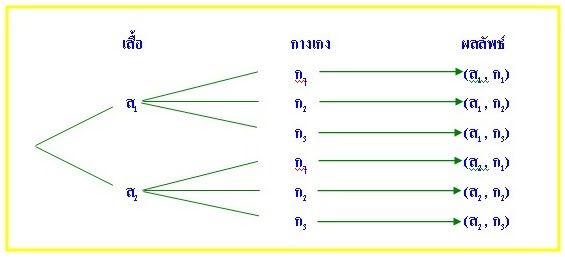
จากแผนภาพต้นไม้  จะได้ว่าจำนวนวิธีทั้งหมดที่นายดำเลือกสวมเสื้อและกางเกงเป็นชุดต่าง ๆ กันเท่ากับ  6  วิธี

หลักการนับ

หลักการบวก

ถ้าการทำงานหนึ่งมีวิธีการทำงาน k วิธี คือ วิธีที่ 1 ถึงวิธีที่ k โดยที่

การทำงานวิธีที่ 1 มีวิธีทำ n₁  วิธี

การทำงานวิธีที่ 2 มีวิธีทำ n₂  วิธี

:                               :

การทำงานวิธีที่  k มีวิธีทำ n_k  วิธี

และวิธีการทำงานแต่ละวิธีแตกต่างกัน แล้วจำนวนวิธีทำงานนี้เท่ากับ n₁+n₂+…+n_k วิธี

ตัวอย่าง นักเรียน 3 คนต้องการเข้าและออกห้องห้องหนึ่งซึ่งมีประตู 3 บาน โดยนักเรียนคนที่ 1 เข้าและออกโดยใช้ประตูบานเดียว นักเรียนคนที่ 2 เข้าและออกโดยไม่ใช้ประตูบานเดิม และนักเรียนคนที่ 3 เข้าและออกโดยใช้ประตูบานใดก็ได้ จงหาจำนวนวิธีที่นักเรียนทั้ง 3 คนเข้าและออกห้องนี้

วิธีทำ    นักเรียนคนที่ 1 มีวิธีเข้าและออกได้ 3 วิธี

นักเรียนคนที่ 2 มีวิธีเข้าและออกได้ 6 วิธี

นักเรียนคนที่ 3 มีวิธีเข้าและออกได้ 9 วิธี

ดังนั้น วิธีที่นักเรียนทั้ง 3 คนเข้าและออกห้องนี้มีทั้งหมด 3+6+9 = 18 วิธี

หลักการคูณ

ถ้าการทำงานอย่างหนึ่งประกอบด้วยการทำงาน k ขั้นตอน คือ ขั้นตอนที่ 1 ถึงขั้นตอนที่ k ตามลำดับ โดยที่

การทำงานขั้นตอนที่ 1 มีวิธีทำ n₁ วิธี

การทำงานขั้นตอนที่ 2 มีวิธีทำ n₂ วิธี

การทำงานขั้นตอนที่ 3 มีวิธีทำ n₃ วิธี

:                                      :

การทำงานขั้นตอนที่ k มีวิธีทำ n_k วิธี

และวิธีการทำงานแต่ละวิธีแตกต่างกัน แล้วจำนวนวิธีการทำงานนี้เท่ากับ n₁n₂n₃…n_k วิธี

ตัวอย่าง บริษัทผลิตเสื้อผ้าสำเร็จรูปแห่งหนึ่งผลิตเสื้อ 6 แบบ กางเกง 5 แบบและเนคไท 4 แบบ ถ้าจะจัดแต่งตัวให้กับหุ่นเพื่อนำไปโชว์หน้าร้าน จะสามารถแต่งเป็นชุดต่างๆกันได้กี่ชุด

วิธีทำ  ในการแต่งตัวให้กับหุ่นมี 3 ขั้นตอน คือ

ขั้นตอนที่ 1 เลือกเสื้อได้ 6 วิธี

ขั้นตอนที่ 2 เลือกกางเกงได้ 5 วิธี

ขั้นตอนที่ 3 เลือกเนคไทได้ 4 วิธี

ดังนั้น วิธีการแต่งตัวให้กับหุ่นทำได้ทั้งหมด 6×5×4 = 120 วิธี

การทดลองสุ่ม

    การทดลองสุ่ม คือ การทดลองซึ่งทราบว่า ผลลัพธ์อาจจะเป็นอะไรได้บ้างแต่ไม่สามารถบอกได้อย่างถูกต้องแน่นอนว่า ในแต่ละครั้งที่ทดลองผลที่เกิดขึ้นจะเป็นอะไรในบรรดาผลลัพธ์ที่อาจเป็นได้เหล่านั้น

    แซมเปิลสเปซ คือ เซตที่มีสมาชิกเป็นผลลัพธ์ที่อาจจะเป็นไปได้ทั้งหมดของการทดลองสุ่ม

ตัวอย่างที่ 1 จากการทดลองสุ่มโดยการทดลองทอดลูกเต๋า 2 ลูก จงหาแซมเปิลสเปซของแต้มของลูกเต๋าที่หงายขึ้น

วิธีทำ เนื่องจากโจทย์สนใจแต้มของลูกเต๋าที่หงายขึ้น ดังนั้นเราจะต้องเขียนแต้มของลูกเต๋าที่มีโอกาสที่จะหงายขึ้นทั้งหมด

แซมเปิลสเปซของการทดลองสุ่ม คือ

S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

 ความน่าจะเป็น

ความน่าจะเป็น ของเหตุการณ์ คือ โอกาสที่จะเกิดเหตุการณ์ที่สนใจเท่ากับเท่าใด

หลักการหาความน่าจะเป็น

ให้ S เป็นแซมเปิลสเปซ ซึ่งแต่ละผลลัพธ์ใน S มีโอกาสเกิดขึ้นเท่าๆกัน E เป็นสับเซตของ S ให้ P(E) เป็นสัญลักษณ์แทน ความน่าจะเป็นของเหตุการณ์ E เราสามารถหา P(E) ได้ดังนี้

ตัวอย่าง กล่องใบหนึ่งมีลูกแก้วสีขาว 3 ลูก สีแดง 2 ลูก หยิบลูกแก้วจากกล่อง 2 ลูก

จงหาเหตุการณ์ที่จะได้ลูกแก้วสีขาว 1 ลูก สีแดง 1 ลูก

เนื่องจากเราสนใจแซมเปิลสเปซของลูกแก้วแต่ละลูกที่ถูกหยิบขึ้นมา ดังนั้นเราให้ ข1 , ข2 , ข3 เป็นลูกแก้วสีขาว 3 ลูก และ ด1 , ด2 เป็นลูกแก้วสีแดง 2 ลูก แซมเปิลสเปซ S = { ข1ข2 ,ข1ข3 , ข1ด1 ,ข1ด2, ข2ข3 , ข2ด1 , ข2ด2 , ข3ด1 , ข3ด2 , ด1ด2 } ให้ A เป็นเหตุการณ์ที่ผลลัพธ์เป็นลูกแก้วสีขาว 1 ลูก และสีแดง 1 ลูก เหตุการณ์ A = { ข1ด1 , ข1ด2 , ข2ด1 , ข2ด2 , ข3ด1, ข3ด2 }

ตัวอย่าง ความน่าจะเป็นที่ A เรียงเป็นตัวแรก จากการเรียงตัวอักษร 2 ตัวจากอักษร 3 ตัว คือ A , B และ C

S = { AB , BA , AC , CA , BC , CB }

E = { AB , AC }

P(E) = 2/6

นั่นคือ ความน่าจะเป็นของเหตุการณ์ที่ A เรียงเป็นตัวแรก = 2/6