การคำนวนหาดีเทอร์มิแนนท์-เมทริกซ์ ม.ปลาย

ดีเทอร์มิแนนต์เมทริกซ์มิติ 2×2

รูปสี่เหลี่ยมด้านขนานจากเมทริกซ์มิติ 2×2 เพื่ออธิบายค่าของดีเทอร์มิแนนต์

กำหนดให้เมทริกซ์มิติ 2×2

จะมีดีเทอร์มิแนนต์เท่ากับ  det(A)= (ab-bc) ซึ่งแปลความหมายได้ว่า เป็นการหาพื้นที่ของรูปสี่เหลี่ยมด้านขนานซึ่งมีจุดยอดอยู่ที่ (0, 0), (a, b), (a+c, b+d), และ (c, d) เมื่อเมทริกซ์นั้นมีสมาชิกเป็นจำนวนจริงพื้นที่ที่คำนวณได้จากดีเทอร์มิแนนต์เหมือนกับพื้นที่ในเรขาคณิต แต่ต่างกันตรงที่ผลลัพธ์จากดีเทอร์มิแนนต์สามารถเป็นค่าติดลบได้ ถ้าจุดยอดดังกล่าวเรียงลำดับตามเข็มนาฬิกา

ดีเทอร์มิแนนต์เมทริกซ์มิติ 3×3

กำหนดให้เมทริกซ์มิติ 3×3

ด้วยการกระจายลาปลัส (หรือการกระจายโคแฟกเตอร์) บนแถวแรกของเมทริกซ์ เราจะได้

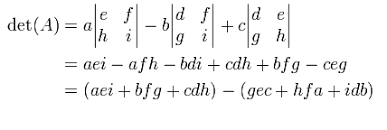
ซึ่งสูตรนี้สามารถจำได้จากการนำผลบวกของผลคูณของสมาชิกสามตัวในแนวเฉียงลง ลบด้วยผลบวกของผลคูณของสมาชิกสามตัวในแนวเฉียงขึ้น (ลงบวก ขึ้นลบ) โดยคัดลอกสองหลักแรกไปต่อท้ายเมทริกซ์เดิม

โปรดทราบว่าวิธีลัดนี้ไม่สามารถใช้กับเมทริกซ์ที่มีมิติสูงกว่านี้ได้

ดีเทอร์มิแนนต์ของเมทริกซ์จัตุรัสทั่วไป ดีเทอร์มิแนนต์ของเมทริกซ์จัตุรัสทั่วไปสามารถคำนวณได้จากการกระจายลาปลัสบนแถวหรือคอลัมน์หนึ่งๆ ซึ่งมีประสิทธิภาพสำหรับเมทริกซ์มิติน้อย ดีเทอร์มิแนนต์จากสูตรของลาปลัสโดยพิจารณาบนแถวที่ iคำนวณได้จาก

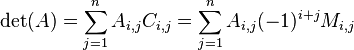
เมื่อ  คือไมเนอร์ (minor) บนแถวที่ i หลักที่ j ของเมทริกซ์ A นั่นคือค่าของดีเทอร์มิแนนต์ของเมทริกซ์ย่อยที่ตัดสมาชิกแถวที่ i หลักที่ j ออกไปทั้งหมด ส่วน  คือโคแฟกเตอร์(cofactor) บนแถวที่ iหลักที่ j ของเมทริกซ์ A ซึ่งมีค่าเท่ากับ  คูณด้วยไมเนอร์